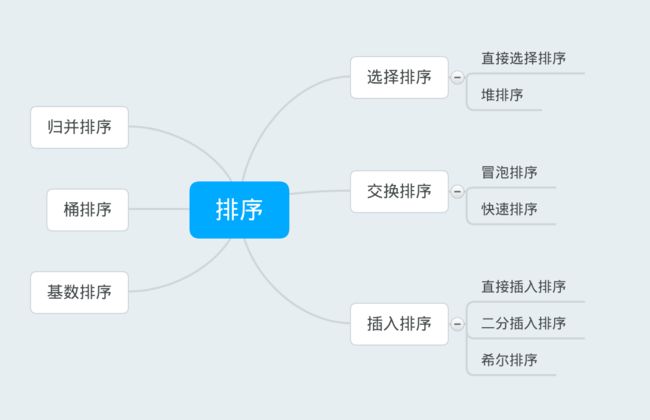
计算机中的排序无处不在,支付宝账单是按照日期默认排序的,微信好友名单是按照姓名首字母排序的。对于能够在主存中完成全部排序内容运算的属于内部排序,当数据量大到需要利用磁盘辅助完成排序的操作属于外部排序。排序大致可以分为以下这几种:
排序算法的逻辑其实很简单,但是不知道为什么,总是记不住,几种排序都能搞混?这是什么鬼?死记硬背呗,总结一下,多重复几次,就可以了!
选择排序法
直接选择排序
首先拿第一个数依次和后面的 n-1 个数进行比较,如果某个数小于第一个数,则和第一个数互相交换,交换后的数继续作为第一个数,直到最后一个元素结束,这称之为第一趟。从这里可以看出,第一趟找出了最小的第一个元素。后面的 n-1 趟以此类推,即可对所有数据排序。
public static void selectSort(int[] data){
int n = data.length;
// 依次进行 n-1 趟比较,找出第 i 小的数放到第 i 个位置
for(int i=0;i data[j])
swap(data,i,j);
}
}
}
以上直接选择排序的时间复杂度为O(n2),空间复杂度为O(1),是不稳定的。这里的稳定指的是相同大小的数排序前和排序后的相对关系不会改变。如例子:new int[]{10,23,45,61,10,2}
但仍然不够好,直接选择排序的逻辑是第 i 趟都要找出一个第 i 小的数据,其实只要找到最小的数据,交换一次就可以了。优化后的程序如下:
public static void selectSortOpti(int[] data){
int n = data.length;
// 依次进行 n-1 趟比较,找出第 i 小的数放到第 i 个位置
for(int i=0;i data[j])
minIndex = j;
}
// 这样可以减少交换次数
if(minIndex != i)
swap(data,i,minIndex);
}
}
堆排序
首先要明白堆的概念,如果将一组数据将其按照原本顺序以完全二叉树的结构构造成树形的结构的话。对这个完全二叉树的任何一个子树中的父节点一定大于其左右子节点,那么就可以称之为大顶堆,反之则为小顶堆。
以大顶堆为例,首先要建堆,然后经这个堆的根节点与最后面的元素交换。第一次建堆就是将第一大的数放到最后一个位子,第二次就是将第二大的数放到倒数第二个位置。堆排序建堆的过程一直在选择,所以它本质上是一种选择排序。
至于如何建堆呢?从最后一个非叶子节点开始,比较该节点和它的两个子节点的大小,将最大的数放在这个子树的根节点位置。知道整个树的根节点,至此完成了大顶堆的建立。
public static void heapSort(int[] data) {
int arrayLength = data.length;
//循环建堆
for(int i=0;i=0;i--) {
//k保存当前正在判断的节点
int k = i;
//如果当前k节点的子节点存在
while(k*2+1 <= lastIndex) {
//k节点的左子节点的索引
int biggerIndex = 2*k +1;
//如果biggerIndex小于lastIndex,即biggerIndex+1
//代表k节点的右子节点存在
if(biggerIndex < lastIndex) {
//如果柚子节点的值较大
if(data[biggerIndex] < data[biggerIndex+1]) {
//biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
//如果k节点的值小于其较大子节点的值
if(data[k] < data[biggerIndex]){
//交换他们
swap(data,k,biggerIndex);
//经biggerIndex赋值给k,开始while循环的下次循环
//重新保证k节点的值大于其左、右子节点的值
k = biggerIndex;
}else {
break;
}
}
}
}
交换排序
为什么叫做交换排序呢?是因为这种排序算法会交换数据吗?可是上面的选择排序也进行了数据交换啊?哈哈,这样想就狭隘了,任何排序必然都一定免不了交换数据的,毕竟你要重新排列顺序。
称之为交换排序是因为它大部分的操作都是在交换数据,上面两种排序算法之所以被归纳为选择排序,是因为它大部分的操作都是在不断地选择。
冒泡排序
首先拿第一个数和第二个数比较,如果第一个数大于第二个数,则交换两个数据。再拿第二个数据和第三个数据相比较,以此类推,直到比较到最后一个元素。这称之为一趟,第一趟能够将最大的数一路交换到最后一位。连续进行 n-1 趟,全部数据排序完成。
public static void bubbleSort(int[] data){
int n = data.length;
for(int i = 0;i < n-1;i++){
boolean flag = true;
for(int j = 0;j < n-1-i;j++){
if(data[j] > data[j+1]){
swap(data,j,j+1);
flag = false;
}
}
if(flag) //说明未完成 n-1 趟就已经排好序了
break;
}
}
时间复杂度为O(n2),空间复杂度为O(1),冒泡排序是稳定的。
快速排序
快速排序的的思想就是选出第一个数作为分界值,然后通过交换数据,使得小于分界值的数位于左边,大于分界值的数位于右边。然后通过递归调用不断划分,知道最后每个分区只剩下一个数据,则结束。
使用两个下标 i 和 j ,i 从左往右移动,找到大于基数的数就停下来,j 从右往左移动,找到小于 j 的数就停下来。把 i 和 j 对应的数互相交换,前提当然是建立在 i < j 的基础上的啦。
private static void subQuickSort(int[] data,int start,int end){
if(start < end){//需要排序
int base = data[start];//选定的基数
int i = start;//i从左往右搜索大于基数的数
int j = end+1;//j从右往左搜索小于基数的数
while(true){
//当i指向的值小于base时,i需要不停往右移动
while(istart && data[--j] >= base);
if(i < j)
swap(data,i,j);
else
break;
}
swap(data,start,j);//将最后j指向的值与基数交换
subQuickSort(data,start,j-1);//递归左边子序列
subQuickSort(data,j+1,end);//递归右边子序列
}
}
递归版快速排序的时间和空间复杂度都是O(logn),这里虽然没有用到新的存储空间,但是以为递归需要使用到栈,每调用一次就增加一个栈帧空间。
插入排序
插入排序顾名思义,就是大部分时候都是在做插入操作啦。
直接插入操作
对于一个有 n 个元素的序列,需要进行 n-1 趟插入数据才可以完成整个排序过程。第一趟直接将第二个元素插入前面已经由第一个元素构造的有序子序列中,第二趟就直接将第三个元素插入前面的有序子序列,知道第 n 个元素插入完成。
public static void insertSort(int[] data){
int n = data.length;
for(int i=1;i0 && data[j] < data[j-1]){
data[j] = data[j-1];//后移一位
j--;
}
data[j] = temp;//找到合适位置存放了
}
}
直接插入排序的时间复杂度为O(n2),空间复杂度为O(1)。如果遇到相同大小的数,放在它的后面,则直接插入排序是稳定的。
二分插入排序
上述直接插入排序的算法在有序子序列中寻找插入位置时,采用的是从右往左依次遍历的方法。实际上这忽略了子序列已经是有序的情况,这里完全可以利用这种特性,采用二分查找来快速确定插入位置。
public static void binaryInsertSort(int[] data){
int n = data.length;
for(int i=1;i data[mid])
low = mid + 1;
else
high = mid -1;
}
//已经找到需要插入元素的位置low了
for(int j = i;j>low;j--){
data[j] = data[j-1];//依次后移,空出一个位置
}
data[low] = temp;
}
}
时间复杂度仍然是O(n*n),但是比直接插入排序还是快了很多的。
二分归并排序
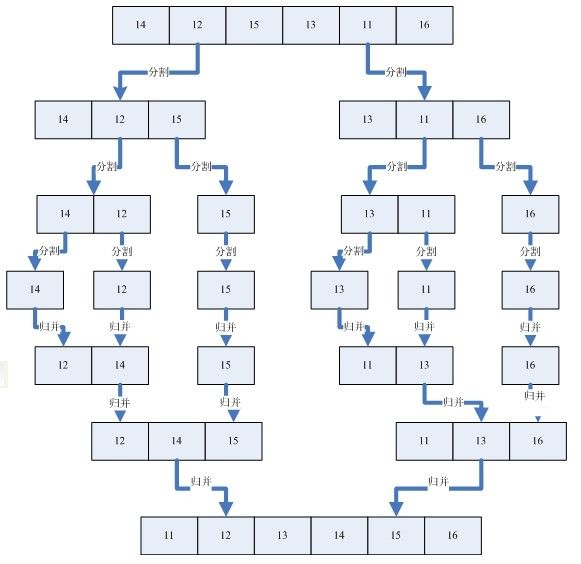
二分归并排序的基本思想就是将两个有序的序列合并到一个新的有序序列中,以此就可以完成整个序列的排序过程。
那有序序列从哪里来呢?这就需要使用递归去不断的分解,直到子序列只剩下一个数,那这个序列自然就是有序序列了。具体的递归分解以及合并过程如下图所示
/**
* 归并排序
*/
public static void mergeSort(int[] data){
mergesort(data,0,data.length-1);
}
private static void mergesort(int[] data,int left,int right){
if(left < right){
int center = (left + right)/2;
mergesort(data,left,center);
mergesort(data,center+1,right);
merge(data,left,center,right);
}
}
private static void merge(int[] data,int left,int center,int right){
int[] tempArr = new int[data.length];
int mid = center+1;
int tempIndex = left;//tempArr数组的下标
int temp = left;
while(left <= center && mid <= right){
if(data[left] <= data[mid]){
tempArr[tempIndex++] = data[left++];
}else{
tempArr[tempIndex++] = data[mid++];
}
}
//将未完成的放到tempArr中
while(left <= center){
tempArr[tempIndex++] = data[left++];
}
while(mid <= right){
tempArr[tempIndex++] = data[mid++];
}
//将中间数组的内容复制回原数组
while(temp <= right){
data[temp] = tempArr[temp++];
}
}