Python递归函数的运用
什么是递归函数?
在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数。
意义:通过一定的“基”,并按照某种规则达到重复的效果
递归函数实现斐波那契数列
斐波那契数列的定义:
斐波那契数列指的是这样一个数列 :
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368…
这个数列从第3项开始,每一项都等于前两项之和。
关键点在于每一项都等于前两项之和。意思是:如果我们想计算这个数列的某一个数,我们得先知道这个数的前两个数是多少。假设这个数的前两个数分别为a, b.
那么这个‘基’就可以得出来了:a和b。
那么这个数列遵循的规则也可以得出来了:a+b
那么我们用函数来求斐波那契数列中的某一个数吧。(不用递归)
def fib(n):# n为数列中的第几个数
if n == 1 or n == 2:
return 1
a, b = 1, 1
n -= 2
while n > 0:
a, b = b, a + b
n -= 1
return b
使用递归。
def fib(n):
if n == 1 or n == 2:
return 1
return fib(n-1) + fib(n-2)
使用递归函数实现汉诺塔
直接上数学模型
有三根相邻的柱子,标号为1,2,3,柱子1上从下到上按金字塔状叠放着n个不同大小的圆盘,要把所有盘子一个一个移动到柱子3上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。
让我们来寻找这个数学模型中的‘基’和规则吧。
我们发现每一次的移动数等于上一次的移动数×2+1。那么我们是不是可以假设每一次的汉诺塔的移动都在一定程度上基于上一次的移动。我们用具体事例验证下。
因为n=1与n=2之间太过于简单,很难找到明显的规律。所以我们比对n=2与n=3
当n=3时
基于上述的发现(每一次的移动数等于上一次的移动数×2+1)我们将这一次的移动分为三个部分。因为移动是有一定规律的,所以我们只能有三种分法:(3,3,1),(1,3,3),(3,1,3)
通过比对所有的移动方法,我们可以发现最中间的那一次移动都是“1 --> 3”。所以我们确定分法为(3,1,3)
我们将n=3与n=2进行比较
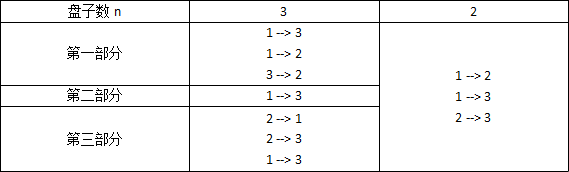
我们会发现:将n=2中的柱子2、3进行交换就可以得到n=3的第一部分,将n=3中的柱子1、2交换就可以得到n=3的第三部分。
同理去推n=1与n=2、n=4与n=3之间的关系,我们会得到同样的结论。
而且n=1时的移动(1 --> 3)还给了我们一个明确的信息:我们移动的最终目的都是将所有盘子从柱子1移动到柱子3。
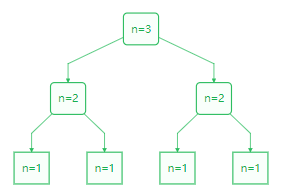
因为‘基’是n=1,所以有:
def hano(n, a, b, c):
if n == 1:
print(a, '-->', c)
根据规则可以写出:
hano(n - 1, a, c, b)
print(a, '-->', c)
hano(n - 1, b, a, c)
再优化一下:
def hano(n, a, b, c):
if n == 1:
print(a, '-->', c)
return
hano(n - 1, a, c, b)
print(a, '-->', c)
hano(n - 1, b, a, c)
a, b, c = "1", "2", "3"
print("这是汉诺塔游戏!")
n = int(input("请输入汉诺塔的层数:"))
hano(n, a, b, c)
给大家留个小题:
有三根相邻的柱子,标号为1,2,3,柱子1上从下到上叠着n个盘子,叠的方式为:一黑一白交替相叠,白色的总在最下面。要把所有盘子一个一个移动到柱子3上,使最终的柱子3呈现的结果为:白色盘子全部在下面,黑色盘子全部在上面。怎样移动使步骤最少。大家可以试试用递归的方法模拟。
上述只是小弟的一点愚见,代码并没有经过大量测试,可能有误,欢迎各位大佬在评论区里;留言指出。感谢大家的阅读