NAACL | 通过对抗性修改，探究链接预测的鲁棒性和可解释性

作者 | 苏祥

审稿 | 潘小琴

单位 | 湖南大学

今天为大家带来一篇美国加州大学欧文分校发表在NAACL 2019上的一篇论文。在本文中，作者提出了对链路预测模型的对抗性修改：识别出添加到知识图谱中，或者从知识图谱中删除的事实，这些事实能够在模型经过重新训练后更改对目标事实的预测。利用对图的删除，作者识别出对预测链接最有影响的事实来研究可解释性；利用对图的添加，评估模型的鲁棒性。同时，作者引入了一种有效近似嵌入的方法来估算知识图谱修改的效果。

1

简介

知识图谱是结构化的语义知识库，通过使用符号的形式来描述世界中的各种概念及它们之间的关系。它们的形式通常表示为“头实体-关系-尾实体”的三元组（），我们通常将每一个三元组都称为一个现实世界中的“事实”。现如今，知识图谱在许多实际应用中扮演着重要的角色，但是它通常是不完全的，会缺失许多事实。现有的研究提出了许多嵌入模型，将每个实体和关系嵌入到向量空间中，并利用这些嵌入来预测事实，然而却只有少数研究调查了不同嵌入模型的质量。

在这篇论文中，作者引入对抗性修改的思想，旨在设计一种能够最小程度改变图结构，使得目标事实的预测结果在重新学习后发生变化最大的方法。作者将这个方法统称为通过对抗性图编辑完成鲁棒性和可解释性，简称CRIAGE。

2

通过对抗性图编辑完成鲁棒性和可解释性

2.1、删除事实（CRIAGE-Remove）

2.2、添加事实（CRIAGE-Add）

3

高效识别修改

在对知识图谱进行对抗性修改时也有许多关键性的挑战。首先，评估改变知识图谱对目标事实得分的影响是非常昂贵的，因为我们需要通过在新图上重新训练模型来更新嵌入项；其次，因为有许多候选事实可以添加到知识图谱中，使用基于搜索的方法来识别最有潜能的候选事实也很昂贵。

于是，针对上述挑战，作者提出了相应的解决算法。（1）逼近更改图形对目标预测的影响，（2）使用连续优化对潜在修改进行离散搜索。

3.1、影响的一阶近似

3.2、持续优化搜索

使用上面提供的近似值，在删除观察到的三元组时，我们可以使用暴力枚举的方法来找到对抗三元组，因为此时需要修改的搜索空间通常很小。而如果我们要添加伪造的三元组事实的话，需要在更大的空间中搜索，代价可能非常昂贵。

4

实验

作者通过以下方法评估了CRIAGE：1）将CRIAGE估计值与攻击的实际效果进行比较，2）研究对抗性攻击对评估指标的影响，3）探索其在知识图谱表示的可解释性中的应用，以及4）检测不正确的三元组。

4.1、影响函数（IF）VS CRIAGE

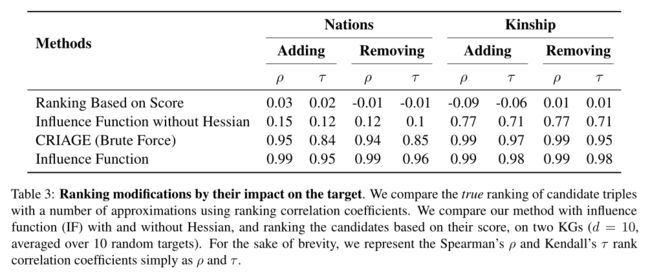
作者采用留一法进行实验，将一个随机目标三元组的所有邻居作为候选修改，每次删除一个，每次重新训练模型，并计算目标三元组分数的精确变化。可以利用分数变化的幅度来对候选三元组进行排序，并将这个确切的排名与预测的排名进行比较：CRIAGE-Remove，有无Hessian矩阵的影响函数（IF），以及原始模型得分（直觉上，模型最有信心的事实将在移除时产生最大的影响）。

从表3可以看出，CRIAGE的性能与影响函数（IF）相当，证明了近似的准确性。影响函数（IF）的精度稍高，是因为它们在所有参数上都使用完整的Hessian矩阵。这种差异对可伸缩性的影响是巨大的。

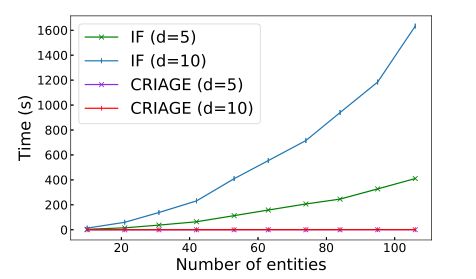
作者展示了IF（影响函数）与CRIAGE由于实体数量变化而产生的时间变化。如图3所示，CRIAGE几乎不受实体数量的影响，而IF则成倍增加。考虑到现实世界中的知识图谱拥有数以万计的实体，这使得使用IF对他们而言并不现实。

4.2、链接预测模型的鲁棒性

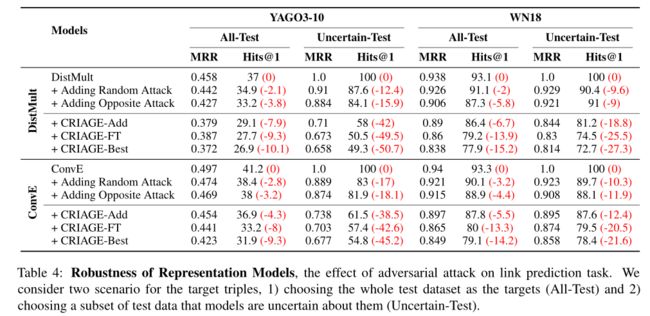
All-Test：表4提供了针对所有测试事实作为目标的攻击结果。CRIAGE-Add优于基线，表明其具有效攻击知识图谱表示形式的能力。

Uncertain-Test：为了更好地理解攻击的影响，作者考虑一个测试三元组的子集：1）模型预测正确；2）其得分与得分最高的阴性样本之间的差异最小。这个“不确定测试”子集包含100个来自每个原始测试集的三元组。在这种情况下，攻击的效率会更高，从而导致指标大幅下降。

4.3、模型的可解释性

为了能够解释为什么预测了链接，作者使用CRIAGE-Remove确定最有影响力的事实。他们不再关注单个预测，而是使用简单的规则提取技术将每个关系的解释汇总到整个数据集上：作者在子图中找到了简单的模式，这些模式围绕目标三元组以及从CRIAGE-Remove中删除的事实，并且有90％以上的时间出现。作者还与DistMult论文中说到的提取规则进行比较。有趣的是，提取的规则包含CRIAGE提供的所有规则，表明CRIAGE可用于准确解释模型。

4.4、查找知识图谱中的错误

直观地说，如果图中有错误，三元组很可能与其邻域不一致，因此模型应该对这个三元组的信任度最小。换句话说，错误的三元组对训练数据的预测影响最小。我们如果要在训练三元组的邻域找到错误的三元组，只要保证在移除某个三元组时，的改变最小。

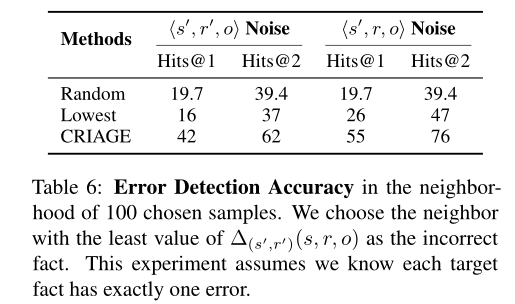
为了评估这个应用程序，作者将随机三元组注入到图中，并使用他们的优化来衡量CRIAGE检测错误的能力。考虑两种类型的错误三元组：1）形式的错误三元组，其中是从所有实体中随机选择的；2）形式的错误三元组，其中和是随机选择的。从观察到的图中选择100个随机三元组，并为每个三元组（在两种情景下的每一个）添加一个错误的三元组到它的邻域中。然后，在对这些噪声训练数据使用DistMult模型重新训练。之后，通过搜索100个事实的邻域来识别错误的三元组。

表6给出了选择对目标影响最小的邻居的结果。当与随机选择一个邻域（Random），或者假设得分最低的事实是不正确的（Lowest）两种基线进行比较时，作者发现CRIAGE在检测错误方面的准确率分别为42%和55%，优于这两种方法。

5

总结

基于分析链路预测模型的鲁棒性和可解释性的需要，作者提出了一种对知识图谱进行对抗性修改的新方法。通过对抗性图形编辑来引入CRIAGE，完善鲁棒性和可解释性：确定要添加到或从KG中移除的改变目标事实预测的事实。CRIAGE使用（1）在添加或删除另一个事实后对任何目标三元组的分数变化的估计，（2）基于梯度的算法来识别最有影响的修改。

代码

https://github.com/pouyapez/criage

参考资料

https://arxiv.org/abs/1905.00563