单源最短路径
在图的应用中,最短路径问题是最常见的,这里介绍并使用java实现两种解决最短路径的算法,分别是Dijkstra算法和Bellman-ford算法。
1、单源最短路径
一个顶点序列i1,i2........ik是图的一条路径,当且仅当边(i1,i2)(i2,i3).........(ik-1,ik)都在图中。如果除了第一个顶点和最后一个顶点之外,其余的顶点均不相同,那么这条路径称为简单路径。以一个源节点s为起始节点到图G中可到达节点的简单路径构成的一棵以s的树就是单源最短路径,树中的任一个节点v,s到v就是图G中s到v的一条最短路径。
为了解决单源最短路径问题,引入松弛技术。对于每个节点v来说,维持一个属性v.d,用来记录从源节点s到节点v的最短路径的上界。称v.d为s到v的最短路径估计,另外依旧使用pi属性来记录发现一个节点的前驱结点。下面是单源最短路径的伪代码:
INITIALIZE-SINGLE-SOURCE(G,s)
for each vertex belong to G.V
v.d=MAX_VALUE //初始距离无穷大
v.pi=NIL //前驱结点为空
s.d=0 //源节点的
RELAX(u,v,w)
if v.d>u.d+w(u,v)
v.d=u.d+w(u,v)
v.pi=u需要注意的是如果如果图中含有这样一个圈:这个圈的权重加起来小于0,那么进行松弛操作时就会一直在这个圈中循环并不断减小路径长度趋近无穷小,这样的圈在单源最短路径中是不允许的。
思想:对所有点进行松弛操作,然后判断是否存在负圈,如果没有,则含有单源最短路径,否则没有。下面是算法的伪代码:
BELLMAN-FORD(G,w,s)
INITIALIZE(G,s)
for i=1to|G.V|-1
for each edge (u,v) belong to G.E
RELAX(u,v,w(u,v))
for each edge(u,v) belong to G.E
if v.d>u.d+w(u,v)
return FALSE
return TRUE思想:Dijkstra算法维护一个顶点集合Q,Q初始时等于G.V,每次从Q中取出一个顶点u并且这个顶点u.d是最小的。对顶点u的出边都进行松弛松弛操作。不断从Q中取出顶点直到Q为空。下面是算法的伪代码:
//单源最短路径Dijkstra算法
DIJKSTRA(G,w,s)
S=null
Q=G.V
while Q!=null
u=EXTRACT-MIN(Q) //从队列中取出一个元素
S=S U {u} //集合S并上u
for each vertex v belong G.Adj[u]
RELAX(u,v,w) //松弛u,v节点算法使用的图的数据结构在另一篇文章数据结构 图的存储邻接矩阵与邻接链表中详细描述,如果需要可以点击查看。
package Algorithm;
import java.util.LinkedList;
/*
* @vamesary
* 11/5/2017
*单源最短路径
*/
import Structure.Graph;
import Structure.Node;
import Structure.LinkList;
public class ShortestPath {
private LinkList [] list;//邻接链表
private int vertex=0;//图的顶点个数
private int [] d; //与源节点s的距离
private int [] pi; //前驱结点
private int source; //源节点
//自己随机生成图
public ShortestPath(int theVertex,int theEdge){
Graph graph=new Graph(theVertex,theEdge,false);
list=graph.getList();
vertex=graph.getVertex();
//System.out.println(graph.toString());
}
//使用现有图构造函数
public ShortestPath(Graph graph){
list=graph.getList();
vertex=graph.getVertex();
//System.out.println(graph.toString());
}
//初始化图方法
public void initialize(int s){
source=s;
d=new int [vertex];
pi=new int [vertex];
for(int i=0;id[uid]+weight){
d[vid]=d[uid]+weight;
pi[vid]=uid;
}
}
//单源最短路径Bellman-Ford算法
public boolean Bellman_Ford(int s){
initialize(s);
int u=0;
while(ud[u]+v.weight)
return false;
v=v.next;
}
u++;
}
return true;
}
//单源最短路径Dijkstra算法
public void Dijkstra(int s){
initialize(s);
LinkedList Q=new LinkedList();
for(int i=0;i";
j=pi[j];
}
str+=j;
}
return str;
}
}
测试:
package Test;
import Algorithm.ShortestPath;
import Structure.Graph;
public class ShortestPathTest {
public static void main(String[] args) {
int [][]array=new int[9][9];
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
array[i][j]=-1;
}
}
array[0][1]=4;array[0][2]=8;
array[1][0]=4;array[1][2]=11;array[1][3]=8;
array[2][0]=8;array[2][1]=11;array[2][4]=7;array[2][5]=1;
array[3][1]=8;array[3][4]=2;array[3][6]=7;array[3][7]=4;
array[4][2]=7;array[4][3]=2;array[4][5]=6;
array[5][2]=1;array[5][4]=6;array[5][7]=2;
array[6][3]=7;array[6][7]=14;array[6][8]=9;
array[7][3]=4;array[7][5]=2;array[7][6]=14;array[7][8]=10;
array[8][6]=9;array[8][7]=10;
Graph graph =new Graph(array,9);
ShortestPath shortestpath=new ShortestPath(graph);
shortestpath.Bellman_Ford(0);
System.out.print("Bellman_Ford算法");
System.out.println(shortestpath);
shortestpath.Dijkstra(0);
System.out.print("Dijkstra算法");
System.out.println(shortestpath);
}
}
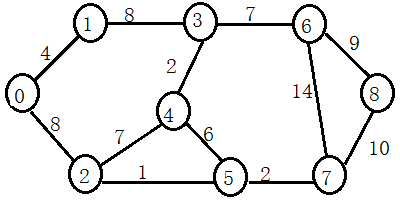
测试用图
Bellman_Ford算法
distance: 0 0
distance: 4 1->0
distance: 8 2->0
distance: 12 3->1->0
distance: 14 4->3->1->0
distance: 9 5->2->0
distance: 19 6->3->1->0
distance: 11 7->5->2->0
distance: 21 8->7->5->2->0
Dijkstra算法
distance: 0 0
distance: 4 1->0
distance: 8 2->0
distance: 12 3->1->0
distance: 14 4->3->1->0
distance: 9 5->2->0
distance: 19 6->3->1->0
distance: 11 7->5->2->0
distance: 21 8->7->5->2->0