本文来自肥宝传说之路,引用必须注明出处!
游戏里面经常用到坐标转换,例如地图、战斗技能等。
一、直角坐标和极坐标的转换
前提条件:
1、两坐标系原点重合
2、两坐标系x轴正半轴重合
3、两坐标系单位长度相同
变量关系:
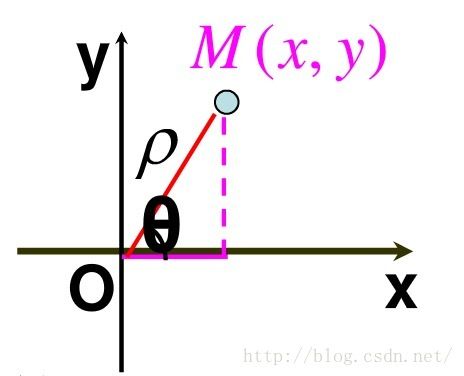
如上图,M的直角坐标为(x,y),极坐标(ρ,Θ)。
由图中关系可以得出
ρ^2 = x^2 + y^2 (勾股定理)
tanΘ = y/x
x = ρ*cosΘ
y = ρ*sinΘ
其他象限的就不证明了,这里不是讲数学的。知道是一样就行了。
代码如下:
#include 二、绝对坐标和相对坐标的转换
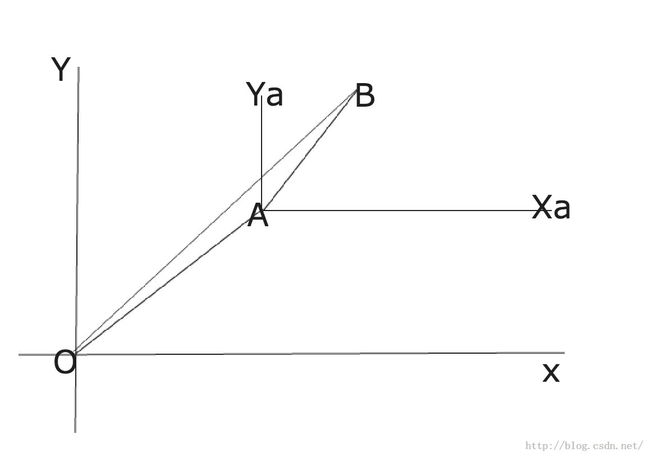
如图中坐标系O和坐标系A,原点分别是O(0,0),A(xa,ya).这个相对坐标系A的x轴和y轴是跟坐标系O的x轴和y轴分别平行的。
对于B(xb,yb)的相对坐标是(xb-xa,yb-ya)
就这么简单。
但是,如果A的坐标轴跟O的不平行呢?看下图
说一下运用的背景,例如怪物A身上有个喷火技能,释放技能的时候,喷出一条火线,在火线上的的玩家都会受到伤害。犹豫在计算机上,直线的范围太小。如果我们只用直线来计算。很可能站在附近便宜一个像素的角色B就逃过的攻击。可以说,这种技能基本上攻击不了其他角色,除了特意攻击的那个。
下图中O为原点。怪物A,角色B/C/D三个,ABCD的绝对坐标都是知道的。怪物A锁定B,向B喷火。(图画得有点不好,大家不要介意)。以喷火路线为相对坐标系的x轴。火线长为L,宽为W。一般来说,B是必然中招的(这都不中招就是有bug了)。相对坐标的x轴,就是向量AB的方向。Y轴垂直于向量AB
这个时候要判断C和D是否也被击中了。
我们先看C的相对坐标。AC是点的距离,再求角CAB就可以得到极坐标,然后用极坐标转换成直角坐标就可以了,
根据余弦定理 BC^2 = AC^2 + AB^2 - 2*AB*BC*cos(角CAB)。
所以cos(角CAB) = (AC^2 + AB^2 - BC^2)/ 2*AB*BC
然后根据上面一提到的极坐标和直角坐标的转换。得出相对坐标xr = AC * cos(角CAB); yr ^2 = AC ^2 + yr ^ 2 ;
(xr,yr)就是相对坐标了。记得BC等于零的时候是不行的。(都重合了还需要计算么?)
再看看实现代码吧:
class CPoint
{
public:
double x;
double y;
}
double computeDistance(CPoint from, CPoint to)
{
return sqrt(pow(to.x - from.x, 2) + pow(to.y - from.y, 2));
}
CPoint Common::changeAbsolute2Relative(CPoint originPoint, CPoint directionPoint, CPoint changePoint)
{
CPoint rePoint;
if (originPoint == directionPoint)
{
rePoint.x = changePoint.x - originPoint.x;
rePoint.y = changePoint.y - originPoint.y;
}
else
{
double a = computeDistance(changePoint, originPoint);
double b = computeDistance(directionPoint, originPoint);
double c = computeDistance(directionPoint, changePoint);
double cosa = (b*b + c*c - a*a) / 2 * b*c;//余弦定理
rePoint.x = a * cosa ;
rePoint.y = sqrt(a*a - rePoint.x*rePoint.x);
}
return rePoint;
}