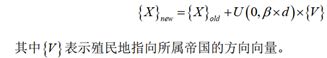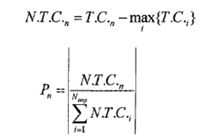快速对帝国竞争算法ICA的了解
帝国竞争算法ICA
帝国竞争算法通过模拟帝国主义殖民竞争机制而建立其数学模型,本质上是基于群体的随机优化搜索方法。
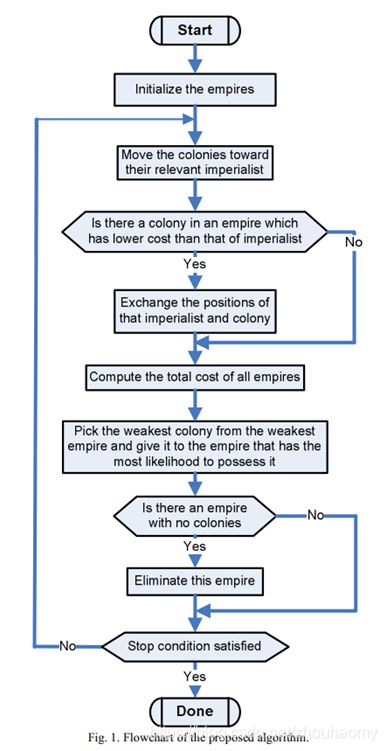
算法流程图:
1. 初始化帝国
对于一个N维的优化问题,国家可以表示成如下形式:
![]()
国家的势力大小通过代价函数来衡量:
![]()
国家的势力和代价函数值成反比,即代价函数值越小,国家势力越大。
具体步骤:
2. 同化与反转机制
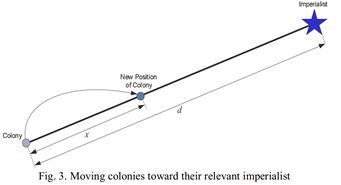
帝国主义国家对殖民地进行改善和思想控制,即同化作用。通过所有殖民地国家向其所属帝国主义国家移动来模拟同化过程。
殖民地向帝国主义国家移动的距离x定义如下:
x ~ U(0,β×d)
其中,β>1,殖民地可以从两个方向朝Imp靠近;d是殖民地和Imp之间的距离,随机变量x服从(0,β×d)上的均匀分布。
同化公式:
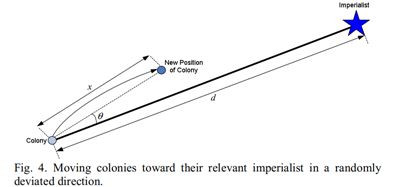
为了在帝国主义国家周围寻找不同的点,扩大寻找范围,增加了一个随机偏离方向θ,定义如下:
θ ~ U(-γ , γ)
其中,0< γ <π。(大多应用中β常取2,γ常取π/4)
殖民地国家向帝国主义国家靠近时,殖民地的位置发生更新,可能出现某个殖民地的代价函数值比帝国主义小的情况,即该殖民地的势力更大,此时,将该殖民地与Imp的角色进行交换,即该殖民地成为该帝国的Imp,而原来的Imp则沦为殖民地。
3. 帝国竞争机制
帝国竞争机制模拟的是现实社会中势力较强的帝国占有并控制势力较弱帝国的殖民地的过程。帝国之间的竞争导致强的帝国变得更强,而弱的帝国逐渐衰败。
具体步骤:
第1步:计算帝国的总代价函数值,即势力大小。帝国主义国家对整个帝国的势力影响较大,而殖民地国家的影响非常小。
帝国总代价公式:
也即是:
第2步:根据各帝国的总代价,选择最弱的帝国中最弱的殖民地作为帝国竞争的对象,势为越大的帝国越有可能占有该殖民地。每个帝国占有最弱殖民地的概率按照如下公式计算:
其中,T.C.n和N.T.C.n分别是第n个帝国的总代价和标准化总代价,Pn是第n个帝国占有殖民地的概率。
第3步
4. 帝国灭亡,合并收敛
帝国之间的竞争,使势力大的帝国通过占有其他帝国的殖民地变得越来越强大,而势力弱的帝国殖民地个数不断减少,当一个帝国丢失所有的殖民地时,帝国覆灭。随着帝国的灭亡,最终剩下一个帝国,此时算法终止。
除了最强大的帝国之外,所有帝国都会崩溃,所有殖民地都将在这个独特的帝国的控制之下。在这个理想的新世界中,所有殖民地将拥有相同的地位和成本,并且将由帝国主义者以与自己相同的地位和成本进行控制。在这个理想的世界中,不仅殖民地之间没有区别,而且殖民地与帝国主义之间也没有区别。在这种情况下,我们结束了帝国主义的竞争并停止了算法。
总结:
帝国竞争算法与PSO、GA相比,收敛速度快、收敛精度高,具有较强的全局收敛性;但由于竞争过程中帝国合并以及帝国覆灭使ICA的帝国个数不断减少,导致群体多样性降低,算法的全局"勘探"能为受影响,易出现"早熟"现象。
帝国竞争算法包含的基本要素:初始国家数目,帝国主义国家数和殖民地数,
帝国竞争年限,帝国主义国家权力(代价函数f、殖民地影响因子ξ),同化系数(β和γ)。
参考文献:
[1] Atashpaz-Gargari E, Lucas C. Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition[C]//2007 IEEE congress on evolutionary computation. Ieee, 2007: 4661-4667.
[2] 郭婉青, 叶东毅. 帝国竞争算法的进化优化[J]. 计算机科学与探索, 2014, 8(4): 473-482.
[3] 郭婉青. 帝国竞争算法的研究与改进[D]. 福州大学, 2014.
[4] Kaveh A, Talatahari S. Optimum design of skeletal structures using imperialist competitive algorithm[J]. Computers & structures, 2010, 88(21-22): 1220-1229.
本人为快速了解帝国竞争算法,查阅了几篇文献所总结。不足之处,还请见谅。