什么是算法?从枚举到贪心再到启发式(下)-终于有人把邻域搜索讲清了!
前言
在上一篇文章中,我们聊了枚举算法和贪心算法,并进行了详细对比,让大家了解了这两个算法的相关特点。相关的传送门如下:
什么是算法?从枚举到贪心再到启发式(上)
今天咱来聊聊启发式算法吧。至于什么是启发式算法,为什么有了枚举和贪心,还要启发式算法。看完这篇文章,相信你就能找到答案哦。
什么是启发式算法?
在上一篇文章中,我们对比分析了枚举法和贪心法的特点。枚举法呢,虽然能求得问题的最优解,但是所花的时间是在是太太太大了。贪心法呢,虽然能在极短的时间内找到一个尚且过得去的解,但是呢,有时候求得的解是在是太low啦。虽然在上次的文章中大家没有很明显看到这一点,因为0-1背包问题还算比较简单,但是在一些复杂的组合优化问题比如vrp问题中,贪心法的弊端就凸显出来了。
所以啊,枚举法时间太长没法用,贪心质量太差,人们就需要另辟蹊径,找到一条既能够得到一个比较优质的解,又能将求解资源控制在一定范围内的社会主义道路。这时候启发式算法就应运而生啦。
说白了,启发式算法就是在一个合理的求解资源范围内(合理的时间,合理的内存开销等)求得一个较为满意的解。该解毫无疑问,是要优于或等于贪心解,有可能达到枚举法求得的最优解。这是怎么做到的呢?下面让我慢慢道来。
注:启发式算法目前主要包括邻域搜索和群体仿生两大类,本篇主要介绍邻域搜索类。同时邻域搜索类会涉及很多概念,我尽量用大白话的语言向大家阐述。因为启发式算法强调的是一个应用,即你拿到问题能设计相应的算法并求解出来。概念只是辅助我们理解这个过程而已。
先从局部搜索说起
大家平常找东西都是怎么找的呢?按照正常人的思路,丢了东西以后我们往往都会先确定一个范围,然后沿着确定的范围进行搜索。这其实就有种局部搜索的味道了。
不过在开始局部搜索前,我们先来了解一个概念,解空间。
问题的解空间是指所有该问题的解的集合,包括可行解和不可行解。
对于算法而言,其本质就是一个搜索寻优的过程。在哪里搜?当然是在解空间里面搜啦。一开始人们的做法是遍历整个解空间进行全局搜索,然后找出问题的最优解。但是渐渐地人们发现,当问题规模增大时,其解空间就会变得很大很大。全局搜索需要的时间和资源是无法接受的。这就像你去华中科技大学游玩的时候丢了身份证,别说是对整个洪山区展开地毯式搜索,光是对我科展开地毯式搜索都够呛。
所以,为了解决这个问题,人们就想出了另一种方式:局部搜索。说白了就是咱不完全遍历解空间了,只挑一部分出来进行遍历,这样就可以大大降低搜索需要的资源,说不定碰巧挑出来的局部中还含有最优解呢。
如上图,局部搜索时如果只搜索蓝色虚线左下的区域,那么就有可能找到最优解。为了提高局部搜索的质量,大部分局部搜索算法都会在搜索的时候不断地抓取多个区域进行搜索,直到满足算法终止条件。
邻域搜索
相信大家肯定存在一个疑问,局部搜索是怎么挑选“局部”的?别急,看完本节邻域搜索的内容,你就understand了。
邻域搜索是基于“邻域”的一类启发式算法,本质还是属于局部搜索的范畴。在此之前我们还是介绍必要的一些概念。
“同学”、“家人”、“邻居”这些概念想必大家已经非常熟悉了。下面我们来看一张有趣的图片:
你,通过血缘关系,可以找到你的家人集合(包括你爸爸、妈妈、爷爷奶奶等);你家,通过地里位置上的距离远近,可以找到你家的邻居集合(隔壁的、对面的、同楼层的);你,通过判断与你是否同一班级,可以找到你同学的集合(同班的就是你同学)。
大家发现没有,上面的示例都是通过某种关联(血缘关系、距离远近等),将一个基准点(比如你、你家)映射到了一个集合(比如你的家人、你家的邻居)上面。
好了我们现在再来看一张图:
上面就是生成一个解的邻域的过程,怎样,是不是跟刚刚的几个例子(图1)有着异曲同工之妙呢?邻域生成的过程(图2)其实也是一样的,只不过是使用了更专业的概念而已。下面我们就来解释下这些概念的含义吧。
概念介绍
邻域
邻域其实就是在邻域结构定义下的解的集合,比如在图2中s1-s6等构成的集合就是s的邻域。它是一个相对的概念,即邻域肯定是基于某个解产生的,比如当前解s的邻域,最优解s_b的邻域等。
邻居解
邻居解是邻域内某个解的称呼。比如在图2中,解s1-s6及其该邻域中任意一个解都可以称为解s的邻居解。很好理解对吧~
邻域结构
邻域结构定义了一个解的邻域,就像图1中血缘关系定义了你的家人集合一样。可能大家对生活中的例子都有一个比较感性的认识,但对于启发式中的就觉得比较抽象。
下面我再举一个简单的例子:
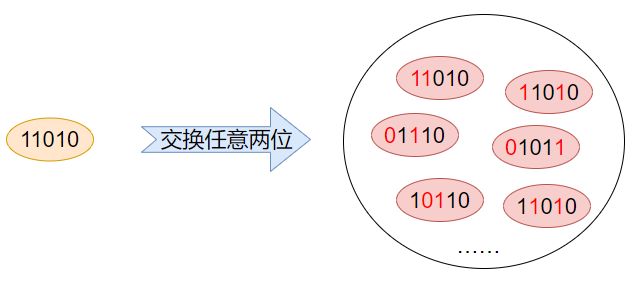
对于一个背包问题的解s_bp = 11010,它的各个位上对应的值如下:
| 位 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 值 | 1 | 1 | 0 | 1 | 0 |
现在定义一个邻域结构:**交换任意两位。**那么解s_bp能够形成的邻居解就有 C 5 2 = 10 C_5^2=10 C52=10个。比如交换第1、第二位上的两个1,得到11010;交换第1、第3位上的1和0,得到01110……等等。最终邻域生成如下图所示:
邻域结构的设计在启发式算法中非常重要,它直接决定了搜索的范围,对最终的搜索结构有着重要的影响。其实,按照小编的经验来讲,邻域结构的设计直接决定了最终结果质量的好坏。当然这只是我的一些个人经验,毕竟启发式算法这东西不像精确式算法那样具有很强的理论性,它更多注重的是应用,而应用就和经验挂钩了。所以一千个读者有一千个哈姆雷特也不足为奇。
搜索过程
此前我们说过,邻域搜索本质还是一个局部搜索的过程,事实上,它就是通过邻域搜索进行局部探优的,并且往往是多个“局部区域”进行搜索的,那么它是怎么确定搜索区域,又是怎么搜索的呢?下面我们一步一步给大家演示,看完相信大家就豁然开朗啦。
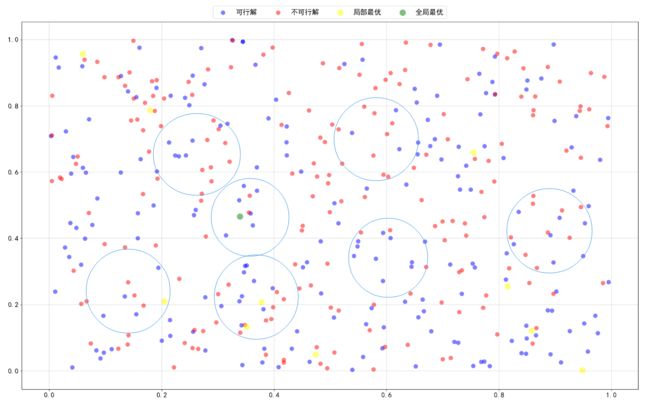
假如初始时我们有以下的解空间,其中绿色的是最优解,如下(密恐福利):
STEP1:初始解生成
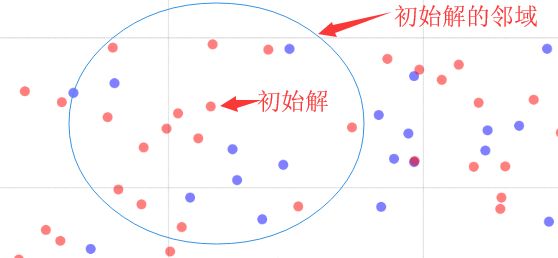
因为邻域是基于一个解生成的,要想进行邻域搜索,得先有一个解。所以首先要做的,当然是生成初始解啦。一般初始解都采用构造法进行生成,比如随机构造啦,之前讲的贪心构造啦等,怎样,是不是明白什么了呢。假如我们现在构造了一个初始解如下(它位于图上方偏右):
STEP2:邻域生成
有了初始解,接下来就可以根据所定义的邻域结构生成邻域了:
STEP3:评价
现在邻域有了,即要搜索的局部已经确定下来,我们是不是得进去找想要的东西了呀!评价就是在解的邻域范围内对邻居解进行评价,然后选出需要的邻居解进行“移动”。一般而言,有两种评价的模式:
- first improve:首次提升原则,即在邻域内对解一一进行评价,一旦发现比当前解更优的邻居解立马进行“移动”。
- best improve:最优提升原则,遍历整个邻域,找出最好的邻居解进行“移动”。
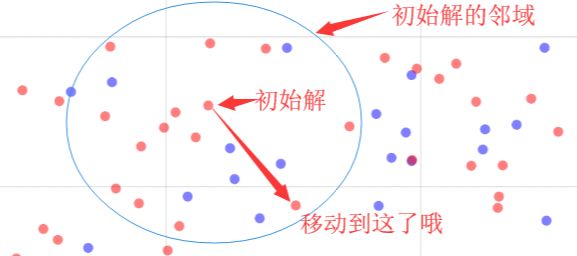
STEP4:移动
何为移动呢?其实就是当前解变换到刚刚评价选择的邻居解的过程。初始解在其邻域内找到了一个更好的邻居解,然后移动过去了,如下图所示:
STEP5:记录全局最优解
如果当前解比全局最优解还要优,那么更新全局最优解。
然后接下来的过程大家应该都知道了,就是不断重复STEP2-STEP5,直到满足终止条件,最后输出全局最优解。如果算法足够优秀加上运气buff的话,最后找到全局最优是没有问题的:
糟糕!陷入局部最优了
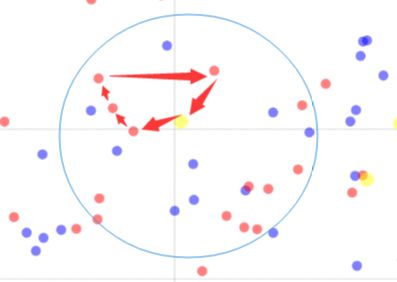
这里有必要再讲讲上述搜索过程中:STEP3:评价这一步骤。当我们以first improve或者best improve对当前解的邻居进行评价时,通常的做法是找到比当前解要好的邻居解进行移动。但往往出现的情况是当前解的邻域中并不存在更优的邻居解,如下图:
初始解即生成在了一个局部最优上面,这时候我们通常选择邻域中一个最好的邻居解进行移动(尽管它比当前解还要差),如果不这样做那就彻底陷入局部最优了。
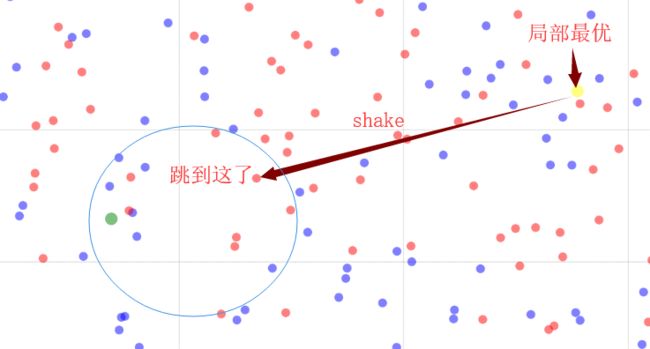
但是这样做还有可能发生一个问题,它在兜兜转转移来移去结果又给移回去了:
这种情况也可以认为是陷入了局部最优,通常的判断条件就是经过多次邻域搜索依旧没有得到很好的improve。这种情况怎么办呢?当然是“跳一跳”啦,如下:
这种“跳一跳”在启发式中被称为shake或者perturbation,中文称之为扰动。是跳出局部最优一个非常有效的做法。通常的实现方式是利用随机或者其他方式,对当前解进行重组,使其结构发生较大的改变。或者直接抛弃当前解,重新生成一个解进行后续的邻域搜索。
随机因素
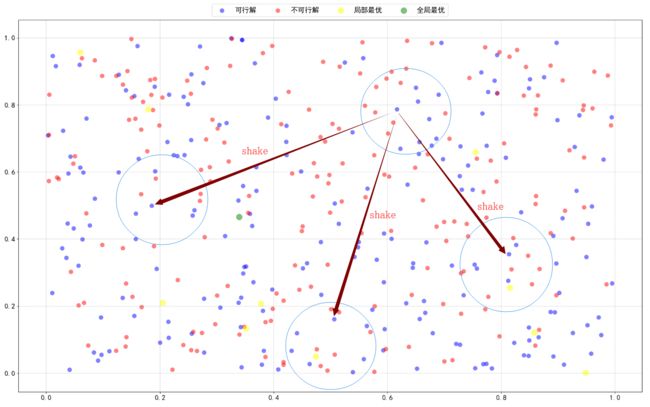
随机因素也是启发式算法的一大特色了,因为无法判断搜索“区域”的好坏,我们一般会随机进行选择搜索,比如初始解的生成就有很多种可能性:
如果你长得足够好看的话,直接生成最优解也不是不可能。每一个初始解对应的邻域不同,搜索的路径就不同。但通常经过优化,各个初始解基本都能收敛到一个比较接近的水平。同时,shake也是一个随机过程:
这也是为什么很多新手朋友喜欢找到我,张口就来:小编你的代码有错!每次结果都不一样的。
小结
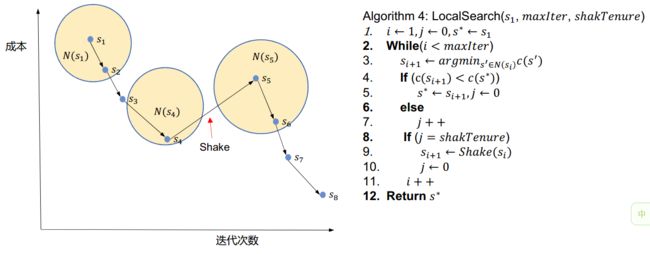
看了上述的过程,大家明白邻域搜索和局部搜索这种千丝万缕的关系了吧。最后放上一个基于邻域的局部搜索算法伪代码帮助大家更好理解:
符号:
- s i s_i si:第 i i i次迭代的解。
- N ( s i ) N(s_i) N(si):解 s i s_i si的邻域。
- m a x I t e r maxIter maxIter:最大迭代次数。
- s h a k e T e n n u r e shakeTennure shakeTennure:执行扰动的周期。
- S h a k e ( s ) Shake(s) Shake(s):对解 s s s进行扰动。
实验部分
上一篇文章中大家看到了贪心算法对于背包问题效果似乎很不错,也能在较短的时间内找出接近最优解的满意解。是不是就意味着我们可以抛弃其他算法,拥抱贪心了呢?
当然不是,0-1背包问题其实还是比较容易的,捏软柿子其实说明不了什么。所以我们这次测试的问题改成了TSP问题,算例来源TSPLIB网站。关于算例文件和最优解可以关注公众号【程序猿声】在资源下载一栏可以进行下载。
枚举法是什么体验?
对于TSP问题,如果用枚举的话,大家想想全枚举会有多少中组合呢?假如有N个城市,那么全枚举就是N个城市的全排列,总数就是N的阶乘N!。好了大家可能还是没有什么概念,假如N=20(很小的规模了),那么其阶乘的结果是2432902008176640000。用枚举?简直连想都不敢想。
贪心和启发式
对于Greedy,其思想是随机生成第一个城市,加入cityList,然后从剩下的依次找离cityList最后一个城市最近的放进去。参见最近邻域法–nearest neighborhood search。
protected int[] createGreedyRandomizedTour(int dimension) {
int[] newTour = new int[dimension];
Set<Integer> unvisitedCities = new HashSet<>();
for(int i = 1; i <= dimension; i++)
unvisitedCities.add(i);
newTour[0] = rnd.nextInt(dimension)+1;
unvisitedCities.remove(newTour[0]);
for(int i = 1; i < dimension; i++){
int nearestCity = getNearestCity(newTour[i-1], unvisitedCities);
newTour[i] = nearestCity;
unvisitedCities.remove(nearestCity);
}
return newTour;
}
protected int getNearestCity(int city, Set<Integer> endpoints) {
Iterator<Integer> it = endpoints.iterator();
int nearestCity = 0;
double minDistance = Double.MAX_VALUE;
while (it.hasNext()) {
int i = it.next();
// boolean containedInParents = (neighbours1[city - 1][0] == i
// || neighbours1[city - 1][1] == i
// || neighbours2[city - 1][0] == i || neighbours2[city - 1][1] == i);
if (distanceTable.getDistanceBetween(city, i) < minDistance
) {
minDistance = distanceTable.getDistanceBetween(city, i);
nearestCity = i;
}
}
if (nearestCity != 0)
return nearestCity;
else //treats the case that all possible edges are already contained in the parents
{
it = endpoints.iterator();
while (it.hasNext()) {
int i = it.next();
if (distanceTable.getDistanceBetween(city, i) < minDistance) {
minDistance = distanceTable.getDistanceBetween(city, i);
nearestCity = i;
}
}
return nearestCity;
}
}
对于Local Search,初始解是贪心生成的,只用了一种邻域结构,2-opt(i, j),其中 i , j ∈ C , i ≠ j i, j \in C, i \neq j i,j∈C,i=j。如果有改进那么会一直进行2-opt全邻域搜索,没有的话就在greedy一个解进行下一轮邻域搜索。1000次迭代。
public double[] executeAlgorithm(int iterationNr) {
System.out.println(getOptimalDistance());
long startTime = System.currentTimeMillis();
Tour t = Tour.createTour(createGreedyRandomizedTour(instance.getDimension()));
Tour bestFoundSolution = t;
double greedyCost = t.distance(instance);
long greedyTime = System.currentTimeMillis()- startTime;
int numberOfRestarts = 0;
startTime = System.currentTimeMillis();
while (numberOfRestarts <= iterationNr){
TSP2OptHeuristic heuristic = new TSP2OptHeuristic(instance);
heuristic.apply(t);
results.add(relativeDistance(t));
bestFoundSolution = bestFoundSolution.distance(instance) > t.distance(instance) ? t : bestFoundSolution;
numberOfRestarts++;
t = Tour.createTour(createGreedyRandomizedTour(instance.getDimension()));
}
long localSearchTime = System.currentTimeMillis()- startTime;
// System.out.println(System.currentTimeMillis()-startTime);
//System.out.println("Number of restarts: " + numberOfRestarts);
double bestFoundCost = bestFoundSolution.distance(instance);
return new double[]{greedyCost, bestFoundCost, getOptimalDistance(),relativeDistance(greedyCost),relativeDistance(bestFoundCost),
greedyTime, localSearchTime};
}
/**
* Applies the 2-opt heuristic to the specified tour.
*
* @param tour the tour that is modified by the 2-opt heuristic
*/
public void apply(Tour tour) {
DistanceTable distanceTable = instance.getDistanceTable();
boolean modified = true;
// tours with 3 or fewer nodes are already optimal
if (tour.size() < 4) {
return;
}
while (modified) {
modified = false;
for (int i = 0; i < tour.size(); i++) {
for (int j = i+2; j < tour.size(); j++) {
double d1 = distanceTable.getDistanceBetween(tour.get(i), tour.get(i+1)) +
distanceTable.getDistanceBetween(tour.get(j), tour.get(j+1));
double d2 = distanceTable.getDistanceBetween(tour.get(i), tour.get(j)) +
distanceTable.getDistanceBetween(tour.get(i+1), tour.get(j+1));
// if distance can be shortened, adjust the tour
if (d2 < d1) {
tour.reverse(i+1, j);
modified = true;
}
}
}
}
}
Summary
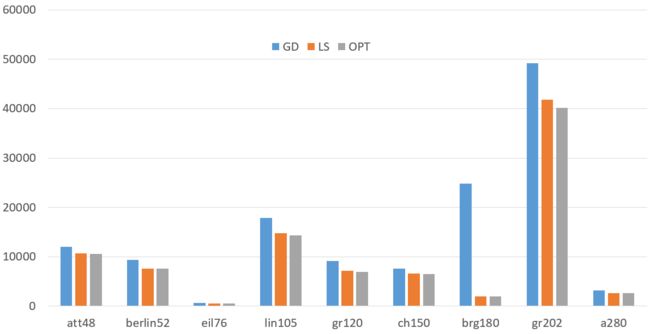
我们上述的Greedy和LocalSearch对9个TSP算例进行了测试,结果如下表所示:
| Inst | GD(1 runs) | LS(1 runs) | OPT | GD Gap(%) | LS Gap(%) | GD Time(1 runs) | LS Time(1 runs) |
|---|---|---|---|---|---|---|---|
| att48 | 12012 | 10725 | 10628 | 13.02 | 0.91 | 0.001 | 1.042 |
| berlin52 | 9323 | 7542 | 7542 | 23.61 | 0 | 0 | 0.685 |
| eil76 | 657 | 550 | 538 | 22.12 | 2.23 | 0 | 1.443 |
| lin105 | 17812 | 14732 | 14379 | 23.88 | 2.45 | 0.001 | 3.559 |
| gr120 | 9145 | 7131 | 6942 | 31.73 | 2.72 | 0.005 | 1.522 |
| ch150 | 7627 | 6646 | 6528 | 16.84 | 1.81 | 0.009 | 6.858 |
| brg180 | 24800 | 1960 | 1950 | 1171.79 | 0.51 | 0.001 | 2.081 |
| gr202 | 49181 | 41801 | 40160 | 22.46 | 4.09 | 0.026 | 276.969 |
| a280 | 3147 | 2675 | 2579 | 22.02 | 3.72 | 0.003 | 29.593 |
其中:
- Inst表示算例的名称。
- GD(1 runs)表示运行一次,Greedy得到的解的距离。
- LS(1 runs)表示运行一次,LocalSearch得到的解的距离。
- OPT表示该算例下的最优解。
- GD Gap(%)表示GD(1 runs)与OPT的差值(GD(1 runs) - OPT)/ OPT * 100,越小证明Greedy越好。
- LS Gap(%)表示LS(1 runs)与OPT的差值(LS(1 runs)- OPT)/ OPT * 100,越小证明LocalSearch越好。
- GD Time(1 runs)表示Greedy运行时间。
- LS Time(1 runs)表示LocalSearch运行时间。
下面我们从几个方面看看吧。
解的质量
可能直接看表不太直观,我们做成图看看:
可以明显看到,Greedy比LocalSearch还是差了不少的啊。每个算例均比LocalSearch高出不少,个别算例还高出一大截。究竟差了多少,我们可以从上表中的Gap列看出。Greedy比最优解普遍要高出10%-30%不等,有的甚至超过了1000%,而LocalSearch与最优解相差维持在5%以内。这时候就充分体现了LocalSearch的优势,Greedy的劣势了。
时间上的差异
emm……时间就不用对比了,Greedy秒天秒地秒空气,单凭速度上而言,构造法应该是最快的了。不过这里提一下LocalSearch的时间。看下面的图:
通常而言,启发式算法的运行时间和终止条件密切相关。比如迭代次数,运行时间限制,无改进终止等。与精确算法之类的不同,启发式算法抛开终止条件谈运行时间是没有意义的。因为对于精确算法、枚举算法、构造法,他们都有一个明确的目标:
- 精确算法、枚举算法:找到最优解后终止。
- 构造法:构造一个解之后终止。
而对于启发式而言,首先我不知道最优解,所以我也不能确定找到的解是不是最优解。所以,它的终止条件是认为设定的,这就意味着时间也是认为控制的。通常而言,时间越长找到的解质量越优,但所有的启发式找到的都是满意解,不能说是最优解(即便真的是),因为它遍历的是解空间的局部。
一般情况下,启发式算法的时间是随着问题规模增长而呈线性增长的。这也是它的最大优势之一,比如说你问题规模扩大一倍,那么我的算法在同样的终止条件下运行时间也基本上是翻倍、或者变成几倍而已,是一个平缓的线性增长。不会说变成 2 n 2^n 2n倍这种指数级别爆炸式的增长。从上面的时间曲线也可以看出,至于为什么在算例gr202上面顶了个小帐篷呢,是因为我们设置了一个比较坑爹的搜索条件,有改进就持续进行搜索。大家可以想一下:
红色路径的搜索过程时间肯定要比绿色路径的长。
总结
哈哈看到这里,想必大家也很不容易了。最后我想再问大家一个问题:启发式算法相比Greedy算法来说好像并没有提高多少(从上图可以看出),为什么呢?花数千倍甚至万倍的时间提高这么一点,有意义吗?
首先回答为什么。其实这个问题也很好回答,你打游戏的时候从1级升到20级是很容易的,但是从20级升到30级难度就不可同日而语了。对于优化也是一样,解的质量越高,就越难以提升。
至于有没有意义,对于现在的工业化社会而言,哪怕提升的只是一个小数点,放大到成千上万的生产量上面,降低的成本都是极大的。这也是为什么精确算法很难应用到企业中去,但依然有一大堆学者孜孜不倦最求研究的原因。
欲下载本文相关的完整代码及算例,请关注公众号【程序猿声】,后台回复【GDLSTSP】不包括【】即可
![]()