Assignment | 05-week1 -Building your Recurrent Neural Network - Step by Step
该系列仅在原课程基础上课后作业部分添加个人学习笔记,如有错误,还请批评指教。- ZJ
Coursera 课程 |deeplearning.ai |网易云课堂
CSDN:http://blog.csdn.net/JUNJUN_ZHAO/article/details/79400107
Welcome to Course 5’s first assignment! In this assignment, you will implement your first Recurrent Neural Network in numpy.
Recurrent Neural Networks (RNN) are very effective for Natural Language Processing and other sequence tasks because they have “memory”. They can read inputs x⟨t⟩ x ⟨ t ⟩ (such as words) one at a time, and remember some information/context through the hidden layer activations that get passed from one time-step to the next. This allows a uni-directional RNN to take information from the past to process later inputs. A bidirection RNN can take context from both the past and the future.
欢迎来到课程5的第一项任务! 在这个任务中,你将使用 numpy 实现你的第一个循环神经网络。
循环神经网络(RNN)对自然语言处理和其他序列任务非常有效,因为它们具有“记忆”细胞的作用。 他们可以一次读取一个输入 x⟨t⟩ x ⟨ t ⟩ (例如单词),并通过从一个时间步到另一个时间步的隐藏层激活记住一些信息/上下文。 这允许单向 RNN 从过去获取信息以处理稍后的输入。 双向 RNN 可以从过去和未来中获取背景信息。
Notation:
- Superscript [l] [ l ] denotes an object associated with the lth l t h layer. 层
- Example: a[4] a [ 4 ] is the 4th 4 t h layer activation. 第 4 层的激活值 W[5] W [ 5 ] and b[5] b [ 5 ] are the 5th 5 t h layer parameters. 第 5 层的参数
Superscript (i) ( i ) denotes an object associated with the ith i t h example. 样本
- Example: x(i) x ( i ) is the ith i t h training example input. 第 i 个输入 训练样本
Superscript ⟨t⟩ ⟨ t ⟩ denotes an object at the tth t t h time-step. 时间步
- Example: x⟨t⟩ x ⟨ t ⟩ is the input x at the tth t t h time-step. x(i)⟨t⟩ x ( i ) ⟨ t ⟩ is the input at the tth t t h time-step of example i i .
Lowerscript i i denotes the ith i t h entry of a vector. 一个向量的 第 i 个值
- Example: a[l]i a i [ l ] denotes the ith i t h entry of the activations in layer l l .
We assume that you are already familiar with numpy and/or have completed the previous courses of the specialization. Let’s get started!
【知乎】Softmax 函数的特点和作用是什么? https://www.zhihu.com/question/23765351
Let’s first import all the packages that you will need during this assignment.
import numpy as np
from rnn_utils import *'''
rnn_utils 中的代码
'''
import numpy as np
# https://www.zhihu.com/question/23765351 Softmax 函数的特点和作用是什么?
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0)
# softmax(x)
# 如 x = [1, 5, 3]
# x - np.max(x) 相当于 [1, 5, 3] - [5, 5, 5] = [-1, 0, -2] 避免值过大 所以都# 剪去最大值,按比例缩小
# 然后 np.exp(x - np.max(x)) 逐一计算,数组中每一个元素的 指数
# e_x / e_x.sum(axis=0) 得出最后结果
# b = np.array([2,3,4]) b.shape = (3,)
# c = np.mat([2,3,4]) c.shape = (1,3)
# d = np.mat([[1],[2],[3]]) d.shape = (3,1)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
# 由上面的Arguments 中的 对 parameters 描述可知,parameters 字典中包含所有参数,
# 参数有 w and b 两种,所以 //2 取小的整数 (7 //2 = 3 , -3 //2 = -2)
L = len(parameters) // 2 # number of layers in the neural networks 神经网络的层数
v = {}
s = {}
# Initialize v, s. Input: "parameters". Outputs: "v, s". 初始化 要输出的 "v, s"字典中要包含的参数 v["dW"] = 0 ,v["db"] = 0, s["dW"] = 0, s["db"] = 0
# 它们的 shape 与 W 和 b 相同
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
s["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
s["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
### END CODE HERE ###
return v, s
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates 0.9
beta2 -- Exponential decay hyperparameter for the second moment estimates 0.999
epsilon -- hyperparameter preventing division by zero in Adam updates 1e-8
Returns:
parameters -- python dictionary containing your updated parameters 字典包含你要更新的参数
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2 # number of layers in the neural networks
v_corrected = {} # Initializing first moment estimate, python dictionary
s_corrected = {} # Initializing second moment estimate, python dictionary
# Perform Adam update on all parameters 更新所有参数
for l in range(L):
# Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1 - beta1) * grads["dW" + str(l+1)]
v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1 - beta1) * grads["db" + str(l+1)]
### END CODE HERE ###
# Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
### START CODE HERE ### (approx. 2 lines)
v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1 - beta1**t)
v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1 - beta1**t)
### END CODE HERE ###
# Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
### START CODE HERE ### (approx. 2 lines)
s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1 - beta2) * (grads["dW" + str(l+1)] ** 2)
s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1 - beta2) * (grads["db" + str(l+1)] ** 2)
### END CODE HERE ###
# Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
### START CODE HERE ### (approx. 2 lines)
s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)] / (1 - beta2 ** t)
s_corrected["db" + str(l+1)] = s["db" + str(l+1)] / (1 - beta2 ** t)
### END CODE HERE ###
# Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
### START CODE HERE ### (approx. 2 lines)
# 对于 后面 np.sqrt 那有些疑问哈,我看论文中原本的算法,以及吴恩达老师讲解的算法 epsilon 应该是在 np.sqrt 之后再加上的
# parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)] / np.sqrt(s_corrected["dW" + str(l+1)] + epsilon)
# parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)] / np.sqrt(s_corrected["db" + str(l+1)] + epsilon)
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)]/(np.sqrt(s_corrected["dW" + str(l+1)])+epsilon)
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)]/(np.sqrt(s_corrected["db" + str(l+1)])+epsilon)
### END CODE HERE ###
return parameters, v, s1 - Forward propagation for the basic Recurrent Neural Network
Later this week, you will generate music using an RNN. The basic RNN that you will implement has the structure below. In this example, Tx=Ty T x = T y .
Here’s how you can implement an RNN:
Steps:
1. Implement the calculations needed for one time-step of the RNN.
2. Implement a loop over Tx T x time-steps in order to process all the inputs, one at a time.
Let’s go!
1.1 - RNN cell
A Recurrent neural network can be seen as the repetition 重复 of a single cell. You are first going to implement the computations for a single time-step. The following figure describes the operations for a single time-step of an RNN cell.
循环神经网络可以被看作是单个细胞的重复。 你首先要实现一个时间步骤的计算。 下图描述了 RNN 单元的单个时间步骤的操作。
Exercise: Implement the RNN-cell described in Figure (2).
Instructions:
1. Compute the hidden state with tanh activation: a⟨t⟩=tanh(Waaa⟨t−1⟩+Waxx⟨t⟩+ba) a ⟨ t ⟩ = tanh ( W a a a ⟨ t − 1 ⟩ + W a x x ⟨ t ⟩ + b a ) .
2. Using your new hidden state a⟨t⟩ a ⟨ t ⟩ , compute the prediction y^⟨t⟩=softmax(Wyaa⟨t⟩+by) y ^ ⟨ t ⟩ = s o f t m a x ( W y a a ⟨ t ⟩ + b y ) . We provided you a function: softmax.
3. Store (a⟨t⟩,a⟨t−1⟩,x⟨t⟩,parameters) ( a ⟨ t ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ , p a r a m e t e r s ) in cache
4. Return a⟨t⟩ a ⟨ t ⟩ , y⟨t⟩ y ⟨ t ⟩ and cache
We will vectorize over m m examples. Thus, x⟨t⟩ x ⟨ t ⟩ will have dimension (nx,m) ( n x , m ) , and a⟨t⟩ a ⟨ t ⟩ will have dimension (na,m) ( n a , m ) .
# GRADED FUNCTION: rnn_cell_forward
def rnn_cell_forward(xt, a_prev, parameters):
"""
Implements a single forward step of the RNN-cell as described in Figure (2)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
"""
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ### (≈2 lines)
# compute next activation state using the formula given above np.tanh
a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
# compute output of the current cell using the formula given above 注意使用上面计算出来的 a_next 值,进行下一步计算 softmax 在rnn_utils 中
yt_pred = softmax(np.dot(Wya, a_next) + by)
### END CODE HERE ###
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cachenp.random.seed(1)
# randn 标准正太分布中 返回值
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)a_next[4] = [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978
-0.18887155 0.99815551 0.6531151 0.82872037]
a_next.shape = (5, 10)
yt_pred[1] = [0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
0.36920224 0.9966312 0.9982559 0.17746526]
yt_pred.shape = (2, 10)
Expected Output:
| **a_next[4]**: | [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978 -0.18887155 0.99815551 0.6531151 0.82872037] |
| **a_next.shape**: | (5, 10) |
| **yt[1]**: | [ 0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212 0.36920224 0.9966312 0.9982559 0.17746526] |
| **yt.shape**: | (2, 10) |
1.2 - RNN forward pass
You can see an RNN as the repetition of the cell you’ve just built. If your input sequence of data is carried over 10 time steps, then you will copy the RNN cell 10 times. Each cell takes as input the hidden state from the previous cell ( a⟨t−1⟩ a ⟨ t − 1 ⟩ ) and the current time-step’s input data ( x⟨t⟩ x ⟨ t ⟩ ). It outputs a hidden state ( a⟨t⟩ a ⟨ t ⟩ ) and a prediction ( y⟨t⟩ y ⟨ t ⟩ ) for this time-step.
Exercise: Code the forward propagation of the RNN described in Figure (3).
Instructions:
1. Create a vector of zeros ( a a ) that will store all the hidden states computed by the RNN.
2. Initialize the “next” hidden state as a0 a 0 (initial hidden state).
3. Start looping over each time step, your incremental index is t t :
- Update the “next” hidden state and the cache by running rnn_cell_forward
- Store the “next” hidden state in a a ( tth t t h position)
- Store the prediction in y
- Add the cache to the list of caches
4. Return a a , y y and caches
1.创建一个零向量( a a ),它将存储由 RNN 计算的所有隐藏状态。
2.将“下一个”隐藏状态初始化为 a0 a 0 (初始隐藏状态)。
3.开始循环遍历每个时间步,您的增量索引是 t t :
- 通过运行rnn_cell_forward来更新“下一个”隐藏状态和缓存
- 将“下一个”隐藏状态存储在 a a ( tth t t h 位置)
- 将预测存储在 y 中
- 将缓存添加到缓存列表
4.返回 a a , y y 并缓存
# GRADED FUNCTION: rnn_forward
def rnn_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network described in Figure (3).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of caches, x)
"""
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and Wya
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
### START CODE HERE ###
# initialize "a" and "y" with zeros (≈2 lines)
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# Initialize a_next (≈1 line)
a_next = a0
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈1 line)
a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y_pred[:,:,t] = yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
# 错误点: x.shape 大小这么表示np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])
print("len(caches) = ", len(caches))a[4][1] = [-0.99999375 0.77911235 -0.99861469 -0.99833267]
a.shape = (5, 10, 4)
y_pred[1][3] = [0.79560373 0.86224861 0.11118257 0.81515947]
y_pred.shape = (2, 10, 4)
caches[1][1][3] = [-1.1425182 -0.34934272 -0.20889423 0.58662319]
len(caches) = 2
Expected Output:
| **a[4][1]**: | [-0.99999375 0.77911235 -0.99861469 -0.99833267] |
| **a.shape**: | (5, 10, 4) |
| **y[1][3]**: | [ 0.79560373 0.86224861 0.11118257 0.81515947] |
| **y.shape**: | (2, 10, 4) |
| **cache[1][1][3]**: | [-1.1425182 -0.34934272 -0.20889423 0.58662319] |
| **len(cache)**: | 2 |
Congratulations! You’ve successfully built the forward propagation of a recurrent neural network from scratch. This will work well enough for some applications, but it suffers from vanishing gradient problems. So it works best when each output y⟨t⟩ y ⟨ t ⟩ can be estimated using mainly “local” context (meaning information from inputs x⟨t′⟩ x ⟨ t ′ ⟩ where t′ t ′ is not too far from t t ).
In the next part, you will build a more complex LSTM model, which is better at addressing vanishing gradients. The LSTM will be better able to remember a piece of information and keep it saved for many timesteps.
恭喜! 您已经成功构建了从头开始的循环神经网络的向前传播。 这对于某些应用程序来说可以工作得很好,但是会遇到逐渐消失的梯度问题。 因此,当每个输出 y⟨t⟩ y ⟨ t ⟩ 可以使用主要的“local”上下文(意思是来自输入信息 x⟨t′⟩ x ⟨ t ′ ⟩ ,其中 t′ t ′ 是 离 t t 不太远)。
在接下来的部分中,您将构建一个更复杂的 LSTM 模型,该模型更适合处理消失渐变。 LSTM 将能够更好地记住一段信息,并将其保存多个时间步。
2 - Long Short-Term Memory (LSTM) network 长短时记忆网络
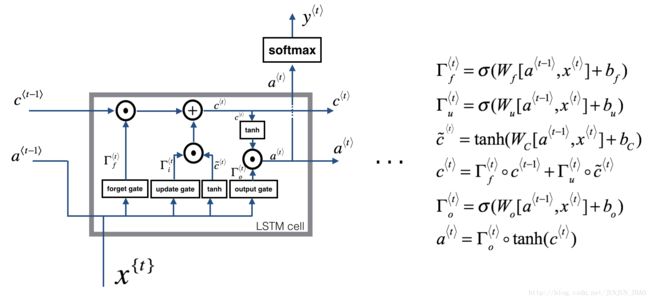
This following figure shows the operations of an LSTM-cell.
Similar to the RNN example above, you will start by implementing the LSTM cell for a single time-step. Then you can iteratively call it from inside a for-loop to have it process an input with Tx T x time-steps.
与上面的 RNN 例子相似,首先先实现一个时间步的 LSTM 单元,然后再迭代循环调用。
About the gates
- Forget gate
For the sake of this illustration, lets assume we are reading words in a piece of text, and want use an LSTM to keep track of grammatical structures 语法结构, such as whether the subject 主语 is singular or plural单数还是复数. If the subject changes from a singular word to a plural word, we need to find a way to get rid of our previously stored memory value of the singular/plural state. In an LSTM, the forget gate lets us do this: 如果主语从单数变为复数,那么需要去掉之前存储的记忆值, LSTM 中的遗忘门 就是做这件事的。
Here, Wf W f are weights that govern the forget gate’s behavior. We concatenate 连接 [a⟨t−1⟩,x⟨t⟩] [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] and multiply by Wf W f . The equation above results in a vector Γ⟨t⟩f Γ f ⟨ t ⟩ with values between 0 and 1. This forget gate vector will be multiplied element-wise by the previous cell state c⟨t−1⟩ c ⟨ t − 1 ⟩ . So if one of the values of Γ⟨t⟩f Γ f ⟨ t ⟩ is 0 (or close to 0) then it means that the LSTM should remove that piece of information (e.g. the singular subject) in the corresponding component of c⟨t−1⟩ c ⟨ t − 1 ⟩ . If one of the values is 1, then it will keep the information. 若遗忘门的值是 0 或接近 0 那么 移除掉 c⟨t−1⟩ c ⟨ t − 1 ⟩ 的信息
- Update gate
Once we forget that the subject being discussed is singular, we need to find a way to update it to reflect that the new subject is now plural. Here is the formulat for the update gate: 找到一个方法去更新它,现在的主语是复数
Similar to the forget gate, here Γ⟨t⟩u Γ u ⟨ t ⟩ is again a vector of values between 0 and 1. This will be multiplied element-wise with c~⟨t⟩ c ~ ⟨ t ⟩ , in order to compute c⟨t⟩ c ⟨ t ⟩ .
- Updating the cell
To update the new subject we need to create a new vector of numbers that we can add to our previous cell state. The equation we use is:
Finally, the new cell state is:
- Output gate
To decide which outputs we will use, we will use the following two formulas:
Where in equation 5 you decide what to output using a sigmoid function and in equation 6 you multiply that by the tanh tanh of the previous state.
2.1 - LSTM cell
Exercise: Implement the LSTM cell described in the Figure (3).
Instructions:
1. Concatenate a⟨t−1⟩ a ⟨ t − 1 ⟩ and x⟨t⟩ x ⟨ t ⟩ in a single matrix: concat=[a⟨t−1⟩x⟨t⟩] c o n c a t = [ a ⟨ t − 1 ⟩ x ⟨ t ⟩ ]
2. Compute all the formulas 1-6. You can use sigmoid() (provided) and np.tanh().
3. Compute the prediction y⟨t⟩ y ⟨ t ⟩ . You can use softmax() (provided).
# GRADED FUNCTION: lstm_cell_forward
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
"""
Implement a single forward step of the LSTM-cell as described in Figure (4)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
c_next -- next memory state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)
Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),
c stands for the memory value
"""
# Retrieve parameters from "parameters"
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
### START CODE HERE ###
# Concatenate a_prev and xt (≈3 lines) 连接矩阵时,先计算好,矩阵的形状大小,初始化 zeros 然后再对应部分再 添加对应矩阵
concat = np.zeros((n_x + n_a, m))
concat[: n_a, :] = a_prev
concat[n_a :, :] = xt
# Compute values for ft, it, cct, c_next, ot, a_next using the formulas given figure (4) (≈6 lines)
ft = sigmoid(np.matmul(Wf, concat) + bf)
it = sigmoid(np.matmul(Wi, concat) + bi)
cct = np.tanh(np.matmul(Wc, concat) + bc)
c_next = it * cct + ft * c_prev
ot = sigmoid(np.matmul(Wo, concat) + bo)
a_next = ot * np.tanh(c_next)
# Compute prediction of the LSTM cell (≈1 line)
yt_pred = softmax(np.matmul(Wy,a_next) + by)
### END CODE HERE ###
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cachenp.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
print("cache[1][3] =", cache[1][3])
print("len(cache) = ", len(cache))a_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape = (5, 10)
c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape = (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape = (2, 10)
cache[1][3] = [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874
0.07651101 -1.03752894 1.41219977 -0.37647422]
len(cache) = 10
Expected Output:
| **a_next[4]**: | [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482 0.76566531 0.34631421 -0.00215674 0.43827275] |
| **a_next.shape**: | (5, 10) |
| **c_next[2]**: | [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942 0.76449811 -0.0981561 -0.74348425 -0.26810932] |
| **c_next.shape**: | (5, 10) |
| **yt[1]**: | [ 0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381 0.00943007 0.12666353 0.39380172 0.07828381] |
| **yt.shape**: | (2, 10) |
| **cache[1][3]**: | [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874 0.07651101 -1.03752894 1.41219977 -0.37647422] |
| **len(cache)**: | 10 |
2.2 - Forward pass for LSTM
Now that you have implemented one step of an LSTM, you can now iterate this over this using a for-loop to process a sequence of Tx T x inputs.
Exercise: Implement lstm_forward() to run an LSTM over Tx T x time-steps.
Note: c⟨0⟩ c ⟨ 0 ⟩ is initialized with zeros.
# GRADED FUNCTION: lstm_forward
def lstm_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (3).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)
"""
# Initialize "caches", which will track the list of all the caches
caches = []
### START CODE HERE ###
# Retrieve dimensions from shapes of x and Wy (≈2 lines)
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wy"].shape
# initialize "a", "c" and "y" with zeros (≈3 lines)
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
# Initialize a_next and c_next (≈2 lines)
a_next = a0
c_next = np.zeros(a_next.shape)
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
a_next, c_next, yt, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t] = yt
# Save the value of the next cell state (≈1 line)
c[:,:,t] = c_next
# Append the cache into caches (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, cachesnp.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a, y, c, caches = lstm_forward(x, a0, parameters)
print("a[4][3][6] = ", a[4][3][6])
print("a.shape = ", a.shape)
print("y[1][4][3] =", y[1][4][3])
print("y.shape = ", y.shape)
print("caches[1][1[1]] =", caches[1][1][1])
print("c[1][2][1]", c[1][2][1])
print("len(caches) = ", len(caches))a[4][3][6] = 0.17211776753291672
a.shape = (5, 10, 7)
y[1][4][3] = 0.9508734618501101
y.shape = (2, 10, 7)
caches[1][1[1]] = [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.8555449167181981
len(caches) = 2
Expected Output:
| **a[4][3][6]** = | 0.172117767533 |
| **a.shape** = | (5, 10, 7) |
| **y[1][4][3]** = | 0.95087346185 |
| **y.shape** = | (2, 10, 7) |
| **caches[1][1][1]** = | [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139 0.41005165] |
| **c[1][2][1]** = | -0.855544916718 |
| **len(caches)** = | 2 |
Congratulations! You have now implemented the forward passes for the basic RNN and the LSTM. When using a deep learning framework, implementing the forward pass is sufficient to build systems that achieve great performance.
The rest of this notebook is optional, and will not be graded.
3 - Backpropagation in recurrent neural networks (OPTIONAL / UNGRADED)
In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers do not need to bother with the details of the backward pass. If however you are an expert in calculus and want to see the details of backprop in RNNs, you can work through this optional portion of the notebook.
When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in recurrent neural networks you can to calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are quite complicated and we did not derive them in lecture. However, we will briefly present them below. 求导过程,这里不会进行详细推导,只是简单的展示结果。
在现代的深度学习框架中,您只需要实现前向传播,并且框架负责关注反向传播,因此大多数深度学习工程师不需要为反向传播的细节而烦恼。 但是,如果您是微积分专家,并希望查看 RNN 中 backprop 的详细信息,则可以通过笔记的这一可选部分进行操作。
在之前的课程中,您实现了一个简单的(完全连接的)神经网络,您使用反向传播来计算更新参数的费用方面的导数。 同样,在循环神经网络中,您可以根据成本计算导数以更新参数。 backprop方程相当复杂,我们在讲座中没有推导出它们。 但是,我们将在下面简要介绍它们。
3.1 - Basic RNN backward pass
We will start by computing the backward pass for the basic RNN-cell.
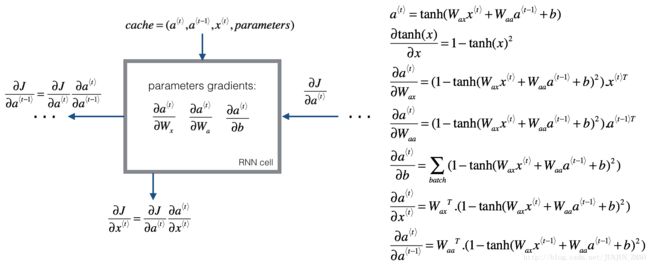
Deriving the one step backward functions:
To compute the rnn_cell_backward you need to compute the following equations. It is a good exercise to derive them by hand.
The derivative of tanh tanh is 1−tanh(x)2 1 − tanh ( x ) 2 . You can find the complete proof here. Note that: sec(x)2=1−tanh(x)2 sec ( x ) 2 = 1 − tanh ( x ) 2
Similarly for ∂a⟨t⟩∂Wax,∂a⟨t⟩∂Waa,∂a⟨t⟩∂b ∂ a ⟨ t ⟩ ∂ W a x , ∂ a ⟨ t ⟩ ∂ W a a , ∂ a ⟨ t ⟩ ∂ b , the derivative of tanh(u) tanh ( u ) is (1−tanh(u)2)du ( 1 − tanh ( u ) 2 ) d u .
The final two equations also follow same rule and are derived using the tanh tanh derivative. Note that the arrangement is done in a way to get the same dimensions to match.
def rnn_cell_backward(da_next, cache):
"""
Implements the backward pass for the RNN-cell (single time-step). 注意这里是 基本的 RNN 单元 网络的反向传播
Arguments:
da_next -- Gradient of loss with respect to next hidden state
cache -- python dictionary containing useful values (output of rnn_cell_forward())
Returns:
gradients -- python dictionary containing:
dxt -- Gradients of input data, of shape (n_x, m)
da_prev -- Gradients of previous hidden state, of shape (n_a, m)
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dba -- Gradients of bias vector, of shape (n_a, 1)
"""
# Retrieve values from cache
(a_next, a_prev, xt, parameters) = cache
# Retrieve values from parameters 先把之前存的参数提取出来
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ###
# compute the gradient of tanh with respect to a_next (≈1 line)
# 根据 提供的参数 da_next -- Gradient of loss with respect to next hidden state
# 以及 上面提到的公式 tanh(u) = (1- tanh(u)**2)*du ,这里的 du 就是 da_next tanh(u) 是 a_next
dtanh = (1 - a_next **2)* da_next
# compute the gradient of the loss with respect to Wax (≈2 lines)
dxt = np.dot(Wax.T, dtanh)
dWax = np.dot(dtanh, xt.T)
# compute the gradient with respect to Waa (≈2 lines)
da_prev = np.dot(Waa.T, dtanh)
dWaa = np.dot(dtanh, a_prev.T)
# compute the gradient with respect to b (≈1 line)
# axis=0 列方向上操作 axis=1 行方向上操作 keepdims=True 矩阵的二维特性
dba = np.sum(dtanh, axis=1, keepdims=True)
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dxt":dxt, "da_prev":da_prev,"dWax":dWax, "dWaa":dWaa, "dba":dba }
return gradientsnp.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
b = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)
da_next = np.random.randn(5,10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)gradients["dxt"][1][2] = -0.4605641030588796
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = 0.08429686538067671
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.3930818739219304
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = -0.2848395578696066
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [0.80517166]
gradients["dba"].shape = (5, 1)
Expected Output:
| **gradients[“dxt”][1][2]** = | -0.460564103059 |
| **gradients[“dxt”].shape** = | (3, 10) |
| **gradients[“da_prev”][2][3]** = | 0.0842968653807 |
| **gradients[“da_prev”].shape** = | (5, 10) |
| **gradients[“dWax”][3][1]** = | 0.393081873922 |
| **gradients[“dWax”].shape** = | (5, 3) |
| **gradients[“dWaa”][1][2]** = | -0.28483955787 |
| **gradients[“dWaa”].shape** = | (5, 5) |
| **gradients[“dba”][4]** = | [ 0.80517166] |
| **gradients[“dba”].shape** = | (5, 1) |
Backward pass through the RNN
Computing the gradients of the cost with respect to a⟨t⟩ a ⟨ t ⟩ at every time-step t t is useful because it is what helps the gradient backpropagate to the previous RNN-cell. To do so, you need to iterate through all the time steps starting at the end, and at each step, you increment the overall dba d b a , dWaa d W a a , dWax d W a x and you store dx d x .
Instructions:
Implement the rnn_backward function. Initialize the return variables with zeros first and then loop through all the time steps while calling the rnn_cell_backward at each time timestep, update the other variables accordingly.
def rnn_backward(da, caches):
"""
Implement the backward pass for a RNN over an entire sequence of input data.
Arguments:
da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x)
caches -- tuple containing information from the forward pass (rnn_forward)
Returns:
gradients -- python dictionary containing:
dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x)
da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m)
dWax -- Gradient w.r.t the input's weight matrix, numpy-array of shape (n_a, n_x)
dWaa -- Gradient w.r.t the hidden state's weight matrix, numpy-arrayof shape (n_a, n_a)
dba -- Gradient w.r.t the bias, of shape (n_a, 1)
"""
### START CODE HERE ###
# Retrieve values from the first cache (t=1) of caches (≈2 lines)
(caches, x) = caches
(a1, a0, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈6 lines)
dx = np.zeros((n_x, m, T_x))
dWax = np.zeros(parameters["Wax"].shape)
dWaa = np.zeros(parameters["Waa"].shape)
dba = np.zeros(parameters["ba"].shape)
da0 = np.zeros(a0.shape)
da_prevt = np.zeros((n_a, m))
# Loop through all the time steps
for t in reversed(range(T_x)):
# Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t])
# Retrieve derivatives from gradients (≈ 1 line)
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
# Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line)
da0 = da_prevt
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients
错误记录:
gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t])
第一个参数是: da[:,:,t] + da_prevt, 这里是每一次训练后的更新迭代
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)gradients["dx"][1][2] = [-2.07101689 -0.59255627 0.02466855 0.01483317]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.3149423751266499
gradients["da0"].shape = (5, 10)
gradients["dWax"][3][1] = 11.264104496527777
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 2.3033331265798926
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [-0.74747722]
gradients["dba"].shape = (5, 1)
Expected Output:
| **gradients[“dx”][1][2]** = | [-2.07101689 -0.59255627 0.02466855 0.01483317] |
| **gradients[“dx”].shape** = | (3, 10, 4) |
| **gradients[“da0”][2][3]** = | -0.314942375127 |
| **gradients[“da0”].shape** = | (5, 10) |
| **gradients[“dWax”][3][1]** = | 11.2641044965 |
| **gradients[“dWax”].shape** = | (5, 3) |
| **gradients[“dWaa”][1][2]** = | 2.30333312658 |
| **gradients[“dWaa”].shape** = | (5, 5) |
| **gradients[“dba”][4]** = | [-0.74747722] |
| **gradients[“dba”].shape** = | (5, 1) |
3.2 - LSTM backward pass
3.2.1 One Step backward
The LSTM backward pass is slighltly more complicated than the forward one. We have provided you with all the equations for the LSTM backward pass below. (If you enjoy calculus exercises feel free to try deriving these from scratch yourself.)
3.2.2 gate derivatives
3.2.3 parameter derivatives
To calculate dbf,dbu,dbc,dbo d b f , d b u , d b c , d b o you just need to sum across the horizontal (axis= 1) axis on dΓ⟨t⟩f,dΓ⟨t⟩u,dc~⟨t⟩,dΓ⟨t⟩o d Γ f ⟨ t ⟩ , d Γ u ⟨ t ⟩ , d c ~ ⟨ t ⟩ , d Γ o ⟨ t ⟩ respectively. Note that you should have the keep_dims = True option.
Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.
Here, the weights for equations 13 are the first n_a, (i.e. Wf=Wf[:na,:] W f = W f [ : n a , : ] etc…)
where the weights for equation 15 are from n_a to the end, (i.e. Wf=Wf[na:,:] W f = W f [ n a : , : ] etc…)
Exercise: Implement lstm_cell_backward by implementing equations 7−17 7 − 17 below. Good luck! :)
def lstm_cell_backward(da_next, dc_next, cache):
"""
Implement the backward pass for the LSTM-cell (single time-step).
Arguments:
da_next -- Gradients of next hidden state, of shape (n_a, m)
dc_next -- Gradients of next cell state, of shape (n_a, m)
cache -- cache storing information from the forward pass
Returns:
gradients -- python dictionary containing:
dxt -- Gradient of input data at time-step t, of shape (n_x, m)
da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x)
dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
dWo -- Gradient w.r.t. the weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
dbo -- Gradient w.r.t. biases of the output gate, of shape (n_a, 1)
"""
# Retrieve information from "cache"
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
### START CODE HERE ###
# Retrieve dimensions from xt's and a_next's shape (≈2 lines)
n_x, m = xt.shape
n_a, m = a_next.shape
# Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
dot = da_next * np.tanh(c_next) * ot * (1 - ot)
dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
dft = (dc_next * c_prev + ot *(1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)
# Code equations (7) to (10) (≈4 lines)
##dit = None
##dft = None
##dot = None
##dcct = None
concat = np.concatenate((a_prev, xt), axis=0)
# Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
dWf = np.dot(dft, concat.T)
dWi = np.dot(dit, concat.T)
dWc = np.dot(dcct, concat.T)
dWo = np.dot(dot, concat.T)
dbf = np.sum(dft, axis=1 ,keepdims = True)
dbi = np.sum(dit, axis=1, keepdims = True)
dbc = np.sum(dcct, axis=1, keepdims = True)
dbo = np.sum(dot, axis=1, keepdims = True)
# Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
da_prev = np.dot(parameters['Wf'][:, :n_a].T, dft) + np.dot(parameters['Wi'][:, :n_a].T, dit) + np.dot(parameters['Wc'][:, :n_a].T, dcct) + np.dot(parameters['Wo'][:, :n_a].T, dot)
dc_prev = dc_next * ft + ot * (1 - np.square(np.tanh(c_next))) * ft * da_next
dxt = np.dot(parameters['Wf'][:, n_a:].T, dft) + np.dot(parameters['Wi'][:, n_a:].T, dit) + np.dot(parameters['Wc'][:, n_a:].T, dcct) + np.dot(parameters['Wo'][:, n_a:].T, dot)
### END CODE HERE ###
# Save gradients in dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients错误记录:
parameters['Wf'][:, :n_a].T 每一行的 第 0 到 n_a-1 列的数据取出来
parameters['Wf'][:, n_a:].T 每一行的 第 n_a 到最后列的数据 取出来
dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
da_next = np.random.randn(5,10)
dc_next = np.random.randn(5,10)
gradients = lstm_cell_backward(da_next, dc_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)gradients["dxt"][1][2] = 3.230559115109188
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.06396214197109241
gradients["da_prev"].shape = (5, 10)
gradients["dc_prev"][2][3] = 0.7975220387970015
gradients["dc_prev"].shape = (5, 10)
gradients["dWf"][3][1] = -0.14795483816449725
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 1.0574980552259903
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 2.3045621636876668
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.3313115952892108
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [0.18864637]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.40142491]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [0.25587763]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [0.13893342]
gradients["dbo"].shape = (5, 1)
Expected Output:
| **gradients[“dxt”][1][2]** = | 3.23055911511 |
| **gradients[“dxt”].shape** = | (3, 10) |
| **gradients[“da_prev”][2][3]** = | -0.0639621419711 |
| **gradients[“da_prev”].shape** = | (5, 10) |
| **gradients[“dc_prev”][2][3]** = | 0.797522038797 |
| **gradients[“dc_prev”].shape** = | (5, 10) |
| **gradients[“dWf”][3][1]** = | -0.147954838164 |
| **gradients[“dWf”].shape** = | (5, 8) |
| **gradients[“dWi”][1][2]** = | 1.05749805523 |
| **gradients[“dWi”].shape** = | (5, 8) |
| **gradients[“dWc”][3][1]** = | 2.30456216369 |
| **gradients[“dWc”].shape** = | (5, 8) |
| **gradients[“dWo”][1][2]** = | 0.331311595289 |
| **gradients[“dWo”].shape** = | (5, 8) |
| **gradients[“dbf”][4]** = | [ 0.18864637] |
| **gradients[“dbf”].shape** = | (5, 1) |
| **gradients[“dbi”][4]** = | [-0.40142491] |
| **gradients[“dbi”].shape** = | (5, 1) |
| **gradients[“dbc”][4]** = | [ 0.25587763] |
| **gradients[“dbc”].shape** = | (5, 1) |
| **gradients[“dbo”][4]** = | [ 0.13893342] |
| **gradients[“dbo”].shape** = | (5, 1) |
3.3 Backward pass through the LSTM RNN
This part is very similar to the rnn_backward function you implemented above. You will first create variables of the same dimension as your return variables. You will then iterate over all the time steps starting from the end and call the one step function you implemented for LSTM at each iteration. You will then update the parameters by summing them individually. Finally return a dictionary with the new gradients.
Instructions: Implement the lstm_backward function. Create a for loop starting from Tx T x and going backward. For each step call lstm_cell_backward and update the your old gradients by adding the new gradients to them. Note that dxt is not updated but is stored.
def lstm_backward(da, caches):
"""
Implement the backward pass for the RNN with LSTM-cell (over a whole sequence).
Arguments:
da -- Gradients w.r.t the hidden states, numpy-array of shape (n_a, m, T_x)
dc -- Gradients w.r.t the memory states, numpy-array of shape (n_a, m, T_x)
caches -- cache storing information from the forward pass (lstm_forward)
Returns:
gradients -- python dictionary containing:
dx -- Gradient of inputs, of shape (n_x, m, T_x)
da0 -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x)
dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1)
"""
# Retrieve values from the first cache (t=1) of caches.
(caches, x) = caches
(a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
### START CODE HERE ###
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈12 lines)
dx = np.zeros((n_x, m, T_x))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
dc_prevt = np.zeros((n_a, m))
dWf = np.zeros((n_a, n_a + n_x))
dWi = np.zeros((n_a, n_a + n_x))
dWc = np.zeros((n_a, n_a + n_x))
dWo = np.zeros((n_a, n_a + n_x))
dbf = np.zeros((n_a, 1))
dbi = np.zeros((n_a, 1))
dbc = np.zeros((n_a, 1))
dbo = np.zeros((n_a, 1))
# loop back over the whole sequence
for t in reversed(range(T_x)):
# Compute all gradients using lstm_cell_backward
gradients = lstm_cell_backward(da[:, :, t], dc_prevt, caches[t])
# Store or add the gradient to the parameters' previous step's gradient
dx[:,:,t] = gradients["dxt"]
dWf = gradients["dWf"]
dWi = gradients["dWi"]
dWc = gradients["dWc"]
dWo = gradients["dWo"]
dbf = gradients["dbf"]
dbi = gradients["dbi"]
dbc = gradients["dbc"]
dbo = gradients["dbo"]
# Set the first activation's gradient to the backpropagated gradient da_prev.
da0 = gradients["da_prev"]
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradientsnp.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a, y, c, caches = lstm_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = lstm_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)gradients["dx"][1][2] = [-0.00173313 0.08287442 -0.30545663 -0.43281115]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.09591150195400469
gradients["da0"].shape = (5, 10)
gradients["dWf"][3][1] = 0.0
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = -0.062451768586453626
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = -0.0002859524353767697
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = -0.0024024489673653724
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [0.]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.01339511]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [-0.21783941]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [0.22190701]
gradients["dbo"].shape = (5, 1)
Expected Output:
| **gradients[“dx”][1][2]** = | [-0.00173313 0.08287442 -0.30545663 -0.43281115] |
| **gradients[“dx”].shape** = | (3, 10, 4) |
| **gradients[“da0”][2][3]** = | -0.095911501954 |
| **gradients[“da0”].shape** = | (5, 10) |
| **gradients[“dWf”][3][1]** = | -0.0698198561274 |
| **gradients[“dWf”].shape** = | (5, 8) |
| **gradients[“dWi”][1][2]** = | 0.102371820249 |
| **gradients[“dWi”].shape** = | (5, 8) |
| **gradients[“dWc”][3][1]** = | -0.0624983794927 |
| **gradients[“dWc”].shape** = | (5, 8) |
| **gradients[“dWo”][1][2]** = | 0.0484389131444 |
| **gradients[“dWo”].shape** = | (5, 8) |
| **gradients[“dbf”][4]** = | [-0.0565788] |
| **gradients[“dbf”].shape** = | (5, 1) |
| **gradients[“dbi”][4]** = | [-0.06997391] |
| **gradients[“dbi”].shape** = | (5, 1) |
| **gradients[“dbc”][4]** = | [-0.27441821] |
| **gradients[“dbc”].shape** = | (5, 1) |
| **gradients[“dbo”][4]** = | [ 0.16532821] |
| **gradients[“dbo”].shape** = | (5, 1) |
Congratulations !
Congratulations on completing this assignment. You now understand how recurrent neural networks work!
Lets go on to the next exercise, where you’ll use an RNN to build a character-level language model.
PS: 欢迎扫码关注公众号:「SelfImprovementLab」!专注「深度学习」,「机器学习」,「人工智能」。以及 「早起」,「阅读」,「运动」,「英语 」「其他」不定期建群 打卡互助活动。