数据结构笔记8 二叉搜索树（查找、插入、删除）

（笔记总结自浙江大学数据结构MOOC）

二叉搜索树的概念

二叉搜索树（BST，Binary Search Tree），也称二叉排序树或二叉查找树。
二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质：

1. 非空左子树的所有键值小于其根结点的键值。
2. 非空右子树的所有键值大于其根结点的键值。
3. 左、右子树都是二叉搜索树。

二叉搜索树操作的特别函数：
Position Find( ElementType X, BinTree BST )：从二叉搜索树BST中查找元素X，返回其所在结点的地址；
Position FindMin( BinTree BST )：从二叉搜索树BST中查找并返回最小元素所在结点的地址；
Position FindMax( BinTree BST ) ：从二叉搜索树BST中查找并返回最大元素所在结点的地址。
BinTree Insert( ElementType X, BinTree BST )
BinTree Delete( ElementType X, BinTree BST )

二叉搜索树的查找

查找从根结点开始，如果树为空，返回NULL
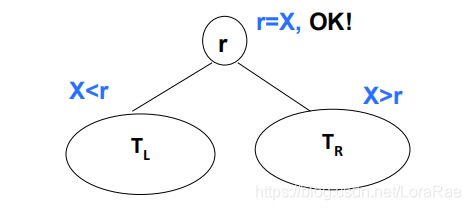
若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：
1.若X小于根结点键值，只需在左子树中继续搜索；
2.如果X大于根结点的键值，在右子树中进行继续搜索；
3.若两者比较结果是相等，搜索完成，返回指向此结点的指针。

Position Find( ElementType X, BinTree BST ) {
if( !BST ) return NULL; /*查找失败*/
if( X > BST->Data )
 return Find( X, BST->Right ); /*在右子树中继续查找*/
Else if( X < BST->Data )
 return Find( X, BST->Left ); /*在左子树中继续查找*/
else /* X == BST->Data */
 return BST; /*查找成功，返回结点的找到结点的地址*/ }

（return Find( X, BST->Right )，return Find( X, BST->Left )，都是“尾递归”）
由于非递归函数的执行效率高，可将“尾递归”函数改为迭代函数

Position IterFind( ElementType X, BinTree BST ) {
 while( BST ) {
 if( X > BST->Data )
 BST = BST->Right; /*向右子树中移动，继续查找*/
 else if( X < BST->Data )
 BST = BST->Left; /*向左子树中移动，继续查找*/
 else /* X == BST->Data */
 return BST; /*查找成功，返回结点的找到结点的地址*/
 }
 return NULL; /*查找失败*/ }

查找的效率决定于树的高度

查找最大和最小元素
最大元素一定是在树的最右分枝的端结点上
最小元素一定是在树的最左分枝的端结点上

若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最小值一定在叶结点上，最大值不一定在叶结点上。

查找最小元素的递归函数

Position FindMin( BinTree BST ) {
 if( !BST ) return NULL; /*空的二叉搜索树，返回NULL*/
 else if( !BST->Left )
 return BST; /*找到最左叶结点并返回*/
 else
 return FindMin( BST->Left ); /*沿左分支继续查找*/ }

查找最大元素的迭代函数

Position FindMax( BinTree BST ) {
 if(BST )
 while( BST->Right ) BST = BST->Right;
 /*沿右分支继续查找，直到最右叶结点*/
 return BST;
}

二叉搜索树的插入

〖分析〗关键是要找到元素应该插入的位置，可以采用与Find类似的方法

BinTree Insert( ElementType X, BinTree BST ) {
 if( !BST ){
 /*若原树为空，生成并返回一个结点的二叉搜索树*/
 BST = malloc(sizeof(struct TreeNode));
 BST->Data = X;
 BST->Left = BST->Right = NULL;
 }else /*开始找要插入元素的位置*/
 if( X < BST->Data )
 BST->Left = Insert( X, BST->Left);
 /*递归插入左子树*/
 else if( X > BST->Data )
 BST->Right = Insert( X, BST->Right);
 /*递归插入右子树*/
 /* else X已经存在，什么都不做 */
 return BST; }

二叉搜索树的删除

考虑三种情况：
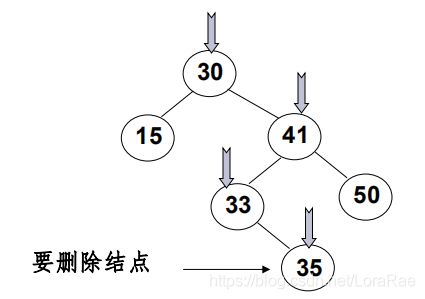
1.要删除的是叶结点：
直接删除，并再修改其父结点指针—置为NULL
〖例〗：删除 35

2.要删除的结点只有一个孩子结点:
将其父结点的指针指向要删除结点的孩子结点
〖例〗：删除 33

3.要删除的结点有左、右两棵子树：
用另一结点替代被删除结点：右子树的最小元素或者左子树的最大元素
〖例〗：删除 41

BinTree Delete( ElementType X, BinTree BST ) 
{ Position Tmp; 
 if( !BST ) printf("要删除的元素未找到"); /* 树空 */
 else if( X < BST->Data ) 
 BST->Left = Delete( X, BST->Left); /* 左子树递归删除 */
 else if( X > BST->Data ) 
 BST->Right = Delete( X, BST->Right); /* 右子树递归删除 */
 else /*找到要删除的结点 */ 
 if( BST->Left && BST->Right ) { /*被删除结点有左右两个子结点 */ 
 Tmp = FindMin( BST->Right ); 
 /*在右子树中找最小的元素填充删除结点*/
 BST->Data = Tmp->Data; 
 BST->Right = Delete( BST->Data, BST->Right);
 /*在删除结点的右子树中删除最小元素*/
 } else { /*被删除结点有一个或无子结点*/
 Tmp = BST; 
 if( !BST->Left ) /* 有右孩子或无子结点*/
 BST = BST->Right; 
 else if( !BST->Right ) /*有左孩子或无子结点*/
 BST = BST->Left;
 free( Tmp );
 }
 return BST;
}