栈和队列习题二
目录
一、实现一个栈,要求实现Push(入栈)、Pop(出栈)、Min(返回最小值)的时间复杂度为O(1)
二、元素出栈、入栈顺序的合法性。如入栈的序列(1,2,3,4,5),出栈序列为 (4,5,3,2,1)
三、一个数组实现两个栈(共享栈)
注:以上三个题的完整代码至 GitHub 查看:https://github.com/lxt-cn/DSCode/tree/master/QueueStackTwo
一、实现一个栈,要求实现Push(入栈)、Pop(出栈)、Min(返回最小值)的时间复杂度为O(1)
1、定义
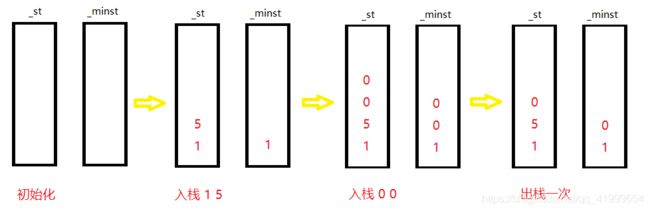
思路:使用两个栈来实现,一个栈用来正常出入栈,另一个栈用来存放最小值。如下图:
typedef int MSTDataType;
typedef struct MinStack
{
Stack _st; // 正常出入栈
Stack _minst; // 最小栈
}MinStack;2、Push(入栈)
思路:正常栈正常入栈即可,需注意,如果入栈元素小于最小栈的栈顶元素,那么入栈元素也入最小栈,即最小栈的栈顶元素始终存放最小值。
void MinStackPush(MinStack* pms, MSTDataType d)
{
assert(pms);
StackPush(&pms->_st, d); // 正常栈入栈
// 1、最小栈为空,说明最小栈中目前没有存放最小值,则入栈元素为最小值
// 2、最小栈的栈顶元素大于入栈元素,说明最小栈栈顶元素需要更新
// 以上两种情况,解决办法都是讲入栈元素给最小栈中也入一份
if (StackEmpty(&pms->_minst) == 0
|| StackTop(&pms->_minst) >= d)
{
StackPush(&pms->_minst, d);
}
}3、Pop(出栈)
思路:和入栈类似,正常栈正常出栈即可,需注意出栈的元素是否为最小栈中的栈顶元素,即出栈的元素是否为目前所有元素中的最小值,如果是最小值,则最小栈也出栈,如果不是,最小栈不动。
void MinStackPop(MinStack* pms)
{
assert(pms);
// 判断出栈元素是否为最小栈中的栈顶元素(即最小值)
// 是,都出栈
// 不是,最小栈不动
if (StackTop(&pms->_st) == StackTop(&pms->_minst))
{
StackPop(&pms->_minst);
}
StackPop(&pms->_st);
}4、Min(返回最小值)
思路:这个就很简单,栈中最小值即最下栈的栈顶元素,直接返回最小栈中的栈顶元素即可。
MSTDataType MinStackMin(MinStack* pms)
{
assert(pms);
return StackTop(&pms->_minst);
}二、元素出栈、入栈顺序的合法性。如入栈的序列(1,2,3,4,5),出栈序列为 (4,5,3,2,1)
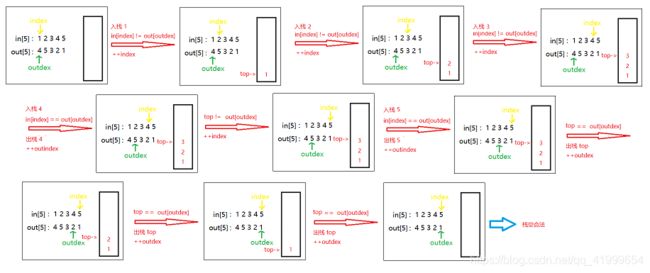
思路:判断一个序列是否可以成为另一个序列的出栈顺序,首先,第一个就是必须两个序列个数相同,如果个数不同,一定不是合法顺序;然后,我们需要做的就是依次比较,即入栈序列按入栈顺序依次和出栈序列进行比较,不同就入栈,相同就出栈,然后出栈序列中下一个数字与此时栈顶元素进行比较,最后只需判断入栈序列是否为空,空则合法,非空则不合法。图解如下:
// 非法 0 合法 1
int IsLegalStackOrder(int* in, int insize, int* out, int outsize)
{
assert(in && out && insize == outsize);
Stack st;
StackInit(&st);
int inindex = 0;
int outindex = 0;
while (inindex < insize)
{
StackPush(&st, in[inindex]);
++inindex;
while (StackEmpty(&st)
&& StackTop(&st) == out[outindex])
{
StackPop(&st);
++outindex;
}
}
if (StackEmpty(&st) == 0)
{
StackDestory(&st);
return 1;
}
StackDestory(&st);
return 0;
}三、一个数组实现两个栈(共享栈)
思路:一个数组实现两个栈,有很多种办法,比如说,第一种办法:将一个数组从中间一分为二,一半是一个栈;第二种办法:将数组从头到尾开始为第一个栈,从尾到头开始为第二个栈,第三种,就是奇数为存放的是第一个栈,偶数位存放的是第二个栈。前两种办法都不能很好地扩容,因此我们在这里只说第三种,即奇偶栈实现共享栈。
1、定义
#define N 100
typedef int SSDataType;
typedef struct ShareStack
{
SSDataType _a[N];
int _top1; // 奇数栈
int _top2; // 偶数栈
}ShareStack;2、入栈
思路:首先判断给哪一个栈入栈,确定入栈的栈为哪一个以后,先判断这个栈是否满了,满了就不再入栈,直接返回,不满就入栈,然后 top+=2 。
void ShareStackPush(ShareStack* pss, SSDataType d, int which)
{
assert(pss && which == 1 || which == 2);
if (which == 1)
{
if (pss->_top1 >= N)
{
printf("Stack1 Full\n");
return;
}
pss->_a[pss->_top1] = d;
pss->_top1 += 2;
}
else if (which == 2)
{
if (pss->_top2 >= N)
{
printf("Stack2 Full\n");
return;
}
pss->_a[pss->_top2] = d;
pss->_top2 += 2;
}
else
{
printf("StackPush Error\n");
return;
}
}3、出栈
思路:与入栈思路相同,先判断是哪个栈出栈,在判断栈是否为空,空直接返回,不空则出栈,top-=2 。
void ShareStackPop(ShareStack* pss, int which)
{
assert(pss && which == 1 || which == 2);
if (which == 1)
{
if (pss->_top1 == 0)
{
printf("Stack1 Empty\n");
return;
}
pss->_top1 -= 2;
}
else if (which == 2)
{
if (pss->_top2 == 1)
{
printf("Stack2 Empty\n");
return;
}
pss->_top2 -= 2;
}
else
{
printf("StackPop Error\n");
return;
}
}4、取栈顶元素
思路:与之前相同,先判断是哪个栈,再判断是否为空,空返回 -1 ,非空,则直接返回 top 位置的元素。
SSDataType ShareStackTop(ShareStack* pss, int which)
{
assert(pss && which == 1 || which == 2);
if (which == 1)
{
if (pss->_top1 == 0)
{
printf("Stack1 Empty\n");
return -1;
}
return pss->_a[pss->_top1 - 2];
}
else if (which == 2)
{
if (pss->_top2 == 1)
{
printf("Stack2 Empty\n");
return -1;
}
return pss->_a[pss->_top2 - 2];
}
else
{
printf("Get StackTop Error\n");
return -1;
}
}