查找——平衡二叉树Balanced Binary/Height-Balanced Tree的详解与实现
查找
- 8.5 平衡二叉树
- 8.5.1 平衡二叉树的定义
- 8.5.2 平衡旋转
- 8.5.3 插入结点
- 8.5.4 删除结点
- 其他
8.5 平衡二叉树
在二叉排序树上实现查找的时间复杂度与从根到所查数据元素的结点的路径长度成正比,在最坏情况下这个长度等于树的高度。在构造二叉排序树时,如果输入的数据元素序列恰巧按其关键字大小有序,则在形式上已经退化成一个单链表了。这样查找操作所需要的时间就是O(n),或者说与结点个数成线性关系。
因此需要有一种方法来避免使二叉排序树变得过于窄而高这种情况的发生。如果能够保证树的高度与树中结点数目n之间成log2 n 关系,就能提高查找效率。
8.5.1 平衡二叉树的定义
- 一棵平衡二叉树或者是空树,或者是具有下列性质的二叉排序树:
它的左子树和右刊都是平衡二叉树,且左子树和右子树的高度之差的绝对值不超过1。
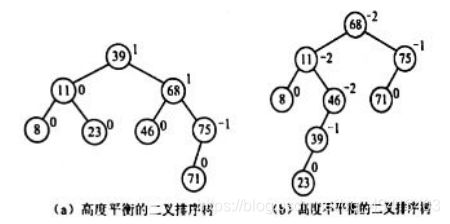
在图8-14(a)标的二叉排序树中,没有一个结点的左子树和右子树高度之差的绝对值超过1,因此它是一棵平衡二叉树。而在图8-14(b)所示的二叉排序树中,根的右子树的高度为1。而左子树的高度为4,两者高度之差的绝对值为2,因此它不是一棵平衡二叉树。 - 平衡因子(balance factor,BF):每个结点右子树的高度减去左子树的高度所得的高度差。
- 根据平衡二叉树的定义,任一结点的平衡因子只能是-1、0和1。如果有结点的平衡因子的绝对值大于1,(裸二叉排序树就失去了平衡,就不是平衡二叉树了。
- 一棵具有n个结点的平衡二叉树,其平均查找长度为O(log2n)。
8.5.2 平衡旋转
- 假定向平衡二叉树中插入一个新结点后破坏了它的平衡性,首先需要找到插入新结点后失去平衡的最小子树的根结点,然后对它进行相应的旋转,使之成为新的平衡子树。
- 当失去平衡的最小子树被调整为平衡子树后,整个二叉排序树就又平衡了。在平衡调整过程中除失去平衡的最小子树外,其他结点不需要做任何调整。
- 失去平衡的最小子树的根是离插入点最近,且平衡因子的绝对值大于1的结点。设失去平衡的最小子树的根为A。则平衡调整可有以下四种情况:
(1)LL平衡旋转
如果因为在A的左孩子B的左子树上插入新结点,使A的平衡因子由-1变成-2,则需进行LL平衡旋转。

图(a)为原始的平衡状态,图(b)为插入结点X后不平衡的状态。
为使树恢复平衡,从A沿刚才插入路径连续取两个结点A和B,以结点B为旋转轴,将结点A顺时针向下旋转成为B的右孩子,结点B代替原来结点A的位置,结点B原来的右孩子作为结点A的左孩子。
template<class ElemType> AVLNode<ElemType>* AVL<ElemType>::LL(AVLNode<ElemType> *t)
{
AVLNode<ElemType> *q=t->left;
t->left=q->right;
q->right=t;
t=q;
t->height=max(GetHeight(t->left),GetHeight(t->right))+1;
q->height=max(GetHeight(q->left),GetHeight(q->right))+1;
return q;
}
(2)RR平衡旋转
如因为在A的右孩子B的右子树上插入新结点,使A的平衡因子由1变成2,则需进行RR平旋转。

为使树恢复平衡,从A沿刚才的插入路径连续取两个结点A和B,以结点B为旋转轴,将结点A逆时针向下旋转成为B的左孩子,结点B代替原来结点A的位置,结点B原来的左孩子成为结点A的右孩子。
template<class ElemType> AVLNode<ElemType>* AVL<ElemType>::RR(AVLNode<ElemType> *t)
{
AVLNode<ElemType> *q=t->right;
t->right=q->left;
q->left=t;
t=q;
t->height=max(GetHeight(t->left),GetHeight(t->right))+1;
q->height=max(GetHeight(q->left),GetHeight(q->right))+1;
return q;
}
(3)LR平衡旋转
如果是因为在A的左孩子B的右子树上插入新结点,使A的平衡因子由-1变成-2,则需要进行LR平旋转。

为使二叉排序树恢复平衡,则需要进行先逆时针后顺时针的平衡旋转,即先将A的左孩子B的右孩子C向逆时针方向旋转代替B的位置,再以结点C为旋转轴,将结点A向顺时针方向旋转成为C的右孩子,结点C代替原来结点A的位置,结点C原来的左孩子转为结点B的右孩子,结点C原来的右孩子转为结点A的左孩子。
template<class ElemType> AVLNode<ElemType>* AVL<ElemType>::LR(AVLNode<ElemType> *t)
{
//对p的左节点进行RR旋转,再对根节点进行LL旋转
AVLNode<ElemType> *q=RR(t->left);
t->left=q;
return LL(t);
}
(4)RL平衡旋转
如果是因为在A的右孩子B的左子树上插入新结点,使A的平衡因子由1变成2,则需要进行RL平衡旋转。

为使树恢复平衡,则需要进行先顺时针后逆时针的平衡旋转,即先将A的右孩子B的左孩子C向顺时针方向旋转代替B的位置,再以结点C为旋转轴,将结点A向逆时针方向旋转成为C的左孩子,结点C代替原来结点A的位置,结点C原来的左孩子转为结点A的右孩子,结点C原来的右孩子转为结点B的左孩子。
template<class ElemType> AVLNode<ElemType>* AVL<ElemType>::RL(AVLNode<ElemType> *t)
{
//对p的左节点进行RR旋转,再对根节点进行LL旋转
AVLNode<ElemType> *q=LL(t->right);
t->right=q;
return RR(t);
}
8.5.3 插入结点
在平衡二叉树中插入一个新结点后,如果二叉排序树中某个结点的平衡因子的绝对值|bf|>1,则出现了不平衡,这时需要根据平衡旋转的类型立即进行平衡化处理,使得二叉排序树中各结点重新平衡。平衡二叉树插入结点的算法思想如下。
1)按二叉排序树的性质插入结点。
2)如果插入结点之后出现不平衡的结点,则转步骤3);否则插入完成。
3)找到失去平衡的最小子树。
4)判断平衡旋转的类型作相应平衡化处理。
在插入之后如果树上出现平衡因子绝对值大于1的结点,则说明二叉排序树已不平衡。这时失去平衡的最小子树的根结点必为离插入结点最近,而且插入之前平衡因子绝对值为1的结点。为此,要解决上述三个问题可以作如下处理。
1)在查找结点x的插入位置的过程中,记下从根结点到插入位置的路径上离插入位置最近的且平衡因子绝对值为1的结点,并令指针a指向该结点;如果此路径上不存在平衡因子绝对值为1的结点,则指针a指向根结点。
2)对于从a结点到x结点的路径上的每一个结点(不包括结点x),根据结点中关键字和x的大小比较修改结点的平衡因子。如果结点关键字大于x,则结点平衡因子减1;否则结点平衡因子加1。
3)如果结点a的平因子绝对值为2,则表示二叉排序树失去平衡,再根据结点a及其左右孩子的平衡因子值来确定平衡旋转的类型。
#define LH -1
#define EH 0
#define RH 1
template<class ElemType> AVLNode<ElemType>*
AVL<ElemType>::Find(const ElemType &key,AVLNode<ElemType> *&f,AVLNode<ElemType> *&a,AVLNode<ElemType> *&af)
{
AVLNode<ElemType> *p=root;//p为搜索指针
a=af=f=NULL;//初始化
while(p!=NULL && p->data!=key)
{
if(p->bf !=EH)
{
af=f;
a=p;
}
if(key < p->data)//key比p小,在左子树上进行查找
{
f=p;
p=p->left;
}
else
{
f=p;
p=p->right;
}
}
if(a==NULL)
a=root;
return p;
}
算法先利用上面的 Find()函数查找插入位咒,再根据a结点的平衡因子(bf) 以及插入元素值与a结点元素值比较关系确定平衡旋转的方式。
结点a的平衡因子有以下三种情况。
1)结点a的bf为-1:此时,如果被插入元素的值小于a的值,就会使结点a的平衡因子从-1变为-2。因此需要进行LL或LR旋转;否则,被插入元素的值大于a的值,就会使结点a的平衡因子从-1变为0。所以不需要进行平衡旋转,但需要修改从结点a到结点p这条路径上各结点的平衡因子。要区分LL还是LR旋转,就要比较被插入元素p的值和a的左孩子结点b的值,如果p的值小于b的值,就要进行LL旋转,否则进行LR旋转。
2)结点a的bf为0:此时,插入元素后a的平衡因子会变为-1(被插入元素的值小于a的值)或1(被插入元素的值大于a的值),所以不需要进行平衡旋转,但需要修改从结点a到结点p这条路径上各结点的平衡因子。
3)结点a的bf为1:此时,如果被插入元素的值大于a的值,就会使结点a的平衡因子从|变为2,因此需要进行RR或RL旋转;否则,被插入元素的值小于a的值,就会使结点a的平衡因子从1变为0,所以不需要进行平衡旋转,但需要修改从结点a到结点p这条路径上各结点的平衡因子。要区分RR还是RL旋转,就要比较被插入元素p的值和a的右孩子结点的值,如果p的值大于b的值,就要进行RR旋转;否则进行RL旋转。
另外,如果在调用 Find()函数进行查找时,在平衡二叉树中找到了相应元素,就不需要进行插入操作。
template<class ElemType> void
AVL<ElemType>::FindParent(const ElemType &x,AVLNode<ElemType> *&p)
{
AVLNode<ElemType> *r=root;
p=NULL;
while(r!=NULL && r->data!=x)
{
if(x < r->data)
{
p=r;
r=r->left;
}
else
{
p=r;
r=r->right;
}
}
}
template<class ElemType> void
AVL<ElemType>::Insert(AVLNode<ElemType> *&t,const ElemType &x)
{
if(t==NULL)
t=new AVLNode<ElemType>(x);
else if(x < t->data)
{
Insert(t->left,x);
//判断平衡情况
if(GetHeight(t->left) - GetHeight(t->right) >1)
{
//分两种情况,左左或右右
if(x < t->left->data)//左左
t=LL(t);
else
t=LR(t);
}
}
else if(x > t->data)
{
Insert(t->right,x);
if(GetHeight(t->right)-GetHeight(t->left) >1)
{
if(x > t->right->data)
t=RR(t);
else
t=RL(t);
}
}
//else 数据重复
t->height=max(GetHeight(t->left),GetHeight(t->right))+1;
}
template<class ElemType> void AVL<ElemType>::Insert(ElemType x)
{
AVLNode<ElemType> *p;
FindParent(x,p);
Insert(p,x);
}
8.5.4 删除结点
在平衡二叉树上进行删除操作时,同样也需要考虑平衡化旋转问题。当删除结点x后,需要对从结点x的双亲到根结点的路径上这些结点进行考虑其子树的变化是否影响其平衡因子的值,一旦结点平衡因子的绝对值大于1时,就需要进行相应的平衡化处理。为此在算法中需要定义一个布尔变量isShorter来指明子树的高度是否被缩短。布尔变量isShorter的初始化值为true。在每个结点上要做的平化操作取决于isShortcr的值和结点的平衡因子bf的值,有时还要依赖其孩子的平衡因子。下面给出删除算法的思想。
1)如果被删结点x有左、右孩子,首先找x在中序次序下的直接前驱y(同样也可以找直接后继),再把结点y的内容传送给结点x,再删除结点y(结点y最多有一个孩子)。
2)对于删除最多有一个孩子的结点x,可以简单地把x的双亲结点中原来指向x的指针改指到x的孩子结点。如果结点x没有孩子,则其双亲结点的相应指针置为空。
3)对于从结点x的双亲到根结点的路径上的每一个结点p,当布尔变量 isShorter 的值为true时,根据以下三种不同的情况维续步骤,直到布尔变量 isShorter 的值为 false时,整个删除算法结束。
①情况一,当结点p的平衡因子为0,如果它的左子树或右子树被缩短(isShorter的值为true),则它的平衡因子改为1或-1,由于此时以结点p为根的子树高度没有缩短,所以置isShorter 的值为false。由于p的左子树被缩短,所以p的平衡因子改为1。
②情况二,结点p的平衡因子不为0,且其较高的子树被缩短,则p的平衡因子改为0。由于此时以结点p为根的子树高度被缩短,所以 isShorter 的值仍为true。 开始时p的平衡因子为-1,由于p的左子树高度缩短1,所以最后p的平衡因子为0。
③情况三,结点p的平衡因子不为0,且较矮的子树被缩短,则在结点p发生不平衡。此吋,将进行平衡化旋转来恢复平衡。令结点p的较高子树的根结点为q,则根据结点p和q的平衡因子值,有如下三种平衡化操作:
- 如果q的平衡因子为0,则只要执行一个单旋转就可恢复结点p的平衡,由于旋转后被处理子树的高度没有缩短,所以置isShorter 的值为false。
- 如果q的平衡因子与p的平衡因子的符号相同,则只要执行一个单旋转就可恢复结点p的平衡。由于此时被处理子树的高度被缩短,所以isShorter 的值仍为true。最后,结点p和q的平衡因子均改为0。
- 如果p与q的平衡因子的符号相反,则需要执行一个双旋转来恢复平衡,先围绕q转、再围绕p转。由于此时被处理子树的高度被缩短,所以 isShorter 的值仍为true,新的根结点的平衡因子置为0,其他结点的平衡因子作相应处理。


template<class ElemType> bool
AVL<ElemType>::Contains(const ElemType x)const
{
AVLNode<ElemType> *t=root;
while(t!=NULL && t->data!=x)
{
if(x < t->data)
t=t->left;
else if(x > t->data)
t=t->right;
}
if(t!=NULL)
return true;
else
return false;
}
template<class ElemType> bool
AVL<ElemType>::Delete(AVLNode<ElemType> *&t,const ElemType x)
{
//t为空,未找到要删除的结点
if(t==NULL)
return false;
if(t->data == x)
{
//左右子树都非空
if(t->left!=NULL && t->right!=NULL)
{
//在高度更大的那个子树上进行删除操作
//左子树高度达,删除左子树中值最大的结点,将其赋值给根节点
if(GetHeight(t->left)>GetHeight(t->right))
{
t->data=FindMax(t->left)->data;
Delete(t->left,t->data);
}
else//右子树高度更大,删除右子树中值最小的结点,将其赋值给根节点
{
t->data=FindMin(t->right)->data;
Delete(t->right,t->data);
}
}
else
{
//左右子树有一个不为空,直接用需要删除的结点的子节点替换即可
AVLNode<ElemType> *old=t;
t= (t->left)?t->left:t->right;//t赋值为不空的子节点
delete old;
}
}
else if(x < t->data)//要删除的结点在左子树上
{
//递归删除左子树上的结点
Delete(t->left,x);
//判断是否仍然满足平衡条件
if(GetHeight(t->right)-GetHeight(t->left) > 1)
{
if(GetHeight(t->right->left) > GetHeight(t->right->right))
{
//RL双旋转
t=RL(t);
}
else
{
//RR单旋转
t=RR(t);
}
}
else
{
//满足平衡条件,调整高度信息
t->height = max(GetHeight(t->left),GetHeight(t->right))+1;
}
}
else//要删除的结点在右子树上
{
//递归删除右子树结点
Delete(t->right,x);
//判断平衡情况
if(GetHeight(t->left)-GetHeight(t->right) > 1)
{
if(GetHeight(t->left->right) > GetHeight(t->left->left))
{
//LR双旋转
t=LR(t);
}
else
{
//LL单旋转
t=LL(t);
}
}
else//满足平衡性 调整高度
{
t->height = max(GetHeight(t->left),GetHeight(t->right))+1;
}
}
return true;
}
template<class ElemType> bool AVL<ElemType>::Delete(ElemType x)
{
if(Contains(x)==true)
{
cout<<"查找到"<<x<<",进行删除"<<endl;
return Delete(root,x);
}
else
{
cout<<"值为"<<x<<"的结点不存在"<<endl;
return false;
}
}
说明:文中代码参考https://blog.csdn.net/yangguang0012/article/details/82878326。
其他
在平衡二叉排序树的每个结点中增设一个lsize域,其值为该结点左子树中的节点数加一。写一个时间复杂度为O(log2n)的算法,确定树中第k小结点的位置。
(1)结点类
template<class ElemType> class AddAVLNode
{
public:
ElemType data;
int lsize;
int bf;
AddAVLNode<ElemType> *left,*right;
AddAVLNode()
{
bf=0;
lsize=0;
left=right=NULL;
}
AddAVLNode(ElemType d,int binfactor=0,int ls=0,AddAVLNode<ElemType> *leftchild=NULL,AddAVLNode<ElemType> *rightchild=NULL)
{
data=d;
bf=binfactor;
lsize=ls;
left=leftchild;
right=rightchild;
}
};
(2)一些操作
#include "AddBalancedSortNode.h"
#include