讲清迪杰斯特拉（DIJKSTRA）算法，附python代码

最近有个同事问我迪杰斯特拉算法，以前都是直接用，三个循环体直接一套就出来，具体逻辑懒得去理解，这次被问到，就花了点时间理了理算法的底层逻辑。

---------

迪杰斯特拉算法是搜索出所有点到起点的最短距离。

怎么找？

第一步，找出距离V0最近距离的点，设为V2。(显然此时V2的最短路径已经找到，就是V2直达路径。)

第二步，以V2为中转点mid_Node,用m替代

（Lx0,表示Vx到V0的距离，Lxm表示Vx到mid_Node的距离，其他同理）

第三步，取其他任意点Vx，比较Lx0和Lxm+Lm0的大小，令cost[X]=min（Lx0，LXm+Lm0）,即找到了点x到0的更短路径，并更新进cost数组里。（其实就是让其他点尝试以mid_Node为中转，能否缩短路径，若能，就更新最短路径。）在for循环里把所有的点都尝试一遍中转方案，并把最短路径更新。(对应代码里 for NEXT_Node in range(lenth):循环体的内容)

第四步，搜索cost数组里的最短路径（除被选为mid_Node的点外，点是否选过为mid_Node是用数组v[]做标记，在if语句中判断，V[X]代表X是否已找到最短路径，1是，0不是。实际上被选为mid_Node就表示该点已经找到抵达V0的最短路径。这个等下会解释，先把流程弄清）

第五步，把第三步里搜索到最短路径的端点设置为mid_Node，并且在V数组里把该端点的标志位置1.

第六步，判断是否所有点都设置为过mid_Node,是则结束，否则跳转到第三步。

--------

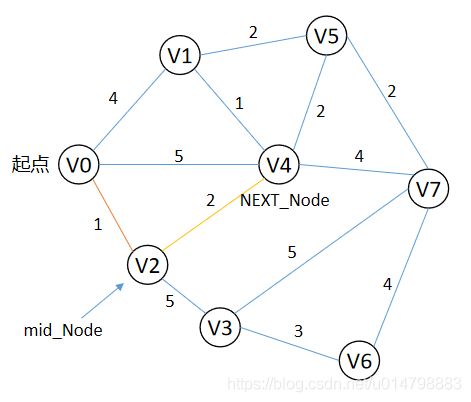
结合图片走一下步骤

 

贴一下几个代码会用到的数组变量

    cost[i] 表示V0到Vi的已知最短路径长度
    mid_Node:中转点，以已求得V0到Vi的最短路径的Vi作为中转点。
    NEXT_Node:尝试优化的点，以中转点为中心，检测NEXT_Node直达V0方案，和经过mid_Node中转到V0的方案哪个更优
    check_Node:索引，搜索cost数组里最短路径的点，最短的点会赋值给mid_Node,作为中转点。

    V数组用来存放标志位，表示是否已经找到x点的最短路径，找到则V[x]=1,否则为0，这是为了避免陷入死循环，一直卡在第一条最短路径出不来。

 

cost数组初始化时是所有点到V0的距离，即cost=[0,4,1,max,5,max,max,max]

第一步，显然选中V2，

第二步，V2作为中转点，

第三步，尝试优化其他点，其他点把中转点作为中转，比较能否缩短到V0的距离，这里能看到，V4经过V2中转后，到V0距离短了由5变为3，V3由无穷远变为6，其他点经过V2中转反而更长（变为无法抵达，即无穷远，因为其他点无法直达V2，到V2的距离是max）。把优化后的值更新进cost数组。

此时cost=[0,4,1,6,3,max,max,max]

第四步，选取cost数组里除cost[0],cost[2]以外最短的路径，显然是3，即cost[4],取得的端点是V4

第五步，把V4作为中转点，并把V数组的标志位置1，表示已找到V4的最短路径。

第六步，跳转到第三步循环，直到所有点都找到最短路径。

 

 

前面遗留的问题：被选为mid_Node就表示该点已经找到抵达V0的最短路径

这也是迪杰斯特拉算法里最绕的一个地方-----凭什么确定这个点已经找到了最短路径？

迪杰斯特拉算法的核心思想就是每次选mid_Node都是取cost数组待探索点里距离最小的（ for check_Node in range(lenth):循环里做的）。也就是说，这条路径在剩下其他已知路径里已经是最小了，没法再优化了。为什么说没法优化了？

因为唯一可行的优化方法就是用比该点Vx到V0的路径Lx0更短的路径Lm0作为中转，中转距离就是Lxm+L0m，（这个路径优化就是for NEXT_Node in range(lenth)循环里做的事，选取mid_Node前已经做完了，所以可行的优化方法已经优化过了），

剩下的所有优化方案，只剩下用比Lx0（或Lm0+Lxm，取决于哪个更小）更长的路径作为中转。这显然是绕弯路了，必然增加长度，没必要尝试，所以没法再优化了，故得到的就是Vx到V0的最短路径。

 

 

python代码实现如下：

代码和前文示例的图片不对应，图片是随手画的，强迫症可以复制一下代码改一下数组和cost，path，range的长度，就能对应到图片了

def dijkstra(graph, start_Node, path, cost, max):
    """
    graph：二维数组，就是用行列坐标表示图形上两点之间的距离。
    start_Node：起始点
    path[i] 表示vi节点的前一个节点，即中转点。
    cost[i] 表示V0到Vi的已知最短路径长度
    mid_Node:中转点，以已求得V0到Vi的最短路径的Vi作为中转点。
    NEXT_Node:尝试优化的点，以中转点为中心，检测NEXT_Node直达V0方案，和经过mid_Node中转到V0的方案哪个更优
    check_Node:索引，搜索cost数组里最短路径的点，最短的点会赋值给mid_Node,作为中转点。

    """
    lenth = len(graph)
    v = [0] * lenth  # V数组初始化为0，用于标记该点是否已取得最短路径
    # 初始化 path，cost，V
    for i in range(lenth):
        if i == start_Node:
            v[start_Node] = 1
        else:
            cost[i] = graph[start_Node][i]  # cost获取起点至其他点的直达权重
            path[i] = (start_Node if (cost[i] < max) else -1)  # 前置点为起点或-1（无法直达起点）

    # print v, cost, path
    for i in range(1, lenth):  # 遍历的数等于除去起点的点的数量
        minCost = max  # 初始值取最大
        mid_Node = -1
        for check_Node in range(lenth):  # 搜索一个到起点V0最近的点，作为中转点mid_Node
            if v[check_Node] == 0 and cost[check_Node] < minCost:  # mid_Node点未取得最短路径，且路径权重小于最小值，则获取w，也就是先取得
                minCost = cost[check_Node]
                mid_Node = check_Node

        if mid_Node == -1: break  # 找不到权重小于max的点
        # 剩下都是不可通行的节点，跳出循环
        v[mid_Node] = 1  # check_Node已取得最短路径
        for NEXT_Node in range(lenth):
            if v[NEXT_Node] == 0 and (graph[mid_Node][NEXT_Node] + cost[mid_Node] < cost[NEXT_Node]):  # 检查所有未遍历的点NEXT_Node，检测前面获取的mid_Node对NEXT_Node的影响
                cost[NEXT_Node] = graph[mid_Node][NEXT_Node] + cost[mid_Node]  # 更新权值
                path[NEXT_Node] = mid_Node  # 更新路径
        # for 更新其他节点的权值（距离）和路径
    return path


if __name__ == '__main__':
    max = 999999  # max即表示为无法直达
    graph = [
        [5, max, 10, max, 30, 100],
        [max, max, 5, max, max, max],
        [max, 15, max, 50, max, max],
        [max, max, max, max, max, 10],
        [max, max, max, 20, max, 60],
        [max, 15, max, max, max, max],
    ]
    path = [0] * 6
    cost = [0] * 6
    print(dijkstra(graph, 0, path, cost, max))
    print(cost)