机器学习概率基础-高斯分布相关重要知识推导
文章目录
- 高斯分布的最大似然估计
- 参数均值与方差的有偏无偏估计
- 关于均值的无偏估计
- 关于方差的有偏估计
- 二维高斯分布的可视化探究
- 高斯分布的局限性
- 求多维高斯分布的边缘分布和条件概率分布
高斯分布的最大似然估计
数据 X = ( x 1 , ⋯ , x N ) ⊤ = ( x 1 ⊤ ⋮ x N ⊤ ) N × p , x i ∈ R P , x i ∼ iid N ( μ , Σ ) X=\left(x_{1}, \cdots, x_{N}\right)^{\top}=\left(\begin{array}{c}{x_{1}^{\top}} \\ {\vdots} \\ {x_{N}^{\top}}\end{array}\right)_{N \times p},x_{i} \in \mathbb{R}^{P}, \quad x_{i} \stackrel{\text { iid }}{\sim} N(\mu, \Sigma) X=(x1,⋯,xN)⊤=⎝⎜⎛x1⊤⋮xN⊤⎠⎟⎞N×p,xi∈RP,xi∼ iid N(μ,Σ)
极大似然估计: θ M L E = a r g m a x θ P ( x ∣ θ ) \theta_{MLE}=argmax_{\theta}P(x|\theta) θMLE=argmaxθP(x∣θ)
高斯分布:
p ( x ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) p(x)=\frac{1}{\sqrt{2\pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) p(x)=2πσ1exp(−2σ2(x−μ)2) 一元高斯
P ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 exp ( − 1 2 ( x − μ ) ⊤ Σ − 1 ( x − μ ) ) P(x)=\frac{1}{(2 \pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left(-\frac{1}{2}(x-\mu)^{\top} \Sigma^{-1}(x-\mu)\right) P(x)=(2π)2n∣Σ∣211exp(−21(x−μ)⊤Σ−1(x−μ)) 多元高斯
一元高斯为例
log P ( x ∣ θ ) = log Π i = 1 N P ( x i ∣ θ ) = Σ i = 1 N log P ( x i ∣ θ ) = Σ i = 1 N log 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) = Σ i = 1 N [ log 1 2 π + log 1 σ − ( x − μ ) 2 2 σ 2 ] \begin{aligned} \log P(x | \theta) &=\log \Pi_{i=1}^{N} P\left(x_{i} | \theta\right)=\Sigma_{i=1}^{N} \log P\left(x_{i} | \theta\right) \\ &=\Sigma_{i=1}^{N} \log \frac{1}{\sqrt{2\pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \\ &=\Sigma_{i=1}^{N}\left[\log \frac{1}{\sqrt{2 \pi}}+\log \frac{1}{\sigma}-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right] \end{aligned} logP(x∣θ)=logΠi=1NP(xi∣θ)=Σi=1NlogP(xi∣θ)=Σi=1Nlog2πσ1exp(−2σ2(x−μ)2)=Σi=1N[log2π1+logσ1−2σ2(x−μ)2]
估计均值:
μ M L E = arg max μ log P ( x ∣ θ ) = arg max μ Σ i = 1 N − ( x − μ ) 2 2 σ 2 = arg max Σ i = 1 N ( x i − μ ) 2 \begin{aligned} \mu_{MLE} &=\arg \max _{\mu} \log P(x | \theta) \\ &=\arg \max _{\mu} \Sigma_{i=1}^{N}-\frac{(x-\mu)^{2}}{2 \sigma^{2}} \\ &=\arg \max \Sigma_{i=1}^{N}\left(x_{i}-\mu\right)^{2} \end{aligned} μMLE=argμmaxlogP(x∣θ)=argμmaxΣi=1N−2σ2(x−μ)2=argmaxΣi=1N(xi−μ)2
∂ ∂ μ Σ ( x i − μ ) 2 = Σ i = 1 N 2 ( x i − μ ) ( − 1 ) = 0 \frac{\partial}{\partial \mu} \Sigma\left(x_{i}-\mu\right)^{2}=\Sigma_{i=1}^{N} 2\left(x_{i}-\mu\right)(-1)=0 ∂μ∂Σ(xi−μ)2=Σi=1N2(xi−μ)(−1)=0
⇒ Σ i = 1 N ( x i − μ ) = 0 ⇒ Σ i = 1 N x i = N μ ⇒ μ M L E = 1 N Σ i = 1 N x i \Rightarrow \Sigma_{i=1}^{N}\left(x_{i}-\mu\right)=0 \Rightarrow \Sigma_{i=1}^{N} x_{i}=N \mu \Rightarrow \mu_{M L E}=\frac{1}{N} \Sigma_{i=1}^{N} x_{i} ⇒Σi=1N(xi−μ)=0⇒Σi=1Nxi=Nμ⇒μMLE=N1Σi=1Nxi
E [ μ M L E ] = 1 N Σ i = 1 N E [ x i ] = 1 N Σ i = 1 N μ = μ E\left[\mu_{M L E}\right]=\frac{1}{N} \Sigma_{i=1}^{N} E\left[x_{i}\right]=\frac{1}{N} \Sigma_{i=1}^{N} \mu=\mu E[μMLE]=N1Σi=1NE[xi]=N1Σi=1Nμ=μ (无偏估计)
估计方差:
σ M L E 2 = arg max log P ( x ∣ θ ) = arg max σ ( − log σ − 1 2 σ 2 ( x i − μ ) 2 ) \begin{aligned} \sigma_{M L E}^{2} &=\arg \max \log P(x | \theta) \\ &=\arg \max _{\sigma}\left(-\log \sigma-\frac{1}{2 \sigma^{2}}\left(x_{i}-\mu\right)^{2}\right) \end{aligned} σMLE2=argmaxlogP(x∣θ)=argσmax(−logσ−2σ21(xi−μ)2)
令 L ( σ ) = ( − log σ − 1 2 σ 2 ( x i − μ ) 2 ) L(\sigma)=\left(-\log \sigma-\frac{1}{2 \sigma^{2}}\left(x_{i}-\mu\right)^{2}\right) L(σ)=(−logσ−2σ21(xi−μ)2)
∂ L ∂ σ = Σ i = 1 N [ − 1 σ + 1 2 ( x i − μ ) ⋅ 2 ⋅ σ − 3 ] = 0 \frac{\partial L}{\partial \sigma}=\Sigma_{i=1}^{N}\left[-\frac{1}{\sigma}+\frac{1}{2}\left(x_{i}-\mu\right) \cdot 2 \cdot \sigma^{-3}\right]=0 ∂σ∂L=Σi=1N[−σ1+21(xi−μ)⋅2⋅σ−3]=0
⇒ Σ i ‾ = 1 N [ − 1 σ + ( x i − μ ) σ − 3 ] = 0 ⇒ Σ i = 1 N [ − σ 2 + ( x i − μ ) ] = 0 ⇒ Σ i = 1 N ( − σ 2 ) + Σ i = 1 N ( x i − μ ) 2 = 0 ⇒ N σ 2 = Σ i = 1 N ( x i − μ ) 2 \begin{array}{l}{\Rightarrow \Sigma_{\overline{i}=1}^{N}\left[-\frac{1}{\sigma}+\left(x_{i}-\mu\right) \sigma^{-3}\right]=0} \\ {\Rightarrow \Sigma_{i=1}^{N}\left[-\sigma^{2}+\left(x_{i}-\mu\right)\right]=0} \\ {\Rightarrow \Sigma_{i=1}^{N}\left(-\sigma^{2}\right)+\Sigma_{i=1}^{N}\left(x_{i}-\mu\right)^{2}=0} \\ {\Rightarrow N \sigma^{2}=\Sigma_{i=1}^{N}\left(x_{i}-\mu\right)^{2}}\end{array} ⇒Σi=1N[−σ1+(xi−μ)σ−3]=0⇒Σi=1N[−σ2+(xi−μ)]=0⇒Σi=1N(−σ2)+Σi=1N(xi−μ)2=0⇒Nσ2=Σi=1N(xi−μ)2
σ M L E 2 = 1 N Σ i = 1 N ( x i − μ M L E ) 2 \sigma_{M L E}^{2}=\frac{1}{N} \Sigma_{i=1}^{N}\left(x_{i}-\mu_{M L E}\right)^{2} σMLE2=N1Σi=1N(xi−μMLE)2(有偏估计)
参数均值与方差的有偏无偏估计
θ = ( μ , σ 2 ) , x i ∼ N ( μ , σ 2 ) \theta=\left(\mu, \sigma^{2}\right), \quad x_{i} \sim N\left(\mu, \sigma^{2}\right) θ=(μ,σ2),xi∼N(μ,σ2)
μ M L E = 1 N Σ i = 1 N x i \mu_{M L E}=\frac{1}{N} \Sigma_{i=1}^{N} x_{i} μMLE=N1Σi=1Nxi (无偏估计)
σ M L E 2 = 1 N Σ i = 1 N ( x i − μ M L E ) 2 \sigma_{M L E}^{2}=\frac{1}{N} \Sigma_{i=1}^{N}\left(x_{i}-\mu_{MLE}\right)^{2} σMLE2=N1Σi=1N(xi−μMLE)2 (有偏估计)
关于均值的无偏估计
E [ μ M L E ] = E [ 1 N Σ i = 1 N x i ] = 1 N Σ i = 1 N E ( x i ) = 1 N ⋅ N ⋅ μ = μ E\left[\mu_{M L E}\right]=E\left[\frac{1}{N} \Sigma_{i=1}^{N} x_{i}\right]=\frac{1}{N} \Sigma_{i=1}^{N} E\left(x_{i}\right)=\frac{1}{N} \cdot N \cdot \mu=\mu E[μMLE]=E[N1Σi=1Nxi]=N1Σi=1NE(xi)=N1⋅N⋅μ=μ
关于方差的有偏估计
σ M L E 2 = 1 N Σ i = 1 N ( x i − μ M L E ) 2 = 1 N Σ i = 1 N ( x i 2 − 2 ⋅ x i ⋅ μ M L E + μ M L E 2 ) \sigma_{M L E}^{2}=\frac{1}{N} \Sigma_{i=1}^{N}\left(x_{i}-\mu_{M L E}\right)^{2} = \frac{1}{N} \Sigma_{i=1}^{N}\left(x_{i}^{2}-2 \cdot x_{i} \cdot \mu_{M L E}+\mu_{M L E}^{2}\right) σMLE2=N1Σi=1N(xi−μMLE)2=N1Σi=1N(xi2−2⋅xi⋅μMLE+μMLE2)
= 1 N Σ i = 1 N x i 2 − 1 N Σ i = 1 N 2 ⋅ x i μ M L E + 1 N Σ i = 1 N μ M L E 2 ~~~~~~~~~~~=\frac{1}{N} \Sigma_{i=1}^{N} x_{i}^{2}-\frac{1}{N} \Sigma_{i=1}^{N} 2 \cdot x_{i} \mu_{M L E}+\frac{1}{N} \Sigma_{i=1}^{N} \mu_{MLE}^{2} =N1Σi=1Nxi2−N1Σi=1N2⋅xiμMLE+N1Σi=1NμMLE2
= 1 N Σ i = 1 N x i 2 − 2 ⋅ μ M L E 2 + μ M L E 2 ~~~~~~~~~~~=\frac{1}{N} \Sigma_{i=1}^{N} x_{i}^{2}-2 \cdot \mu_{M L E}^{2}+\mu_{M L E}^{2} =N1Σi=1Nxi2−2⋅μMLE2+μMLE2
= 1 N Σ i = 1 N x i 2 − μ M L E 2 ~~~~~~~~~~~=\frac{1}{N} \Sigma_{i=1}^{N} x_{i}^{2}-\mu_{M L E}^{2} =N1Σi=1Nxi2−μMLE2
E [ σ M L E 2 ] = E [ 1 N Σ i = 1 N x i 2 − μ M L E 2 ] = E [ ( 1 N Σ i = 1 N x i 2 − μ 2 ) − ( μ M L E 2 − μ 2 ) ] E\left[\sigma_{ML E}^{2}\right]=E\left[\frac{1}{N} \Sigma_{i=1}^{N} x_{i}^{2}-\mu_{M L E}^{2}\right] = E\left[\left(\frac{1}{N} \Sigma_{i=1}^{N} x_{i}^{2}-\mu^{2}\right)-\left(\mu_{M L E}^{2}-\mu^{2}\right)\right] E[σMLE2]=E[N1Σi=1Nxi2−μMLE2]=E[(N1Σi=1Nxi2−μ2)−(μMLE2−μ2)]
= E [ 1 N Σ i = 1 N x i 2 − μ 2 ] − E [ μ M L E 2 − μ 2 ] =E\left[\frac{1}{N} \Sigma_{i=1}^{N} x_{i}^{2}-\mu^{2}\right]-E\left[\mu_{M LE}^{2}-\mu^{2}\right] =E[N1Σi=1Nxi2−μ2]−E[μMLE2−μ2]
E ( 1 N Σ i = 1 N x i 2 − μ 2 ] = E [ 1 N Σ i = 1 N ( x i 2 − μ 2 ) ] E\left(\frac{1}{N} \Sigma_{i=1}^{N} x_{i}^{2}-\mu^{2}\right]=E\left[\frac{1}{N} \Sigma_{i=1}^{N}\left(x_{i}^{2}-\mu^{2}\right)\right] E(N1Σi=1Nxi2−μ2]=E[N1Σi=1N(xi2−μ2)]
= 1 N Σ i = 1 N E ( x i 2 − μ 2 ) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=\frac{1}{N} \Sigma_{i=1}^{N} E\left(x_{i}^{2}-\mu^{2}\right) =N1Σi=1NE(xi2−μ2)
= σ 2 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=\sigma^2 =σ2
E [ μ M L E 2 − μ 2 ] = E [ μ M L E 2 ] − E [ μ 2 ] E\left[\mu_{MLE}^{2}-\mu^{2}\right]=E\left[\mu_{MLE}^{2}\right]-E\left[\mu^{2}\right] E[μMLE2−μ2]=E[μMLE2]−E[μ2]
= E [ μ M L E 2 ] − μ 2 = E [ μ M L E 2 ] − E 2 [ μ M L E ] \begin{array}{l}{~~~~~~~~~~~~~~~~~~~~~~~~~=E\left[\mu_{M L E}^{2}\right]-\mu^{2}} \\ {~~~~~~~~~~~~~~~~~~~~~~~~~=E\left[\mu_{M L E}^{2}\right]-E^{2}\left[\mu_{MLE}\right]}\end{array} =E[μMLE2]−μ2 =E[μMLE2]−E2[μMLE]
= V a r ( μ M L E ) ~~~~~~~~~~~~~~~~~~~~~~~~~~~= Var(\mu_{MLE}) =Var(μMLE)
= var ( 1 N Σ i = 1 N x i ) ~~~~~~~~~~~~~~~~~~~~~~~~~~~= \operatorname{var}\left(\frac{1}{N} \Sigma_{i=1}^{N} x_{i}\right) =var(N1Σi=1Nxi)
= 1 N 2 Σ i = 1 N Var ( x i ) = 1 N 2 Σ i = 1 N σ 2 = 1 N 2 ⋅ N ⋅ σ 2 = 1 N σ 2 \begin{array}{l}{~~~~~~~~~~~~~~~~~~~~~~~~~=\frac{1}{N^{2}} \Sigma_{i=1}^{N} \operatorname{Var}\left(x_{i}\right)=\frac{1}{N^{2}} \Sigma_{i=1}^{N} \sigma^{2}} \\ {~~~~~~~~~~~~~~~~~~~~~~~~~=\frac{1}{N^{2}} \cdot N \cdot \sigma^{2}=\frac{1}{N} \sigma^{2}}\end{array} =N21Σi=1NVar(xi)=N21Σi=1Nσ2 =N21⋅N⋅σ2=N1σ2
最终得到
E [ σ M L E 2 ] = σ 2 − 1 N σ 2 = N − 1 N σ 2 ≠ σ 2 E\left[\sigma_{MLE}^{2}\right]=\sigma^{2}-\frac{1}{N} \sigma^{2}=\frac{N-1}{N} \sigma^{2} \neq \sigma^2 E[σMLE2]=σ2−N1σ2=NN−1σ2̸=σ2 (有偏估计)
容易得出利用最大似然估计法估计高斯分布的方差会偏小!!!
极大似然估计针对于高斯分布的方差估计会造成一定的偏差。
实际上其方差的无偏估计为:
σ ^ 2 = 1 N − 1 Σ i = 1 N ( x i − μ M L E 2 ) \hat{\sigma}^{2}=\frac{1}{N-1} \Sigma_{i=1}^{N}\left(x_{i}-\mu_{M L E}^{2}\right) σ^2=N−11Σi=1N(xi−μMLE2)
二维高斯分布的可视化探究
多维高斯分布: x ∼ p ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 exp ( − 1 2 ( x − μ ) ⊤ Σ − 1 ( x − μ ) ) x \sim p(x)=\frac{1}{(2 \pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left(-\frac{1}{2}(x-\mu)^{\top} \Sigma^{-1}(x-\mu)\right) x∼p(x)=(2π)2n∣Σ∣211exp(−21(x−μ)⊤Σ−1(x−μ))
x ∈ R p , x \in \mathbb{R}^{p}, x∈Rp, p 维的随机向量。
x = ( x 1 x 2 ⋮ x p ) , x=\left(\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{p}}\end{array}\right), x=⎝⎜⎜⎜⎛x1x2⋮xp⎠⎟⎟⎟⎞, μ = ( μ 1 μ 2 ⋮ μ p ) \mu=\left(\begin{array}{c}{\mu_{1}} \\ {\mu_{2}} \\ {\vdots} \\ {\mu_{p}}\end{array}\right) μ=⎝⎜⎜⎜⎛μ1μ2⋮μp⎠⎟⎟⎟⎞, Σ = ( σ 11 σ 12 … σ 1 p σ 21 σ 22 … σ 2 p ⋮ ⋮ ⋱ ⋮ σ P 1 σ p 2 ⋯ σ p p ) \Sigma=\left(\begin{array}{ccc}{\sigma_{11}} & {\sigma_{12}} & {\dots}& {\sigma_{1p}} \\ {\sigma_{21}} & {\sigma_{22}} & {\dots}& {\sigma_{2p}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots}\\ {\sigma_{P 1}} & {\sigma_{p 2}} & {\cdots}& {\sigma_{pp}}\end{array}\right) Σ=⎝⎜⎜⎜⎛σ11σ21⋮σP1σ12σ22⋮σp2……⋱⋯σ1pσ2p⋮σpp⎠⎟⎟⎟⎞, 假设 Σ ~\Sigma~ Σ 为正定的(一般情况下为半正定)
( x − μ ) T Σ − 1 ( x − μ ) (x-\mu)^{T} \Sigma^{-1}(x-\mu) (x−μ)TΣ−1(x−μ)(二次型), 马氏距离
Σ = 1 \Sigma = 1 Σ=1, 马氏距离为欧氏距离。
Σ \Sigma~ Σ 的相似对角化(特征分解)
Σ = u ∧ u ⊤ , u u ⊤ = u ⊤ u = I \Sigma=u \wedge u^{\top}, u u^{\top}=u^{\top} u=I Σ=u∧u⊤,uu⊤=u⊤u=I(正交)
∧ = diag ( λ i ) , i = 1 , ⋯ , p ⋅ , λ i ∈ C \wedge=\operatorname{diag}\left(\lambda_{i}\right), i=1, \cdots, p_{\cdot}, \lambda_{i} \in C ∧=diag(λi),i=1,⋯,p⋅,λi∈C
U = ( u 1 , ⋯ , u p ) p × p U=\left(u_{1}, \cdots, u_{p}\right)_{p \times p} U=(u1,⋯,up)p×p
Σ = u ∧ u ⊤ = ( u 1 , … u p ) ( λ 1 ⋱ λ p ) ( u 1 ⊤ ⋮ u p ⊤ ) \Sigma=u \wedge u^{\top}=\left(u_{1}, \ldots u_{p}\right)\left(\begin{array}{ccc}{\lambda_{1}} \\ {} & {\ddots} & {} \\ {} & {} & {\lambda_{p}}\end{array}\right)\left(\begin{array}{c}{u_{1}^{\top}} \\ {\vdots} \\ {u_{p}^{\top}}\end{array}\right) Σ=u∧u⊤=(u1,…up)⎝⎛λ1⋱λp⎠⎞⎝⎜⎛u1⊤⋮up⊤⎠⎟⎞
= ( u 1 λ 1 ⋯ u p λ p ) ( u 1 ⊤ ⋮ u p ⊤ ) ~~~~=\left(u_{1} \lambda_{1} \cdots u_{p} \lambda_{p}\right)\left(\begin{array}{l}{u_{1}^{\top}} \\ \vdots \\ {u_{p}^{\top}}\end{array}\right) =(u1λ1⋯upλp)⎝⎜⎛u1⊤⋮up⊤⎠⎟⎞ = Σ i = 1 p u i λ i u i ⊤ =\Sigma_{i=1}^{p} u_{i} \lambda_{i} u_{i}^{\top} =Σi=1puiλiui⊤
Σ − 1 = ( u ∧ u ⊤ ) − 1 = ( u T ) − 1 ∧ − 1 u − 1 = u Λ − 1 u T = Σ i = 1 p u i 1 λ i u i T \Sigma^{-1}=\left(u \wedge u^{\top}\right)^{-1}=\left(u^{T}\right)^{-1} \wedge^{-1} u^{-1}=u \Lambda^{-1} u^{T}=\Sigma_{i=1}^{p} u_{i} \frac{1}{\lambda i} u_{i}^{T} Σ−1=(u∧u⊤)−1=(uT)−1∧−1u−1=uΛ−1uT=Σi=1puiλi1uiT
∧ − 1 = diag ( 1 λ i ) , i = 1 , ⋯ , p \wedge^{-1}=\operatorname{diag}\left(\frac{1}{\lambda_{i}}\right), i=1, \cdots, p ∧−1=diag(λi1),i=1,⋯,p
Δ = ( x − μ ) Σ − 1 ∣ x − μ ) = ( x − μ ) ⊤ Σ i = 1 p u i 1 λ i ⋅ u i ⊤ ( x − μ ) = Σ i = 1 p ( x − μ ) ⊤ u 1 1 λ i u i ⊤ ( x − μ ) 令 y = ( y 1 ⋮ y p ) = ( x − μ ) ⊤ u i = Σ i = 1 p y i 1 λ i y i T = Σ i = 1 p y i 2 λ i \begin{aligned} \Delta=(x-\mu) \Sigma^{-1} | x-\mu ) &=(x-\mu)^{\top} \Sigma_{i=1}^{p} u_{i} \frac{1}{\lambda i} \cdot u_{i}^{\top}(x-\mu) \\ &=\Sigma_{i=1}^{p}(x-\mu)^{\top} u_{1} \frac{1}{\lambda_{i}} u_{i}^{\top}(x-\mu)\\ &令 ~y=\left(\begin{array}{l}{y_{1}} \\ {\vdots} \\ {y_{p}}\end{array}\right)=(x-\mu)^{\top} u_{i}\\& =\Sigma_{i=1}^{p} y_{i} \frac{1}{\lambda_{i}} y_{i}^{T}=\Sigma_{i=1}^{p} \frac{y_{i}^{2}}{\lambda_{i}} \end{aligned} Δ=(x−μ)Σ−1∣x−μ)=(x−μ)⊤Σi=1puiλi1⋅ui⊤(x−μ)=Σi=1p(x−μ)⊤u1λi1ui⊤(x−μ)令 y=⎝⎜⎛y1⋮yp⎠⎟⎞=(x−μ)⊤ui=Σi=1pyiλi1yiT=Σi=1pλiyi2
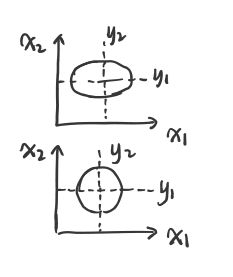
令 p = 2, Δ = y 1 2 λ 1 + y 2 2 λ 2 = 1 ( λ 1 > λ 2 ) \Delta=\frac{y_{1}^{2}}{\lambda_{1}}+\frac{y_{2}^{2}}{\lambda_{2}}=1(\lambda_1>\lambda_2) Δ=λ1y12+λ2y22=1(λ1>λ2)
总结:
令 Δ = ( x − μ ) T Σ − 1 ( x − μ ) \Delta=(x-\mu)^{T} \Sigma^{-1}(x-\mu) Δ=(x−μ)TΣ−1(x−μ)
p ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 exp ( − 1 2 Δ ) p(x)=\frac{1}{(2 \pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left(-\frac{1}{2} \Delta\right) p(x)=(2π)2n∣Σ∣211exp(−21Δ)
令 p = 0.5 → Δ = r 1 p=0.5 \rightarrow \Delta=r_{1} p=0.5→Δ=r1, 对应一个 y 1 2 λ 1 + y 2 2 λ 2 = r 1 \frac{y_{1}^{2}}{\lambda_{1}}+\frac{y_{2}^{2}}{\lambda_{2}}=r_{1} λ1y12+λ2y22=r1 椭圆。
令 p = 0.6 → Δ = r 2 p=0.6 \rightarrow \Delta=r_{2} p=0.6→Δ=r2, 对应一个 y 1 2 λ 1 + y 2 2 λ 2 = r 2 \frac{y_{1}^{2}}{\lambda_{1}}+\frac{y_{2}^{2}}{\lambda_{2}}=r_{2} λ1y12+λ2y22=r2 椭圆。
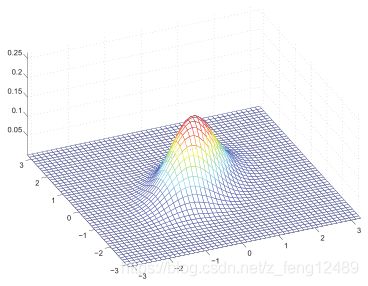
当 μ = [ 0 , 0 ] T , Σ = [ 1 0.5 0.5 1 ] \mu = [0, 0]^T, \Sigma = \left[\begin{array}{cc}{1} & {0.5} \\ {0.5} & {1}\end{array}\right] μ=[0,0]T,Σ=[10.50.51] 如图所示。
高斯分布的局限性
局限一: 参数过大时,难以快速学习
Σ P × P → P 2 − P 2 + p = p 2 + P 2 \Sigma_{P \times P} \rightarrow \frac{P^{2}-P}{2}+p=\frac{p^{2}+P}{2}~~~~~~ ΣP×P→2P2−P+p=2p2+P 参数个数 O ( p 2 ) O(p^2)~~~~~~~~~~~~ O(p2) 参数过大 学习困难
-
假设 Σ p × p \Sigma_{p \times p}~ Σp×p 方差矩阵为对角矩阵, ( λ 1 ⋱ λ p ) \left(\begin{array}{ccc}{\lambda_{1}} \\ {} & {\ddots} & {} \\ {} & {} & {\lambda_{p}}\end{array}\right) ⎝⎛λ1⋱λp⎠⎞ 来缩小参数。
-
假设 Σ p × p \Sigma_{p \times p}~ Σp×p 方差矩阵为对角矩阵,且 λ 1 = λ 2 = . . . = λ p = λ \lambda_1=\lambda_2=...=\lambda_p=\lambda~~~~~ λ1=λ2=...=λp=λ 即就是 ( λ ⋱ λ ) \left(\begin{array}{ccc}{\lambda_{}} \\ {} & {\ddots} & {} \\ {} & {} & {\lambda_{}}\end{array}\right) ⎝⎛λ⋱λ⎠⎞ 来进一步缩小参数。
factor analysis 假设为 对角矩阵。
P-PCA 各向同性。
局限二: 有些时候用一个高斯分布建模难以确切表达模型。
GMM (高斯混合模型)采用多个高斯分布建模。
求多维高斯分布的边缘分布和条件概率分布
已知高维高斯分布的随机变量,均值,协方差:
~
x = ( x 1 x 2 ⋮ x p ) μ = ( μ 1 μ 2 ⋮ μ p ) Σ = ( σ 11 σ 12 ⋯ σ 1 p σ 21 σ 22 ⋯ σ 2 p ⋮ ⋮ ⋱ ⋮ σ p 1 σ p 2 ⋯ σ p p ) p × p x=\left(\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{p}}\end{array}\right) \quad \mu=\left(\begin{array}{c}{\mu_{1}} \\ {\mu_{2}} \\ {\vdots} \\ {\mu_{p}}\end{array}\right)~~\Sigma=\left(\begin{array}{cccc}{\sigma_{11}} & {\sigma_{12}} & {\cdots} & {\sigma_{1 p}} \\ {\sigma_{21}} & {\sigma_{22}} & {\cdots} & {\sigma_{2 p}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\sigma_{p 1}} & {\sigma_{p 2}} & {\cdots} & {\sigma_{p p}}\end{array}\right)_{p \times p} x=⎝⎜⎜⎜⎛x1x2⋮xp⎠⎟⎟⎟⎞μ=⎝⎜⎜⎜⎛μ1μ2⋮μp⎠⎟⎟⎟⎞ Σ=⎝⎜⎜⎜⎛σ11σ21⋮σp1σ12σ22⋮σp2⋯⋯⋱⋯σ1pσ2p⋮σpp⎠⎟⎟⎟⎞p×p
~
由于要求条件概率以及边缘概率,将随机变量分成两组:
~
x = ( x a x b ) ( m ) ( n ) m + n = p μ = ( μ a μ b ) Σ = ( Σ a a Σ a b Σ b a Σ b b ) x=\left(\begin{array}{l}{x_{a}} \\ {x_{b}}\end{array}\right) \begin{array}{l}{(m)} \\ {(n)}\end{array} \quad m+n=p \quad \mu=\left(\begin{array}{l}{\mu_{a}} \\ {\mu_{b}}\end{array}\right)~~\Sigma=\left(\begin{array}{ll}{\Sigma_{a a}} & {\Sigma_{a b}} \\ {\Sigma_{b a}} & {{\Sigma}_{b b}}\end{array}\right) x=(xaxb)(m)(n)m+n=pμ=(μaμb) Σ=(ΣaaΣbaΣabΣbb)
~
求: P ( x a ) , P ( x b ∣ x a ) , P ( x b ) , P ( x a ∣ x b ) P\left(x_{a}\right), P\left(x_{b} | x_{a}\right), P\left(x_{b}\right), P\left(x_{a} | x_{b}\right) P(xa),P(xb∣xa),P(xb),P(xa∣xb)
在 PRML 中通用方法是配方法,思想简单,但计算量大。这里不使用。
引入定理: x ∼ N ( μ , Σ ) , y = A x + B , x \sim N(\mu, \Sigma), y=Ax+B, x∼N(μ,Σ),y=Ax+B, 则 y ∼ N ( A μ + B , A Σ A ⊤ ) y \sim N\left(A \mu+B, A \Sigma A^{\top}\right) y∼N(Aμ+B,AΣA⊤)
~
E [ y ] = E [ A x + B ] = A E [ x ] + B = A μ + B E[y]=E[A x+B]=A E[x]+B=A \mu+B E[y]=E[Ax+B]=AE[x]+B=Aμ+B
var [ y ] = var [ A x + B ] = var [ A x ] + var ( B ] = A var [ x ] A T = A Σ A T \operatorname{var}[y]=\operatorname{var}[A x+B]=\operatorname{var}[A x]+\operatorname{var}(B]=A \operatorname{var}[x] A^{T}=A \Sigma A^{T} var[y]=var[Ax+B]=var[Ax]+var(B]=Avar[x]AT=AΣAT
解:
构造: x a = A x = ( I m 0 ) ( x a x b ) = x a x_{a}=Ax=\left(I_{m}~~ 0\right)\left(\begin{array}{l}{x_{a}} \\ {x_{b}}\end{array}\right)=x_a xa=Ax=(Im 0)(xaxb)=xa
有上述定理得:
E [ x a ] = ( I m 0 ) ( μ a μ b ) = μ a E\left[x_{a}\right]=\left(I_{m} 0\right)\left(\begin{array}{l}{\mu_{a}} \\ {\mu_{b}}\end{array}\right)=\mu_{a} E[xa]=(Im0)(μaμb)=μa
var [ y ] = var [ A x + B ] = var [ A x ] + var [ B ] = A Var [ x ] A T = A Σ A T \operatorname{var}[y]=\operatorname{var}[A x+B]=\operatorname{var}[A x]+\operatorname{var}[B]=A \operatorname{Var}[x] A^{T}=A \Sigma A^{T} var[y]=var[Ax+B]=var[Ax]+var[B]=AVar[x]AT=AΣAT
所以: x a ∼ N ( μ a , Σ a a ) x_{a} \sim N\left(\mu_{a}, \Sigma_{a a}\right) xa∼N(μa,Σaa)
~
求 x b ∣ x a ~x_b|x_a xb∣xa
~~~
定义三个变量:
x b ⋅ a = x b − Σ b a Σ a a − 1 x a μ b ⋅ a = μ b − Σ b a Σ a a − 1 μ a Σ b b ⋅ a = Σ b b − Σ b a Σ a a − 1 Σ a b \begin{array}{l}{x_{b \cdot a}=x_{b}-\Sigma_{b a} \Sigma_{a a}^{-1} x_{a}} \\ {\mu_{b \cdot a}=\mu_{b}-\Sigma_{b a} \Sigma_{a a}^{-1} \mu_{a}} \\ {\Sigma_{b b\cdot a}=\Sigma_{b b}-\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a b}}\end{array} xb⋅a=xb−ΣbaΣaa−1xaμb⋅a=μb−ΣbaΣaa−1μaΣbb⋅a=Σbb−ΣbaΣaa−1Σab
~
~~ 其中 Σ b b ⋅ a ~\Sigma_{b b\cdot a} Σbb⋅a 称为 schur complementary. (线性代数)
~
那么易构造 x b ⋅ a = ( − Σ b a Σ a a − 1 I n ) ( x a x b ) x_{b \cdot a}=\left(-\Sigma_{b a} \Sigma_{a a}^{-1} ~I_{n}\right)\left(\begin{array}{l}{x_{a}} \\ {x_{b}}\end{array}\right) xb⋅a=(−ΣbaΣaa−1 In)(xaxb)
由上述定理得:
E [ x b ⋅ a ] = ( − Σ b a Σ a a − 1 I n ) ( μ a μ b ) = μ b − Σ b a Σ a a − 1 μ a = μ b ⋅ a E\left[x_{b\cdot a}\right]=\left(-\Sigma_{b a} \Sigma_{a a}^{-1} I_{n}\right)\left(\begin{array}{l}{\mu_{a}} \\ {\mu_{b}}\end{array}\right)=\mu_{b}-\Sigma_{b a} \Sigma_{a a}^{-1} \mu_{a}=\mu_{b\cdot a} E[xb⋅a]=(−ΣbaΣaa−1In)(μaμb)=μb−ΣbaΣaa−1μa=μb⋅a
var [ x b ⋅ a ] = ( − Σ b a Σ a a − 1 I n ) ( Σ a a − 1 Σ a b Σ b a Σ b b ) ( − Σ a a − 1 Σ b a T I n ) \operatorname{var}\left[x_{b \cdot a}\right]=\left(-\Sigma_{b a} \Sigma_{a a}^{-1} I_{n}\right)\left(\begin{array}{l}{\Sigma_{a a} ^{-1}\Sigma_{a b}} \\ {\Sigma_{b a} \Sigma_{b b}}\end{array}\right)\left(\begin{array}{c}{-\Sigma_{a a}^{-1} \Sigma_{b a}^T} \\ {I_{n}}\end{array}\right) var[xb⋅a]=(−ΣbaΣaa−1In)(Σaa−1ΣabΣbaΣbb)(−Σaa−1ΣbaTIn)
= = ( 0 ⋅ Σ b b − Σ b a Σ a a − 1 Σ a b ) ( − Σ a a − 1 Σ b a T I n ) = Σ b b − Σ b a Σ a a − 1 Σ a b = Σ b b ⋅ a ~~~~~~~~~~~~~~~==\left(0 \cdot \Sigma_{b b}-\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a b}\right)\left(\begin{array}{c}{-\Sigma_{a a}^{-1} \Sigma_{b a}^T} \\ {I_{n}}\end{array}\right)=\Sigma_{b b}-\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a b}=\Sigma_{b b\cdot a} ==(0⋅Σbb−ΣbaΣaa−1Σab)(−Σaa−1ΣbaTIn)=Σbb−ΣbaΣaa−1Σab=Σbb⋅a
x b ⋅ a ∼ N ( μ b ⋅ a , Σ b b ⋅ a ) x_{b\cdot a} \sim N\left(\mu_{b\cdot a}, \Sigma_{b b\cdot a}\right) xb⋅a∼N(μb⋅a,Σbb⋅a)
x b ⋅ a = x b − Σ b a Σ a a − 1 x a ⇒ x b = x b a + Σ b a Σ a a − 1 x a x_{b\cdot a}=x_{b}-\Sigma_{b a} \Sigma_{a a}^{-1} x_{a} \Rightarrow x_{b}=x_{b a}+\Sigma_{b a} \Sigma_{a a}^{-1} x_{a}~~~ xb⋅a=xb−ΣbaΣaa−1xa⇒xb=xba+ΣbaΣaa−1xa 这里 x a x_a xa为常数。
~
E [ x b ∣ x a ] = μ b ⋅ a + ∑ b a ∑ a a − 1 x a var [ x b ∣ x a ] = var [ x b ⋅ a ] = ∑ b b ⋅ a \begin{array}{l}{E\left[x_{b} | x_{a}\right]=\mu_{b \cdot a}+\sum_{b a} \sum_{a a}^{-1} x_{a}} \\ {\operatorname{var}\left[x_{b} | x_{a}\right]=\operatorname{var}\left[x_{b \cdot a}\right]=\sum_{b b \cdot a}}\end{array} E[xb∣xa]=μb⋅a+∑ba∑aa−1xavar[xb∣xa]=var[xb⋅a]=∑bb⋅a
~
x b ∣ x a ∼ N ( μ b a + Σ b ⋅ a Σ a a − 1 x a , Σ b b ⋅ a ) x_{b} | x_{a} \sim N\left(\mu_{b a}+\Sigma_{b\cdot a}{\Sigma}_{a a}^{-1} x_{a}, \Sigma_{b b\cdot a}\right) xb∣xa∼N(μba+Σb⋅aΣaa−1xa,Σbb⋅a)