题目练习：万金油DFS

 

之前也刷了一些题目，但是效果不是很好，看到题目也不能马上想到是用什么方法做，反思了下应该是做的题目太散了，一天做链表，第二天又做图，这样导致每个结构都不是特别熟悉。所以接下来刷题会按照Tag刷，今天就刷万金油的DFS.

应该说DFS能够解决特别多的问题，因为每一种可能都能遍历到，可以用来解决排列，组合，幂集、子集、0-1 背包、n 括号问题、八皇后、迷宫、…当然这些问题有些能通过动态规划来解，比如迷宫类的问题输入棋盘型DP，而0-1背包本身就属于一类问题了。

1.全排列问题 

3.子集问题

6.数组总和问题

8.字符串排列

9.有效括号

.

第一题：

全排列问题 https://leetcode-cn.com/problems/permutations/

问题描述：

 给定一个没有重复数字的序列，返回其所有可能的全排列。

class Solution {
public:
    vector> result;
    vector path;
    vector> permute(vector& nums) {

        if(nums.size() == 0) return result;
        vector visit(nums.size(),false);
        dfs(nums,visit);
        return result; 
    }
    void dfs(vector& nums,vector&visit){
        if(path.size() == nums.size()){
            result.push_back(path);
            return;
        }
        for(int i = 0 ; i < nums.size(); i++){
            if(!visit[i]){
                path.push_back(nums[i]);//当前的选择
                visit[i] = true;
                dfs(nums,visit);
                path.pop_back();
                visit[i] = false;       //撤销当前选择
        }
        }   
    }
};

总结:自己写这个代码的时候把所有的东西都当作形参传递了，可能会引起stackoverflow，所以还是参考上面这个把。

 

第二题：

全排列问题II

搜索去重，错误的想法是先找出所有答案，然后去重，如[1 1 1 1 1 ]，如果按照全部搜索的话，那么会有2^6次，而答案只有7种

 

 

 

第三题：

子集 问题  https://leetcode-cn.com/problems/subsets/

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

class Solution {
public:

    vector> result;
    vector path;
    vector> subsets(vector& nums) {
        vector visit(nums.size(),false);
        if(nums.size()==0) return result;
        sort(nums.begin(),nums.end());
        dfs(nums,0);
        return result;
    }
    void dfs(vector& nums,int startIndex){
        //与全排列的区别是不需要判断是否达到终点也可以，因为进不到for循环里面
        result.push_back(path);
        
        //子集中唯一不同的就是不需要标志当前数已经被访问过了，因为我们每次访问staetIndex都会+1的，所以不存在这样的问题
        for(int i = startIndex ; i < nums.size(); i++){
                path.push_back(nums[i]);
        
                dfs(nums,i+1);//一开始这里写成startIndex+1,调试了好久....

                path.pop_back();
            }         
        }
};

第四题：

全子集II待续

 

第五题：电话号码的组合 https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

 

class Solution {
public:
    vector results;
    string subset;
    const vector keyboard = {"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    vector letterCombinations(string digits) {
        if(digits.size()==0) return results;
        dfs(digits,0);
        return results;
    }
    void dfs(string& digits,int curLevel){
        if(subset.size() == digits.size()){
            results.push_back(subset);
            return;
        }

            for(auto it : keyboard[digits[curLevel]- '2']){
                subset = subset + it; //从选择列表中选一个
                dfs(digits,curLevel+1);
                subset.erase(subset.end()-1);//从选择列表中删除
            }
        }  
};

可以看出不管是子集还是号码组合DFS中都需要+1，因为数字不断得往前推进。

 

 

第六题：组合总和 https://leetcode-cn.com/problems/combination-sum/submissions/

给定一个候选数字的集合 candidates 和一个目标值 target. 找到 candidates 中所有的和为 target 的组合.

在同一个组合中, candidates 中的某个数字不限次数地出现.

1. 所有数值 (包括 target ) 都是正整数.
2. 返回的每一个组合内的数字必须是非降序的.
3. 返回的所有组合之间可以是任意顺序.
4. 解集不能包含重复的组合.

输入: candidates = [2, 3, 6, 7], target = 7
输出: [[7], [2, 2, 3]]

第一次看以为是无限背包问题，然后发现还真的是，不过背包问题只能求出方案数...下面为

第七题：

给出 n 个物品, 以及一个数组, nums[i]代表第i个物品的大小, 保证大小均为正数并且没有重复, 正整数 target 表示背包的大小, 找到能填满背包的方案数。
每一个物品可以使用无数次

输入: nums = [2,3,6,7] 和 target = 7
输出: 2
解释:
方案有: 
[7]
[2, 2, 3]

class Solution {
public:
    vector> result;
    vector path;
    int CurSum;
    vector> combinationSum(vector& candidates, int target) {
        if(candidates.size() == 0) return result;
        sort(candidates.begin(),candidates.end());//这里需要先进行排序下
        dfs(candidates,target,candidates[0]);
        return result;
    }
    void dfs(vector& candidates,int target,int lastNum){
        if(CurSum >= target){
            if(CurSum == target) result.push_back(path);
            return;
        }

        for(int i = 0 ; i < candidates.size(); i++){
            if(candidates[i] < lastNum){//当前数必须大于等于上一个数，这也也就是说前
                continue;
            }

            CurSum += candidates[i];
            path.push_back(candidates[i]);

            dfs(candidates,target,candidates[i]);

            CurSum -= candidates[i];
            path.pop_back();
        }

    }
};

其题搜索树如下：

 

题目8：

字符串的排列

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

一种做法是直接用set进行去重操作，不过那种效率太慢了

class Solution {
public:
    set result;
    string path;
    
    vector permutation(string s) {
        if(s.size() == 0 ) return vector();
        vector visit(s.size()+1,false);
        dfs(s,visit);
        return vector(result.begin(), result.end());
    }
    void dfs(string& s,vector& visit){
        if(path.size() == s.size()){
            result.insert(path);
            return;
        }

        for(int i = 0 ; i < s.size(); i++){
            if(!visit[i]){
                 visit[i] = true;
                 path =  path + s[i];
                 dfs(s,visit);
                 visit[i] = false;
                 path.erase(path.end()-1);
            }
          
        }
    }

};

class Solution {
public:
    vector result;
    string path;
    
    vector permutation(string s) {
        if(s.size() == 0 ) return vector();
        sort(s.begin(),s.end());
        vector visit(s.size()+1,false);
        dfs(s,visit);
        return result;
    }
    void dfs(string& s,vector& visit){
        if(path.size() == s.size()){
            result.push_back(path);
            return;
        }

        for(int i = 0 ; i < s.size(); i++){
            

            if(visit[i]) continue;
            //如果上一个没有被访问到就访问到了下一个,那么就跳过
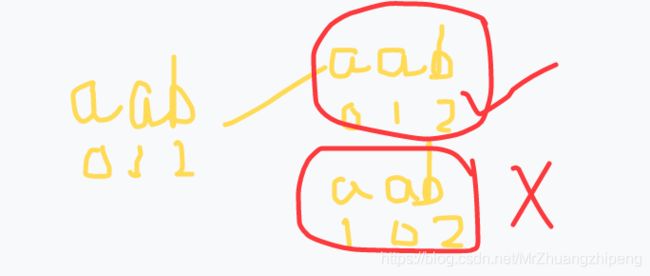
            if(i>0 && s[i-1]==s[i] && !visit[i-1]) continue;

                 visit[i] = true;
                 path =  path + s[i];
                 dfs(s,visit);
                 visit[i] = false;
                 path.erase(path.end()-1);
            
          
        }
    }

};

 

 

题目9：给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

class Solution {
public:
    vector result;
    string subset;
    vector generateParenthesis(int n) {
        char s[2] = {'(',')'};
        dfs(n,s);
        return result;
    }
    void dfs(int n,const char* s){
        if(subset.size()==n*2){
            if(checkValid(subset)){
                result.push_back(subset);
            }
            return;
        }

        for(int i =  0; i < 2; i++){
            subset = subset + s[i];
            if(Continue(subset)){
                dfs(n,s);
            }          
            subset.erase(subset.end()-1);
        }

    }
    //为了在递归的时候减枝
    bool Continue(const string& str){
        int count = 0;
        for(int i = 0 ; i < str.size();i++){
            if(str[i] == '(') count++;
            else              count--;
            if(count < 0) return false;
        }
        return true;
    }
    //为了在结果的时候找出正确的元素
    bool checkValid(const string& str){
        int count = 0;
        for(int i = 0 ; i < str.size();i++){
            if(str[i] == '(') count++;
            else              count--;

            if(count < 0) return false;
        }
        if(count == 0)
             return true;
        return false;
    }
};

上面的结果实际上没有涉及太多的减枝过程，后面参考了leetcode某位神的做法

class Solution {
public:
    vector result;
    string subset;
    vector generateParenthesis(int n) {
        dfs(0,0,n);
        return result;
    }
    void dfs(int left,int right,int n){
        if(left == n && right ==n){
            result.push_back(subset);
            return;
        }
        if(left < right)
            return;
    
        if(left < n){
                        
            subset = subset + '(';
            dfs(left+1,right,n);
            subset.erase(subset.end()-1);
        }

        if(right < n){
            subset = subset + ')';
            dfs(left,right+1,n);
            subset.erase(subset.end()-1);     
        }
    }
 
};

 

 

总结:用回溯做的题目套路都差不多，一个模板就是

class Solution {
public:
    result;
    subset;

    void dfs(xxx){
       
            if(满足条件){
                result.push_back(subset);
                return;
            }
           
            if(满足条件) {
                做一些减枝操作  
            }

        for(xxx){
            subset = subset + s[i];            
            dfs(n,s);               
            subset.erase(subset.end()-1);
        }

    }

主要比较麻烦的就是处理重复的时候，比较经典的去重方法，就是字符串这个操作

  if(i>0 && s[i-1]==s[i] && !visit[i-1]) continue;

 

后面有时间再补补其他题目..