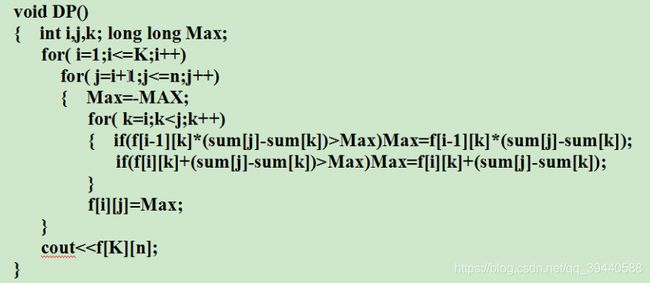bsoj 1035 -- 【练习题目】最大的算式

1035 -- 【练习题目】最大的算式

Description

　　题目很简单，给出N个数字，不改变它们的相对位置，在中间加入K个乘号和N-K-1个加号，（括号随便加）使最终结果尽量大。因为乘号和加号一共就是N-1个了，所以恰好每两个相邻数字之间都有一个符号。例如：
　　N=5，K=2，5个数字分别为1、2、3、4、5，可以加成：
　　　　1*2*(3+4+5)=24
　　　　1*(2+3)*(4+5)=45
　　　　(1*2+3)*(4+5)=45
　　　　……

Input

　　输入文件共有二行。
　　第一行为两个有空格隔开的整数，表示N和K，其中（2<=N<=15, 0<=K<=N-1）。
　　第二行为 N个用空格隔开的数字（每个数字在0到9之间）。

Output

　　输出文件仅一行包含一个整数，表示要求的最大的结果

Sample Input

5 2 1 2 3 4 5

Sample Output

120

Hint

【样例说明】(1+2+3)*4*5=120

题解如下：

我的心路历程：

刚开始我想的是石子合并
然后辛辛苦苦打完发现样例过不了
开始怀疑人生
然后去看了看别人写的
发现都用的资源分配！！
然后我就删掉了我的石子合并
结果90分发现资源分配是错的！！
此时我已经删掉了我的石子合并！！！
然后开启今日份的快乐找代码
终于恢复了我自己的石子合并。。。。
（还好恢复了）

so为什么大多数资源分配不对呢？

请看下面一组样例：
5 3
1 1 0 0 0
正确的分发应该是

（1*1）+（0*0*0）=1

可见在这组数据中，真正把1和0两部分区分开的是+号（因为加号比较少嘛）

所以对于这组样例，网上大多数资源分配类做的就不对了，因为我们分的不只有乘号还有加号对不对？

我们先来回顾一下资源分配和石子合并

资源分配是站在我现在看过去然后把过去某一节点之前分成一段，这个节点之后分成另一段，

而合并是站在中间，左牵黄，右擎苍，左边抱一个，右边抱一个。

正因为不只有乘号还有加号，就不应该只是分配（你见过分配两个东西的资源分配嘛？没有！）

所以是石子合并。

但是某一种神奇的资源分配没有问题（如果你同时考虑了加号和乘号）

但是我有这个闲心还不如来写石子合并比较安全

资源分配如下：

 

so我们怎么合并呢？

先康康这道题有哪些变量：

石子合并肯定有from和to（简称i和j），便是两维，而我们还要限制乘号的个数呐！所以就还有w限制乘号的个数

（石子合并最基本的用t来枚举状态作为i~j的长度我想我应该不用说了）

于是诞生了f[i,j,w]

case1.f[i][j][w]=max(f[i][j][w],f[i][k][p]+f[k+1][j][w-p]);（用加号当中间人）

case2.f[i][j][w]=max(f[i][j][w],f[i][k][p]*f[k+1][j][w-p-1]);（乘号）

其中：t∈(1,n]，i∈[1,n-t]，j∈[i,j]，p∈[0,w]

即为：用w个乘号合并i~k与k+1~j的数，以形成i~j这一段的最大值，其中，i~k这一段用去p个乘号，如果是case2，就还要多用去一个乘号，即后面半段是w-p-1个乘号。

然后你就高高兴兴的拿着类似于下面的代码去提交。。。。

//在来日终可期的宿命中，你是蝴蝶振翅后注定的重逢与相守。
//——许墨
#include
#include
#define ll long long
#define inf 1e9
#define love_xumoforever main
using namespace std;
ll f[20][20][20];
int a[20];
int love_Xumo_forever() {
	int n,m,i,j,w,k,p;
	ll ans=0;
	scanf("%d%d",&n,&m);
	for(i=1; i<=n; i++) scanf("%d",&a[i]);
	for(i=1; i<=n; i++) f[i][i][0]=a[i];
	for(int t=1; t

guess what? 在某一个名为bsoj的网站上，只有80分（或者90分）

当然80分是因为long long，而90分，你会发现连

5 3
1 1 0 0 0

都过不了！

“你是不是骗我，这个和资源分配有什么区别？代码又臭又长”

so坑点再次出现：

想想当年石子合并，和现在唯一的区别？

原来没有限制w（乘号个数）是吧。。。。就2维高高兴兴搞定。。。。

so。。。。。。。

You see，如果乘号不合法怎么办？？

于是：

case1.

         if(k-i>=p&&j-k-1>=w-p) f[i][j][w]=max(f[i][j][w],f[i][k][p]+f[k+1][j][w-p]);

        （用加号当中间人）

case2.

          if(k-i>=p&&j-k>=w-p) f[i][j][w]=max(f[i][j][w],f[i][k][p]*f[k+1][j][w-p-1]);

         （乘号）

这个意思就是：前面的乘号个数必须小于前面的数-1，后面同理

大功告成！！

上最终代码：

//在来日终可期的宿命中，你是蝴蝶振翅后注定的重逢与相守。
//——许墨
#include
#include
#define ll long long
#define inf 1e9
#define love_xumoforever main
using namespace std;
ll f[20][20][20];
int a[20];
int love_Xumo_forever() {
	int n,m,i,j,w,k,p;
	ll ans=0;
	scanf("%d%d",&n,&m);
	for(i=1; i<=n; i++) scanf("%d",&a[i]);
	for(i=1; i<=n; i++) f[i][i][0]=a[i];
	for(int t=1; t=p&&j-k-1>=w-p)
							f[i][j][w]=max(f[i][j][w],f[i][k][p]+f[k+1][j][w-p]);
						if(k-i>=p&&j-k>=w-p)
							f[i][j][w]=max(f[i][j][w],f[i][k][p]*f[k+1][j][w-p-1]);
					}
				if(w==m) ans=max(ans,f[i][j][w]);
			}
		}
	printf("%lld\n",ans);
	return 0;
}