全方位分析动态规划的01背包问题，看完还不懂算我输！

最近年级会出了个NEUCDN活动，为了所谓的德育分 提高自己攥写博客的能力就来写一篇博客吧，至于为什么写的是01背包问题呢~啊哈，你以为我会告诉你是因为刚好算法分析与设计这门课要我们小组汇报的是DP之01背包问题…吗？

啊！西马塔！不小心说漏漏嘴了哦豁~

动态规划定义/特点/实现方式

直接进入正题：
首先按照国际惯例走个流程来下一个定义关于什么是动态规划：
（当然摘选自wiki百科了，某度不能信（不是））
动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。（如果你学经济学的话貌似运筹学那一块会介绍到相关的内容）

动态规划的实现分为两种，有递归和迭代。递归一般是自顶向下，依赖于子问题优化函数的结果，只有子问题完全求出，也就是子问题的递归返回结果，原问题才能求解。迭代法，就是巧妙的安排求解顺序，从最小的子问题开始，自下而上求解。每次求新的问题时，子问题的解已经计算出来了。

先说一下自己对于DP的一个理解啊准不准确另当别论：首先对于一个问题你先要判断出这个问题是否能够用DP的思想来解决，那么可能有人会问了（谁？谁问了！出来见我！）怎么判断是否该用DP来解决呢？我的答案是…靠直觉（逃），实际上在上节课老师讲分治算法的时候就已经说过了类似的东西DP也差不多就是把一个大问题细分为小问题处理然后从小问题中不断得到最优的答案，从我个人的理解来说吧DP更像是从枚举里面挑选出当前最优的答案然后随着问题规模的扩大最后就能得到答案了（好像说了跟没说一样诶）。下面会介绍一下DP的几个特性。

DP特性：

1. 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。（简单来说就是要求要得到最优解的话你得得到子最优解的情况）
2. 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。（就是不能具有相互干扰的关系就是最优子结构的出来然后后面怎么选择不会对已经求出的最优子问题的结构进行一个破坏）
3. 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。（这个不多解释，等会记忆化搜索的时候就知道了）

上面劈里啪啦说了一大堆我不知道你们有没有看懂，反正对于我来说是没有看懂，我最烦那种文字工程的概述一大堆了，老烦人了！说到底还是自己太菜了看不懂

如何快速的掌握DP思想

据说，或者说对于我自己的认知来说想要训练好DP有两种

1. 你是个小天才，理解力过人，我觉得你不是（你再骂！ ）

2. 多做题吧，想想自己的高中难道不就是这么过来的吗？

首先在正式写DP之前先说一下我觉得如何能够高效的掌握DP，我觉得路径应该是这样子的：搜索——>记忆化搜索——>DP（我们今天讲01背包也是按照这个路线来说的），这种说法是我在自己做了一些题目之后鄙人自己感悟出来的，所以如果想要练习DP的同学萌可以按照这个练习路径来逐步强化。

科普外加share经验bb了半天，让我们直接暴力一点看题！！！

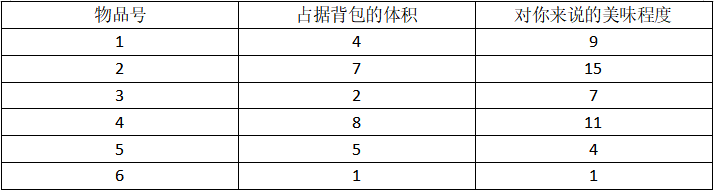
摆在你面前的是6种超好吃的零食，但你只有一个背包容量为8的背包（别想了，不准堂食只能外带）
w[i]表示第i种零食占据的体积，v[i]代表第i种零食好吃的程度
那么你应该如何选择零食才可以使得背包内装得下的零食的好吃程度总和最大呢！
以下是表格数据

因为我不知道你们到底喜欢吃什么所以就用物品号代替了

从贪心算法看01背包

首先一些会自己独立思考的人在第一次遇到背包问题的时候我想你们想的大概率是！
贪心算法！！！（大声告诉我我说得对吗？）但是实际上呢这个有很多的反例，这里要知道一件事贪心算法有的时候用来解题的话正确性很难得到一个证明，也就是所谓的玄学~

1. 如果我非常贪心的把所有零食按照对你来说的美味程度进行一个排序的话，那么是否我就能用我有限容量的背包得到最优情况呢？
   答案是不行！ 首先我们很容易知道该表格对应的最优答案应该是把物品1+物品3+物品6=17，如果按照美味程度排序的话那么会得到如下表格
   你会先把物品2装走这时候你发现背包只够装物品1了，然后你就GG了，因为你只拿走了了16个单位美味程度的物品，**
   

2. 这时候就有人说了，哦豁！那我按照背包体积来排序！得到的应该是最优的吧~
   嘿嘿，那你还真是个机（小）灵（笨）鬼（蛋），先简单想一下，我们要的目的是美味程度最优，那你拿背包最优干啥，這是一点但是肯定还有人不服气啊！那数据说话吧
   
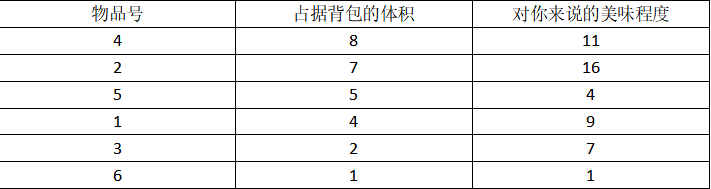
   从大到小的话我先拿8体积到背包发现不对诶，才11，那我从小到大拿嘻嘻~物品1+物品2+物品6…17！！！（Ohhhhhhhhhhhhhhhhhhhhhhhhhhhh）
   
   你以为你想法是对的？啊哈~又错了，可是为什么？！很简单你只需要把物品5和物品1的美味程度对调一下你就发现你输的一塌糊涂了[狗头保命]

3. 哼！那我还有第三种！那我选择性价比最高的物品然后贪心放进背包这样子总可以了吧，有图有真相好叭！
   
   很容易看出答案是物品3+物品1+物品6！！！woc又做对了**ohhhhhhhhhhhhhhhhhh！**但是呢实际上这还是错的hhhh，比如说我们有这么一组数据嗷：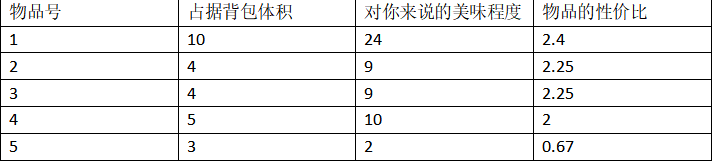
   然后给出的条件是背包最大容量为13，那么我们可以看出来就是我们会优先选择物品1，然后剩下的背包体积为3，所以遍历下来就只能选择说选择物品5，那么答案就是24+2=26，而实际上这题的最优解应该是选择物品2/3/4，然后体积刚好是13，而美味程度则是最大为9+9+10=28；哦豁，又双叒叕错了！泪目了55555，所以这种方法我们也pass掉了。
   
   综上所述，贪心算法至少在01背包问题上不太可行！

上面我们说过动态规划的实现分为两种，一种是迭代实现一种是递归实现，那么接下来就让我们走进递归的世界里~

自底向上递归搜索/暴力枚举

首先我们发现，对于每一个物品我们有两种状态，一种我不把这个物品放进背包里面，另一种是我要把这个物品放进背包里面，那么这里细说的话实际上是由三种情况的：

1. 背包容量允许的情况下我把这个物品放进背包
2. 背包容量允许的情况下我不把物品放进背包
3. 背包容量不允许的情况下我也把物品放进背包 被迫只得不把物品放进背包

那么是不是对于所有的物品的可能的所有的放进背包的情况是2^n 次方，诶没错在这个时候你就发现了这个递归搜索的一个时间复杂度，那可能这时候会说了但是有些情况是不可以的鸭！比如全部物品都选了的时候那可是背包容量有限的啊，你这不是摆明着骗我呢嘛？诶对了！这就涉及到了搜索中的一个剪枝问题，那么怎么个剪枝法呢上代码！

#include 
#define maxn 15
using namespace std;
int n,cap;//（c代表着capacity）
int v[maxn],w[maxn];//v代表占据的体积，w代表物品的价值
int ans=0;
void dfs(int x,int left,int cur){
    //传递了三个参数分别代表了编号为x的物品，在背包当前剩下的容量left
    //以及当前容量下的最大价值
    if(left<=0||x>n){//当剩余容量不足或者编号超过n的时候结束递归调用
        ans=max(ans,cur);//此时比较ans与当前的最大价值
        return;
    }
    if(left-v[x]>=0)//剩余容量能够装下这个物品
        dfs(x+1,left-v[x],cur+w[x]);//对应上述三种情况的第一种
    dfs(x+1,left,cur);//对应上述三种情况的后两种
}
int main()
{
    cin>>n>>cap;//输入两个值
    for(int i=1;i<=n;i++){
        cin>>w[i]>>v[i];//输入每一个物品的价值和所占据的体积
    }
    dfs(1,cap,0);
    cout<<ans<<endl;//打印最后的结果
}

自顶向下递归回溯

以上其实是一种自底向上的一种递归，但是要想要真正迈入今天的正统记忆化搜索以及迭代的动态规划的话得看另外一种写法，这种写法是我在老师的PDF上看到的伪码自己实现的（当时还觉得自己现在写的这种搜索好像不能实现记忆化是不是写错了）

那么自顶向下的递归搜索和上面有点不一样，见如下代码：

#include 
#define maxn 15
using namespace std;
int n,cap;
int v[maxn],w[maxn];
int ans=0;
int dfs(int num,int c){
    if(c<0) return -100000;//这里需要特别注意一下不是返回0而是一个较大的负值
    if(num<1)return 0;//如果物品编号小于1则返回因为不存在0号物品
    return max(dfs(num-1,c-v[num])+w[num],dfs(num-1,c));
}
int main()
{
    cin>>n>>cap;
    for(int i=1;i<=n;i++){
        cin>>w[i]>>v[i];
    }
    cout<<dfs(n,cap);//代表有从n种物品选出填满容量为cap的背包的最大价值
}

这时候发现dfs函数返回值为int类型，然后再来看一下其函数的核心，第一行c<0代表说如果当前的背包容量为负数或者为0了那我返回一个类似于无穷大的数，这里可能有些人表示奇怪，甚至我自己第一次写的时候也上套了，为什么不是返回0而是返回一个负无穷大的数呢，原因其实很简单，我们可以这么理解嗷， 我先来假设一种情况：

当我背包容量为3的时候，此时我只有一个体积为3，美味程度为4的物品可供选择，那么背包能获取到的最大美味程度是多少

答案应该是0对吧，那么如果我们原先当c<0时候return 0会是什么结果呢，很简单只进行一层递归，也就是得到了结果为max（0+w[num]，0）那很显然明明是装不下的东西却被装下了，这显然是不对的，是吧。

那你可能会问为什么num<1不返回负值呢，原因也很简单，那我再举一个情况：

当我背包容量为3的时候，此时只有一个体积为2，美味程度为2的物品可供选择，那么背包能获取到的最大美味程度是多少

这时候如果num<1返回无穷大的时候结果应该是为max（-∞+w[num],0）；这显然也不对啊，我明明把物品放进去了啊为什么值这么扯淡啊，对吧，所以这时候要返回一个0。然后最后就是return语句了，可以看到这里用了一个max（）比较函数，前者是对于第n个物品选的情况，后者是不选第n个物品的情况，最后输出结果是一样的。（某种程度来说这个和老师的分治有一点点像吧，但是实际上显然那不是啊，因为分治是分为规模一致的子问题，这个显然规模不一致）。

记忆化搜索/带备忘录的递归

上面说的就是自顶向下递归求解的做法了，既然都到了这一步了那么就开始讲述我们的记忆化搜索了，这时候先上一张图好吧

这里我们可以注意到有很多相同的子问题，那么我们考虑是否可以把一些已经做过的递归把它记起来呢？于是乎就产生了下面代码：

#include 
#define maxn 15
using namespace std;
int n,cap;
int v[maxn],w[maxn],dp[maxn][maxn];
int ans=0;
int dfs(int num,int c){
    if(dp[num][c])return dp[num][c];//若该子问题已经计算过则直接返回（剪枝操作）
    if(c<=0) return -100000;
    if(num<1)return 0;
    dp[num][c]= max(dfs(num-1,c-v[num])+w[num],dfs(num-1,c));
    //记录当前情况的最优解
    return dp[num][c];//返回最优解供上一级调用
}
int main()
{
    cin>>n>>cap;
    for(int i=1;i<=n;i++){
        cin>>w[i]>>v[i];
    }
    cout<<dfs(n,cap)<<endl;
}

可以看到这个和刚刚的搜索非常的相似，为数不多不同的地方是递归入口被我们改动了，如果进入递归发现当前参数下的子问题已经被计算过一次了，那么我们直接将结果回溯给上一级调用，这样子就剪掉了很多重复的计算，你可能觉得这个好像作用不是特别大，但是当n的规模逐步扩大的时候，这个优化的效率的好处就不是一点两点了。

DP中的四大难点

讲到现在~我们把DP的两种形式之一的递归全部讲完了，那么我们来看看迭代的动态规划，讲到了真正的DP，那么我就来说一下我认为的DP四大元素：

1. 定义DP的维度和含义
2. 找到对应的状态转移方程
3. 一定的初始化条件
4. 迭代顺序问题

01背包二维DP实现

首先先定义怎么下呢，基本上来说DP的定义就是你要什么和你给出了什么条件我就下什么样的定义，那么对于01背包来说的话呢就是这么下定义的。

dp[i][j]代表当背包容量为j时候前i个物品能够达到的最大美味程度是多少

然后找状态转移方程，是什么呢？很简单，其实就是我们记忆化搜索中的那个状态转移方程，dp[i][j]=max(dp[i-1][j],dp[i-1][c-v[i]]+w[i]);但是细心的小伙伴可能发现一个问题了，对于体积超过当前容量二导致不能够存放该物品的情况怎么办呢？搜索的时候我们是返回一个无穷大的值而在这边我们是怎么处理的呢？答案显然就是上一种情况也就是上一种情况对应的值鸭。那么说到这里我们DP四大难点中的两大难点就都搞明白了，。

还有两个难点分别是一定的初始化条件但是呢实际上通过这个问题是看不出来初始化的一个重要性的，这个问题可以等到大家以后做题的时候可以用来自己归纳总结一下，我是遇到过很多我其他三个难点都解决了但是死在了DP的初始化上面，这个我后面讲到优化的时候会给大家补充这个地方的知识点的。然后我们先继续看一下DP 的第四个难点，迭代顺序问题，首先对于i来说的话呢实际上从小到大和从大到小没有什么太大的问题，因为i代表的是物品的一个编号嘛，没有什么实质性的大差别，那么对于j呢，诶好像也是从大到小和从小到大没有什么差别诶？是吗？我们来插入一个表格：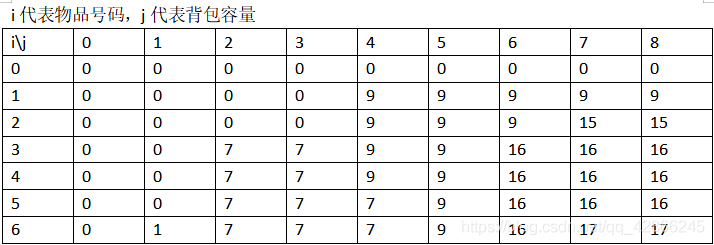
通过这个表格我们可以发现表单里面的每一个单元格的值只会跟上一个式子里面的dp[i-1][j]和dp[i-1][j-v[i]]的值有关，所以不管j是从大到小还是从小到大都没有什么差别。那么我们就可以写出如下的代码了。。。。。吧？

#include 
#include 
#define maxn 15
using namespace std;
int n,cap;
int v[maxn],w[maxn],dp[maxn][maxn];
int main()
{
    cin>>n>>cap;
    for(int i=1;i<=n;i++){
        cin>>w[i]>>v[i];
    }
    for(int i=1;i<=n;i++){
        for(int j=cap;j>=0;j--){
            if(j<v[i])
                dp[i][j]=dp[i-1][j];
            else
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);
        }
    }
    cout<<dp[n][cap]<<endl;
}

好，看似到这里DP就告一段落了，但是，真的那么简单嘛？你以为01背包就这？那必不可能

DP优化相关

我们仔细看看这种做法的时间复杂度是多少呢？很显然，O（n^{2）对吧，相比暴力枚举的2}n的复杂度来说已经进步很大了呢！那我们有办法再让它变得更快嘛？我不知道，可能有吧，但是我不清楚哈哈哈哈哈，我知道的是我们可以让它的空间复杂度更低，因为我们现在可以发现说目前的空间复杂度是O（n^2），虽然我们都知道现在硬件很发达，基本上来说对于一个算法来说考虑时间复杂度更多于考虑空间复杂度，但是我们是在写一个算法呢对吧，题目有限制怎么办呢？比如说我限制了你的内存空间，那么当n变得很大的时候这时候程序向内存申请就超过了，那么怎么降低空间复杂度呢？机智的小伙伴们或许已经从上面的表格的出来的结论发现：我们每一次dp要用的值都只和上一行的结果里面需要的值进行调取，而上上行，甚至于上上上好几行都没有存在的必要性，而且我们要的最后的结果就是最后一行的最后一个，那么我们开那么多空间干嘛鸭？直接进行覆盖存储不就好了吗？也就是所谓的“滚动数组”，那么这时候就上代码~

#include 
#include 
#define maxn 15
using namespace std;
int n,cap;
int v[maxn],w[maxn],dp[maxn];
int main()
{
    cin>>n>>cap;
    for(int i=1;i<=n;i++){
        cin>>w[i]>>v[i];
    }
    for(int i=1;i<=n;i++){
        for(int j=cap;j>=v[i];j--){
            dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
        }
    }
    cout<<dp[cap]<<endl;
}

再次钻研代码会发现这次代码好像你都懂了，只有一个地方不一样那就是j的遍历变成了从大到小了，诶我觉得很不舒服我要按照我自己的风格来，你一改，哦豁!答案不一样了，這是为什么呢？这里的j必须是从大到小遍历，这里我就不上表格解释了，而是引申处另一个知识点，上面我们使用表格来说明是因为更容易解释，而这里直接用定义解释更方便一点，先说一下结论，结论就是从大到小遍历是为了能够保证每一个物品只取了一次而不是取了好几个，为什么呢？照样啊我们用例子说话

假设我们只有一个物品，容量为2，美味程度为4，这时候我们有一个容量为6的背包，那么背包能获取到的最大美味程度是多少

当我容量为2的时候我最大价值为dp[0]=4
当我容量为4的时候我最大价值为dp[2]+4=8
当我容量为6的时候，最大价值为dp[4]+4=12；
**我的天哪！！！**越来越糟，我明明只能取一次的物品被我去了多次！这不是违反题意了吗？所以我们要逆着遍历。

那么为什么逆着能够保证只取了一次呢？
因为你会发现，当你的当前的背包容量j大于当前物品的体积的时候，每一次使用的都是上一行相应情况的最优解（也就是dp[j-v[i]]加上当前的值，而之前顺着来的话每一次调用的就是本行的最优解然后再叠加在上面，或者换一种说法来说就是你dp[j]要更新需要用到的是上一行的值，而由于现在dp数组被我们定义为了一维，如果我们不逆着遍历的话，那么你顺序遍历用的永远是当前行的值而不是上一行的。这就是为什么我们之前说二维的情况下对于j的遍历顺序或者逆序遍历都可以，而这边只能采取逆序遍历，因为对于前者的情况来说不管顺序还是逆序遍历最后得到的结果都是一样因为用的都是表格种上一行的结果，而当前情况下如果使用顺序就会破坏这种结构。

**那么到这里dp01问题就讲完了…吗？并没有，还记得我之前说过的初始化问题吗？**我来填坑了，初始化其实非常的坑人，举个例子吧，对于01背包来说呢题目可以给你两种限制就是说

1. 我今天必须把背包全带走的情况下我要拿到对应的最大美味程度
2. 我只要能够拿到最大的美味程度的背包的物品就好了，我不管背包装满了没

两种情况下的初始化是不一样的

1. 前者的初始化为dp[0]=0;dp[1-w]=-INF
2. 后者的初始化为dp[0-v]=0；

为什么呢，很容易理解，从字面上来说就是前者就是除了背包容量为0的时候其他时候你都还没有装满物品，那么你现在就是负无穷大代表没有当前没有答案，后者就是说我不管你装满了没有已经是0也就是说我0也可以是一种答案就是物品装不进去对吧，这其实还算是比较简单的初始化问题了。

浅谈完全背包问题

最后我来重复一点迭代顺序问题，我们上面说过了当我们不小心把一维的DP01背包问题的代码的迭代顺序反了之后就会出现一个物品取多次时候的当前背包容量的最大值，那么巧了~这个在动态规划上又是另外一个经典问题，那就是完全背包问题。

这里给出完全背包问题的定义，给出n种物品以及他们的美味程度和所占据的体积，且每一个物品不限量，那么问给定固定容量的背包请求出相应的最大的美味程度

那么以上就是全部的解释了，该不会有人看到现在还不懂背包问题吧？不会吧？！谢谢各位客官能够看我废话半天到这里，顺手给个赞可好~