计算机视觉(七)——多视几何初步尝试
基础矩阵原理
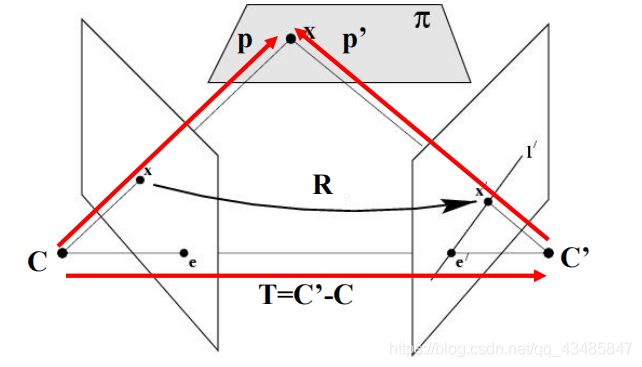
如上图,在平面π中存在一个点X,C和C’分别是两个不同角度相机的光心。那么,X就会分别投影在两个相机的图像上为x,x’。如果我们已知基础矩阵,以及X点在一个像平面的坐标x,那么就能够算出X点在另一个像平面的投影坐标x’。基础矩阵的作用就描述了空间中的点在不同像平面坐标的对应关系。
根据上篇博文的相机拍摄的原理,可以知道空间中的点通过确定在世界坐标中的值,以及相机参数矩阵K可以算出该点在像平面的值。如图所示

K和K’分别是两个相机的参数矩阵。p和p’是X在平面π的坐标表示。所以可以得出
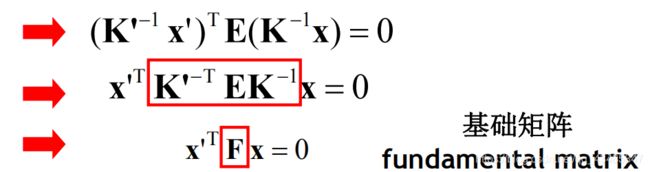
其中的E为本质矩阵,其描述了空间中点X在两个坐标系的坐标对应关系。而其求解过程根据三线共面(CC’,C’p’,Cp)可以得到

具体计算过程

代码实现
1.这段代码是实现两张图像的基础矩阵求解。以及寻找最佳匹配。
#!/usr/bin/env python
# coding: utf-8
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
from imp import reload
# In[2]:
import importlib
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift
camera = reload(camera)
homography = reload(homography)
sfm = reload(sfm)
sift = reload(sift)
# Read features
im1 = array(Image.open('E:/Py_code/photo/ch5_1/t1.jpg'))
sift.process_image('E:/Py_code/photo/ch5_1/t1.jpg', 'im1.sift')
l1, d1 = sift.read_features_from_file('im1.sift')
im2 = array(Image.open('E:/Py_code/photo/ch5_1/t2.jpg'))
sift.process_image('E:/Py_code/photo/ch5_1/t2.jpg', 'im2.sift')
l2, d2 = sift.read_features_from_file('im2.sift')
matches = sift.match_twosided(d1, d2)
ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)
x1n = x1.copy()
x2n = x2.copy()
print (len(ndx))
figure(figsize=(16, 16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()
# Chapter 5 Exercise 1
# Don't use K1, and K2
# def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
""" Robust estimation of a fundamental matrix F from point
correspondences using RANSAC (ransac.py from
http://www.scipy.org/Cookbook/RANSAC).
input: x1, x2 (3*n arrays) points in hom. coordinates. """
from PCV.tools import ransac
data = np.vstack((x1, x2))
d = 20 # 20 is the original
# compute F and return with inlier index
F, ransac_data = ransac.ransac(data.T, model, 8, maxiter, match_threshold, d, return_all=True)
return F, ransac_data['inliers']
# find E through RANSAC
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-2)
print (len(x1n[0]))
print (len(inliers))
P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)
# triangulate inliers and remove points not in front of both cameras
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)
# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)
figure()
imshow(im1)
gray()
plot(x1p[0], x1p[1], 'o')
# plot(x1[0], x1[1], 'r.')
axis('off')
figure()
imshow(im2)
gray()
plot(x2p[0], x2p[1], 'o')
# plot(x2[0], x2[1], 'r.')
axis('off')
show()
figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))
imshow(im3)
cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
if (0 <= x1p[0][i] < cols1) and (0 <= x2p[0][i] < cols1) and (0 <= x1p[1][i] < rows1) and (0 <= x2p[1][i] < rows1):
plot([x1p[0][i], x2p[0][i] + cols1], [x1p[1][i], x2p[1][i]], 'c')
axis('off')
show()
print (F)
# Chapter 5 Exercise 2
x1e = []
x2e = []
ers = []
for i, m in enumerate(matches):
if m > 0: # plot([locs1[i][0],locs2[m][0]+cols1],[locs1[i][1],locs2[m][1]],'c')
p1 = array([l1[i][0], l1[i][1], 1])
p2 = array([l2[m][0], l2[m][1], 1])
# Use Sampson distance as error
Fx1 = dot(F, p1)
Fx2 = dot(F, p2)
denom = Fx1[0] ** 2 + Fx1[1] ** 2 + Fx2[0] ** 2 + Fx2[1] ** 2
e = (dot(p1.T, dot(F, p2))) ** 2 / denom
x1e.append([p1[0], p1[1]])
x2e.append([p2[0], p2[1]])
ers.append(e)
x1e = array(x1e)
x2e = array(x2e)
ers = array(ers)
indices = np.argsort(ers)
x1s = x1e[indices]
x2s = x2e[indices]
ers = ers[indices]
x1s = x1s[:20]
x2s = x2s[:20]
# In[25]:
figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))
imshow(im3)
cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1s)):
if (0 <= x1s[i][0] < cols1) and (0 <= x2s[i][0] < cols1) and (0 <= x1s[i][1] < rows1) and (0 <= x2s[i][1] < rows1):
plot([x1s[i][0], x2s[i][0] + cols1], [x1s[i][1], x2s[i][1]], 'c')
axis('off')
show()
这是图像的sift的匹配结果

这两张是这些点的三维位置的信息


以及sift的匹配结果

通过算法修改之后的sift的特征匹配

发现修改之后,sift的匹配能取得更好的效果。
2.三维点和照相机矩阵
# coding: utf-8
# In[1]:
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
# In[2]:
from PCV.geometry import homography, camera, sfm
from PCV.localdescriptors import sift
# In[5]:
# Read features
im1 = array(Image.open('E:/Py_code/photo/ch5_1/6.jpg'))
sift.process_image('E:/Py_code/photo/ch5_1/6.jpg', 'im1.sift')
im2 = array(Image.open('E:/Py_code/photo/ch5_1/7.jpg'))
sift.process_image('E:/Py_code/photo/ch5_1/7.jpg', 'im2.sift')
# In[6]:
l1, d1 = sift.read_features_from_file('im1.sift')
l2, d2 = sift.read_features_from_file('im2.sift')
# In[7]:
matches = sift.match_twosided(d1, d2)
# In[8]:
ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)
d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()
# In[9]:
figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()
# In[10]:
#def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
""" Robust estimation of a fundamental matrix F from point
correspondences using RANSAC (ransac.py from
http://www.scipy.org/Cookbook/RANSAC).
input: x1, x2 (3*n arrays) points in hom. coordinates. """
from PCV.tools import ransac
data = np.vstack((x1, x2))
d = 10 # 20 is the original
# compute F and return with inlier index
F, ransac_data = ransac.ransac(data.T, model,8, maxiter, match_threshold, d, return_all=True)
return F, ransac_data['inliers']
# In[11]:
# find F through RANSAC
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-1)
print(F)
# In[12]:
P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)
# In[13]:
print(P2)
print(F)
# In[14]:
# P2, F (1e-4, d=20)
# [[ -1.48067422e+00 1.14802177e+01 5.62878044e+02 4.74418238e+03]
# [ 1.24802182e+01 -9.67640761e+01 -4.74418113e+03 5.62856097e+02]
# [ 2.16588305e-02 3.69220292e-03 -1.04831621e+02 1.00000000e+00]]
# [[ -1.14890281e-07 4.55171451e-06 -2.63063628e-03]
# [ -1.26569570e-06 6.28095242e-07 2.03963649e-02]
# [ 1.25746499e-03 -2.19476910e-02 1.00000000e+00]]
# In[15]:
# triangulate inliers and remove points not in front of both cameras
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)
# In[16]:
# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)
# In[17]:
figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))
imshow(imj)
cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
if (0<= x1p[0][i]图像1和2的sift匹配

得到的基础矩阵和相机矩阵

通过修正之后的sift匹配(吐槽下集大的建筑,太多相似的地方了,有时候的sift匹配会出现错配,不过平时确实颜值在线)

图像2和3的sift匹配

通过之前做过的修正,发现2和3的匹配对少。可能需要我们慢慢的调节代码的参数来改变这情况。

