opencv-python SIFT(Scale-Invariant Feature Transform)简介

目标：

• 了解SIFT算法的概念
• 学习如何找到SIFT关键点和描述符。

理论

在上一小节中，我们看到了一些角点探测器，如Harris角点探测器等。它们具有旋转不变的特性，这意味着，即使图像旋转，我们也可以找到相同的角点。很明显，因为角落在旋转的图像中也是角点。但是缩放呢？如果缩放图像，则角点可能不是角点。例如，检查下面的简单图像。当在同一窗口中放大时，小窗口内的小图像中的角是平坦的。所以Harris的角点不是规模不变的。

因此，2004年，不列颠哥伦比亚大学D.Lowe在他的论文中提出了一种新的算法，尺度不变特征变换（SIFT），从尺度不变关键点的独特图像特征，提取关键点并计算其描述符。（本文易于理解并被认为是SIFT上最好的材料。所以这个解释只是本文的简短摘要）。

SIFT算法主要涉及四个步骤。我们将逐一看到它们。

尺度空间极值检测

从上图我们可以很明显的看出来在不同的尺度空间不能使用相同的窗口检测极值点。对小的角点要用小的窗口，对大的角点只能使用大的窗口。为了达到这个目的我们要使用尺度空间滤波器。（尺度空间滤波器可以使用一些列具有不同方差$$\sigma$$的高斯卷积核构成）。使用具有不同方差值$$\sigma$$的高斯拉普拉斯算子（LoG）对图像进行卷积，LoG 由于具有不同的方差值$$\sigma$$所以可以用来检测不同大小的斑点（当 LoG 的方差$$\sigma$$与斑点直径相等时能够使斑点完全平滑）。简单来说方差$$\sigma$$就是一个尺度变换因子。例如，上图中使用一个小方差$$\sigma$$的高斯卷积核是可以很好的检测出小的角点，而使用大方差$$\sigma$$的高斯卷积核时可以很好的检测除大的角点。所以我们可以在尺度空间和二维平面中检测到局部最大值，如$$(x,y,\sigma )$$, 这表示在$$\sigma$$尺度中$$(x,y)$$点可能是一个关键点。（高斯方差的大小与窗口的大小存在一个倍数关系：窗口大小等于 6 倍方差加 1，所以方差的大小也决定了窗口大小）

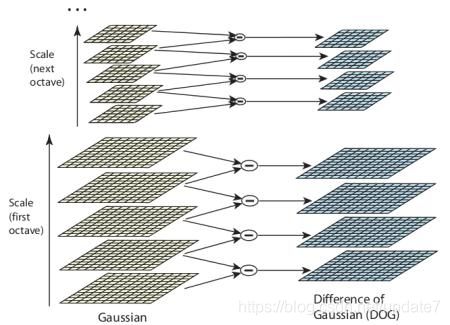
但是这个 LoG 的计算量非常大，所以 SIFT 算法使用高斯差分算子（DoG）来对 LoG 做近似。这里需要再解释一下图像金字塔，我们可以通过减少采样（如只取奇数行或奇数列）来构成一组图像尺寸（1，0.5，0.25 等）不同的金字塔，然后对这一组图像中的每一张图像使用具有不同方差$\sigma$的高斯卷积核构建出具有不同分辨率的图像金字塔（不同的尺度空间）。DoG 就是这组具有不同分辨率的图像金字塔中相邻的两层之间的差值。如下图所示：

在 DoG 搞定之后，就可以在不同的尺度空间和 2D 平面中搜索局部最大值了。对于图像中的一个像素点而言，它需要与自己周围的 8 邻域，以及尺度空间中上下两层中的相邻的 18（2x9）个点相比。如果是局部最大值，它就可能是一个关键点。基本上来说关键点是图像在相应尺度空间中的最好代表。如下图所示：

该算法的作者在文章中给出了 SIFT 参数的经验值：octaves=4（通过降低采样从而减小图像尺寸，构成尺寸减小的图像金字塔，尺度空间为 5，也就是每个尺寸使用 5 个不同方差的高斯核进行卷积，初始方差是 1.6，$\sigma =1.6$,$k=\sqrt{2}$等作为最优值。

关键点（极值点）定位

一旦找到关键点，我们就要对它们进行修正从而得到更准确的结果。可以使用尺度空间的泰勒级数展开来获得极值的准确位置，如果极值点的灰度值小于阈值（0.03）就会被忽略掉。在 OpenCV 中这种阈值被称为contrastThreshold。

DoG 算法对边界非常敏感，所以我们必须要把边界去除。前面我们讲的Harris 算法除了可以用于角点检测之外还可以用于检测边界。作者就是使用了同样的思路。作者使用 2x2 的 Hessian 矩阵计算主曲率。从 Harris 角点检测的算法中，我们知道当一个特征值远远大于另外一个特征值时检测到的是边界。

所以他们使用了一个简单的函数，如果比例高于阈值（OpenCV 中称为边界阈值），这个关键点就会被忽略。文章中给出的边界阈值为 10。

所以低对比度的关键点和边界关键点都会被去除掉，剩下的就是我们感兴趣的关键点了。

为关键点（极值点）指定方向参数

现在我们要为每一个关键点赋予一个反向参数，这样它才会具有旋转不变性。获取关键点（所在尺度空间）的邻域，然后计算这个区域的梯度级和方向。根据计算得到的结果创建一个含有 36 个 bins（每 10 度一个 bin）的方向直方图。（使用当前尺度空间$$\sigma$$值的 1.5 倍为方差的圆形高斯窗口和梯度级做权重）。直方图中的峰值为主方向参数，如果其他的任何柱子的高度高于峰值的80% 被认为是辅方向。这就会在相同的尺度空间相同的位置构建除具有不同方向的关键点。这对于匹配的稳定性会有所帮助。

关键点描述符

新的关键点描述符被创建了。选取与关键点周围一个 16x16 的邻域，把它分成 16 个 4x4 的小方块，为每个小方块创建一个具有 8 个 bin 的方向直方图。总共加起来有 128 个 bin。由此组成长为 128 的向量就构成了关键点描述符。除此之外还要进行几个测量以达到对光照变化，旋转等的稳定性。

关键点匹配

下一步就可以采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取第一个图的某个关键点，通过遍历找到第二幅图像中的距离最近的那个关键点。但有些情况下，第二个距离最近的关键点与第一个距离最近的关键点靠的太近。这可能是由于噪声等引起的。此时要计算最近距离与第二近距离的比值。如果比值大于 0.8，就忽略掉。这会去除 90% 的错误匹配，同时只去除 5% 的正确匹配。如文章所说。
这就是 SIFT 算法的摘要。非常推荐你阅读原始文献，这会加深你对算法的理解。请记住这个算法是受专利保护的。所以这个算法包含在 OpenCV 中的收费模块中。

OpenCV中的SIFT

现在让我们来看看 OpenCV 中关于 SIFT 的函数吧。让我们从关键点检测和绘制开始吧。首先我们要创建对象。我们可以使用不同的参数，这并不是必须的，关于参数的解释可以查看文档。

import numpy as np
import cv2 as cv

img = cv.imread('home.jpg')
gray= cv.cvtColor(img,cv.COLOR_BGR2GRAY)

sift = cv.xfeatures2d.SIFT_create()
kp = sift.detect(gray,None)

img=cv.drawKeypoints(gray,kp,img)

cv.imwrite('sift_keypoints.jpg',img)

函数 sift.detect() 可以在图像中找到关键点。如果你只想在图像中的一个区域搜索的话，也可以创建一个掩模图像作为参数使用。返回的关键点是一个带有很多不同属性的特殊结构体，这些属性中包含它的坐标(x，y)，有意义的邻域大小，确定其方向的角度、指定关键点强度的响应等。

OpenCV也提供了绘制关键点的函数：cv2.drawKeyPoints()，它可以在关键点的部位绘制一个小圆圈。如果你设置参数为cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS，就会绘制代表关键点大小的圆圈甚至可以绘制除关键点的方向。见下面的例子。

img=cv.drawKeypoints(gray,kp,img,flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
cv.imwrite('sift_keypoints.jpg',img)

结果如下图所示：

现在要计算描述符，OpenCV提供了两种方法。

1. 由于你已经找到了关键点，因此可以调用sift.compute()来计算我们找到的关键点的描述符。例如：kp，des = sift.compute（灰色，kp）
2. 如果你没有找到关键点，请使用函数sift.detectAndCompute()在一个步骤中直接查找关键点和描述符。

我们将看到第二种方法：

sift = cv.xfeatures2d.SIFT_create()
kp, des = sift.detectAndCompute(gray,None)

这里kp是关键点列表，des是形状为$$Number\_of\_Keypoints\times 128$$的numpy数组。

所以我们得到了关键点，描述符等。现在我们想看看如何匹配不同图像中的关键点。 我们将在接下来的章节中学习。