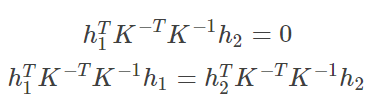标定手机相机参数

本文利用张正友相机标定方法，标定手机相机的相关参数。手机型号：华为mate8

1,张正友相机标定实验原理
 

（1）计算单应性矩阵

  设三维世界坐标的点为X=[X,Y,Z,1]TX=[X,Y,Z,1]T，二维相机平面像素坐标为m=[u,v,1]Tm=[u,v,1]T，所以标定用的棋盘格平面到图像平面的单应性关系为： 

                                                                             

其中s为尺度因子，K为摄像机内参数，R为旋转矩阵，T为平移向量。令 

                                                             

注意，s对于齐次坐标来说，不会改变齐次坐标值。张氏标定法中，将世界坐标系狗仔在棋盘格平面上，令棋盘格平面为Z=0的平面。则可得 

                                   

我们把K[r1, r2, t]叫做单应性矩阵H，即 

                                                            

H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H。

(2)计算内参矩阵

 由上式可得 

                                                                     

 

由于旋转矩阵是个酉矩阵，r1和r2正交，可得     

代入可得：

 

即每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算，定义如下： 

 可以看到，B是一个对称阵，所以B的有效元素为六个，让这六个元素写成向量b，即 

 

可以推导得到 

 利用约束条件可以得到： 

 

通过上式，我们至少需要三幅包含棋盘格的图像，可以计算得到B，然后通过cholesky分解，得到相机的内参数矩阵K

（3）计算外部参数矩阵

根据以上推导的：

（4）最大似然估计

上述的推导结果是基于理想情况下的解，但由于可能存在高斯噪声，所以可以使用最大似然估计进行优化。 

（5）径向畸变估计

 张氏标定法只关注了影响最大的径向畸变。

2，标定步骤

 （1）打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上

 （2）针对棋盘格拍摄若干张图片（一般10-20张） 本实验用11张图片

 （3）在图片中检测特征点（Harris特征）

（4）利用解析解估算方法计算出5个内部参数，以及6个外部参数

  (5)根据极大似然估计策略，设计优化目标并实现参数的refinement

3,python-opencv实现

import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((9*13, 3), np.float32)
objp[:, :2] = np.mgrid[0:9, 0:13].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob("D:/img/*.jpg")
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (9, 13), None)
    print(ret)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5,5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (9,13), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        cv2.imshow('img', img)
        cv2.waitKey(1550)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")

实验结果：

内参矩阵K：

 

畸变系数：

 

旋转向量：

rvecs:
 [array([[-0.15498336],
       [ 0.08299058],
       [ 1.57825619]]), array([[-0.17700503],
       [ 0.13513091],
       [ 1.54444289]]), array([[-0.1969227 ],
       [ 0.06791505],
       [ 1.42547299]]), array([[-0.10582712],
       [ 0.13866824],
       [ 1.57904503]]), array([[-0.10027729],
       [ 0.14172248],
       [ 1.66829567]]), array([[-0.06210765],
       [ 0.13368951],
       [ 1.52657835]]), array([[-0.09108756],
       [ 0.08716393],
       [ 1.55527437]]), array([[-0.1503406 ],
       [ 0.07851393],
       [ 1.53904991]]), array([[-0.14010565],
       [ 0.13986868],
       [ 1.54698176]]), array([[-0.18304361],
       [ 0.05257621],
       [ 1.55159216]]), array([[-0.07789582],
       [-0.19367696],
       [-1.60933796]])]

平移向量：
tvecs:
 [array([[ 6.49072436],
       [-5.29625546],
       [15.25918388]]), array([[ 7.52990441],
       [-3.88858914],
       [21.47230557]]), array([[ 2.43990326],
       [-5.85870394],
       [21.46053901]]), array([[ 6.28452525],
       [-4.70325779],
       [14.08126117]]), array([[ 5.41459937],
       [-4.1338246 ],
       [16.91337961]]), array([[ 4.72644156],
       [-5.75589647],
       [17.69613248]]), array([[ 8.32334749],
       [-5.98643736],
       [18.55356728]]), array([[ 6.7718184 ],
       [-4.97348129],
       [19.848855  ]]), array([[ 7.49688689],
       [-5.10980997],
       [19.88458187]]), array([[ 4.38663715],
       [-5.9598907 ],
       [21.18326816]]), array([[-4.84527183],
       [ 3.73164533],
       [19.56180214]])]

4，标定注意事项：

以下问题是由于标定的角点数错误造成，代码里的9*13表示棋盘格里的内角点数

 Traceback (most recent call last):
  File "D:/python计算机视觉/Camare_test.py", line 42, in
    ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
cv2.error: OpenCV(3.4.2) C:\projects\opencv-python\opencv\modules\calib3d\src\calibration.cpp:3143: error: (-215:Assertion failed) ni == ni1 in function 'cv::collectCalibrationData'

参考文章：

https://blog.csdn.net/u010128736/article/details/52860364

https://blog.csdn.net/a6333230/article/details/83478064