图像到图像的映射-仿射变换的应用-图像扭曲实例
图像到图像的映射-仿射变换的应用-图像扭曲实例
- 1. 原理
- 2.代码实现
1. 原理
单应性变换:
单应变换矩阵是一个3*3的矩阵H。这个变换可以被任意乘上一个非零常数,而不改变变换本身。所以它虽然具有9个元素,但是具有8个自由度。这意味这它里面有8个未知参数待求。
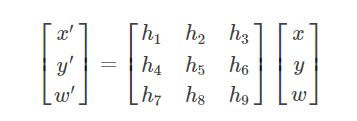
仿射变换
仿射变换:(Affine Transformation 或Affine Map)是一种二维坐标(x, y)到二维坐标(u, v)的线性变换,其数学表达式形式如下:
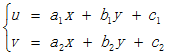
对应的齐次坐标矩阵表示形式为:

仿射变换保持了二维图形的“平直性”(直线经仿射变换后依然为直线)和“平行性”(直线之间的相对位置关系保持不变,平行线经仿射变换后依然为平行线,且直线上点的位置顺序不会发生变化)。非共线的三对对应点确定一个唯一的仿射变换。
α通道:
阿尔法通道是一个8位的灰度通道,该通道用256级灰度来记录图像中的透明度信息,定义透明、不透明和半透明区域。如果一个像素的alpha通道数值为0,那它就是完全透明的(也就是看不见的),而数值为1则意味着一个完全不透明的像素(传统的数字图像)。我们常说的RGBA图像就是普通的RGB加上这个α通道。
2.代码实现
代码:
# -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import Image
from pylab import *
from scipy import ndimage
# example of affine warp of im1 onto im2
im1 = array(Image.open('book1.jpg').convert('L'))
im2 = array(Image.open('jiageng2.jpg').convert('L'))
# set to points
tp = array([[120,260,260,120],[16,16,305,305],[1,1,1,1]])#变换的目标坐标
#tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)#函数内部warp
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)
# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# compute H
H = homography.Haffine_from_points(tp2,fp2)#
im1_t = ndimage.affine_transform(im1,H[:2,:2],(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])#图像alpha通道
im3 = (1-alpha)*im2 + alpha*im1_t
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()

