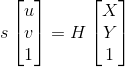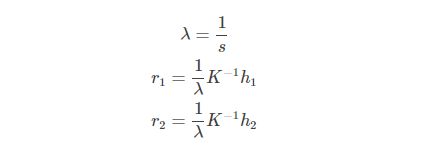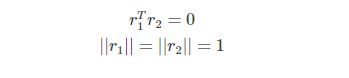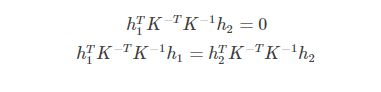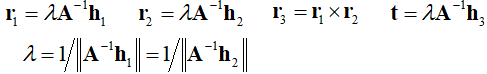照相机标定

目录

一 、相机标定介绍

1.1计算单应性矩阵H

1.2计算内参数矩阵

1.3计算外参数矩阵

二、实验过程

2.1实验步骤

2.2实现

2.3实验结果

三、实验总结

---

一 、相机标定介绍

相机标定是从三维点转换到二维点的过程，其目的是计算出该照相机的内、外参数，以及畸变参数。标定照相机的标准方法是，拍摄多幅平面棋盘模式的图像，然后进行处理计算。

基本参数设定
s：世界坐标系到图像坐标系的尺度因子
(u0,v0)：像主点坐标
α, β：焦距与像素横纵比的融合
γ：径向畸变参数
2D 图像点：
3D 空间点：

1.1计算单应性矩阵H

设三维世界坐标的点为，二维相机平面像素坐标为，所以标定用的棋盘格平面到图像平面的单应性关系为：

其中s为尺度因子，K为摄像机内参数，R为旋转矩阵，T为平移向量。令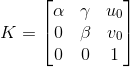

注意，s对于齐次坐标来说，不会改变齐次坐标值。张氏标定法中，将世界坐标系在棋盘格平面上，令棋盘格平面为Z=0的平面。则可得

我们把K[r1, r2, t]叫做单应性矩阵H，即

      H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H。

1.2计算内参数矩阵

由上面式子可得

r1和r2正交，可得

代入可得

1.3计算外参数矩阵

外部参数可通过Homography求解，由 H = [h1 h2 h3] = λA[r1 r2 t]，可推出

一般而言，求解出的R = [r1 r2 r3] 不会满足正交与归一的标准，在实际操作中，R 可以通过SVD分解实现规范化。给定 n 张棋盘格图像，每张图像有 m 个角点，最小化下述公式等同于极大似然估计：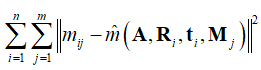

二、实验过程

2.1实验步骤

• 打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上
• 针对棋盘格拍摄若干张图片（一般10-20张）
• 在图片中检测特征点（Harris特征）
• 利用解析解估算方法计算出5个内部参数，以及6个外部参数
• 根据极大似然估计策略，设计优化目标并实现参数的refinement

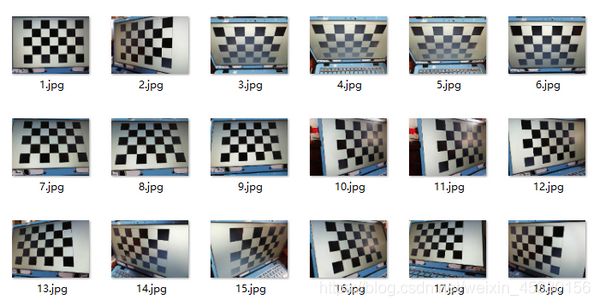
实验没有打印出照片，采用制作棋盘进行拍摄的方法，下面拍摄的照片有18张，棋盘每个小方格的边长为3cm，拍摄手机：华为8x。

2.2实现

实际应用中，常使用MATLAB标定工具箱进行相机标定 Camera Calibration Toolbox for Matlab，只需导入拍摄的棋盘格照片，输入一些参数，然后对每张照片选择棋盘区域，就可以自动完成整个标定过程，并得到可视化的标定结果。

• 打开matlab，在应用里找到“Camera Calibrator”并打开
• 在新窗口中选择添加图片“Add Images”
• 添加图片之后，设置棋盘格的实际大小（这里为30mm）
• 点击“Calibrate”开始计算

2.3实验结果

角点检测：

内参矩阵：

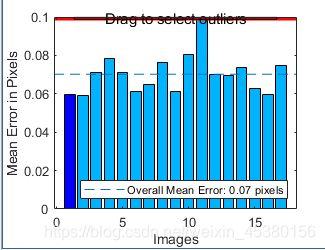
平均误差0.07：

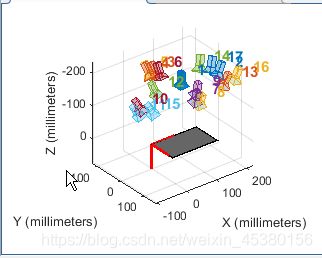
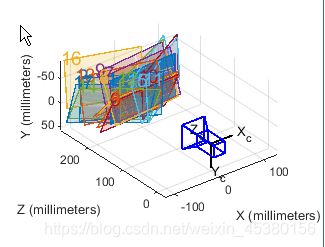
外参可视化，以棋盘格为中心（左图）和以相机为中心（右图）：

     

 

opencv计算的内参矩阵：

三、实验总结

（1）相比较Matlab标定工具箱进行标定的结果和代码实现的标定，发现两者的内参基本相同。

（2）在添加图片的时候，可能有图片拍摄得不是很好，18张图片最后标定的只有17张。在拍摄照片的时候可以尽量的拍好清楚一些，角度不要过大。

参考：

标定介绍：https://blog.csdn.net/weixin_43361953/article/details/89291696

https://blog.csdn.net/hitzijiyingcai/article/details/82715921