算法导论 | 第24章 单源最短路径
零、基础
1、单源最短路径问题:给定一个图,找到从给定源结点s,到每一个结点v的最短路径。
2、可以在这个问题上进行扩展:
①单目的地最短路径问题:找到从每个结点v到目的地t的最短路径。----将图的每个边的方向翻转,求解单源最短路径问题(这里必须要通过翻转边的方向,才能有下一步的遍历,不能简单的看从t到v的最短路径!)
②单节点对最短路径问题:找到指定结点u到指定结点v的最短路径。
③所有结点对最短路径问题:对于每一对u和v,找到从u到v的最短路径。虽然可以将每一个结点都运行一遍单源最短路径算法,但效率低;在25章中讨论更快的算法。
④最短路径的最优子结构:最短路径算法依赖于一个重要性质----两个节点之间的一条最短路径包含着其他的最短路径。
3、最短路径表示
我们不但希望计算出最短路径的长度,还需要计算最短路径上的结点。那么可以参考广度优先搜索树那样,定义一个v.p指向前驱结点的指针。当我们通过算法遍历过后,就能通过v.p来得到想要的路径。
4、松弛操作
松弛操作:对每个顶点v∈V,都设置一个属性d[v],用来描述从源点 s 到 v 的最短路径上权值的上界,成为最短路径估计(Shortest-path Estimate),同时π[v]代表前趋。
初始化
INITIALIZE-SINGLE-SOURCE(G, s)
1 for each vertex v ∈ V[G]
2 do d[v] ← ∞
3 π[v] ← NIL
4 d[s] ← 0松弛过程:当增加边(u,v)时,测试从s到v的最短路径改善。也就是比较s->v 和 s->u + s->v两者,取最小值来更新v.d信息。并且也要更新父节点指针,代码如下
RELAX(u, v, w)
1 if d[v] > d[u] + w(u, v)
2 then d[v] ← d[u] + w(u, v)
3 π[v] ← u一、Bellman-Ford算法
1、算法原理
(1)Bellman-Ford算法能在一般情况下(存在负权边的情况)下,解决单源最短路径问题。
(2)对于给定的带权有向图 G = (V, E),其源点为 s,加权函数为 w:E → R,对该图运行 Bellman-Ford 算法后可以返回一个布尔值,表明图中是否存在着一个从源点可达的权为负的回路。若存在这样的回路,问题无解;否则,算法产生最短路径及其权值。
(3) Bellman-Ford算法运用松弛技术,对每个顶点 v,逐步减小从源 s 到 v 的最短路径的权的估计值 d[v] 直至其可达到实际最短路径的权 δ(s, v) 。算法返回布尔值True,当且仅当图中不包含从源点可达的负权回路
2、算法实现
BELLMAN-FORD(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 for i ← 1 to |V[G]| – 1
3 do for each edge (u, v) ∈ E[G]
4 do RELAX(u, v, w)
5 for each edge (u, v) ∈ E[G]
6 do if d[v] > d[u] + w(u, v)
7 then return FALSE
8 return TRUE说明:
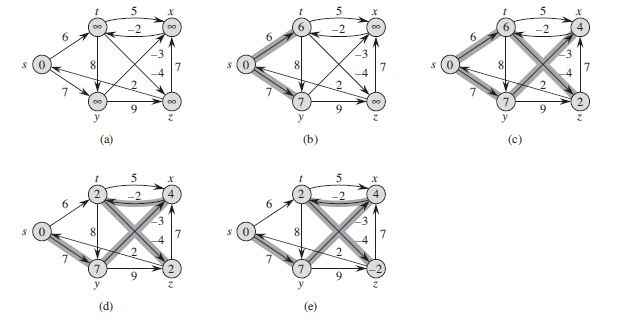
(1)该算法不是选定一个点,然后再遍历这个点发出的边,这里将边排列一定的顺序,然后按照边来遍历。
正如上图中按照(t,x),(t,y),(t,z),(x,t),(y,x),(y,z),(z,x),(z,s),(s,t),(s,y)顺序进行。
(2)最后通过d[v] > d[u] + w(u, v)来检查,因为通过v-1次遍历,已经得到了最短路径,如果还存在这种关系,证明存在负值回路。
(3)整个遍历过程进行v-1次。
考虑:为什么要循环V-1次?
答:因为最短路径肯定是个简单路径,不可能包含回路的,
如果包含回路,且回路的权值和为正的,那么去掉这个回路,可以得到更短的路径
如果回路的权值是负的,那么肯定没有解了
图有n个点,又不能有回路
所以最短路径最多n-1边
又因为每次循环,至少relax一边
所以最多n-1次就行了
3、时间复杂度
Bellman-Ford虽然很简单,但是复杂度太高,达到了O(VE),从上边图示中可以看出:(a) t,x,y,z 边的松弛是无用操作;(b) s,x,z 边的松弛是无用操作;(c) s,t,y边的松弛是无用操作;(d) s,x,y,z边的松弛是无用操作。也就是说,只有更新过的点所做的松弛才是有效操作,所以出现了更高效的算法,即SPFA:http://mindlee.net/2011/11/18/shortest-paths-algorithm/
二、有向无环图中的单源最短路径问题
1、算法原理
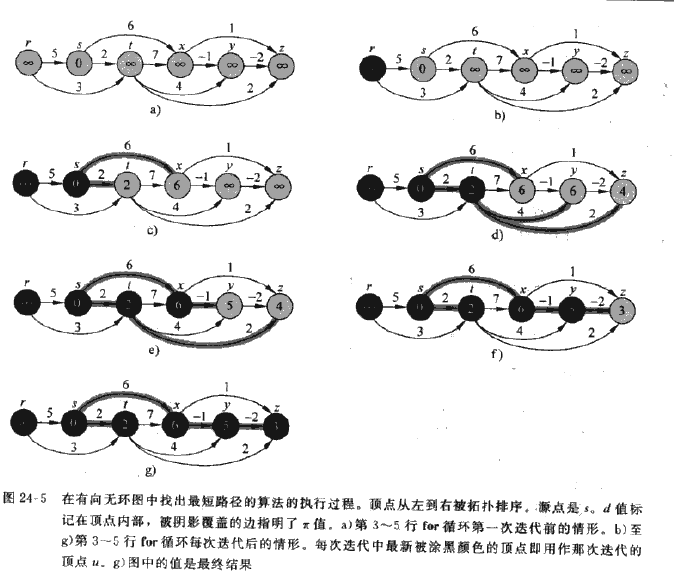
(1)根据拓扑排序对有向无环图进行松弛操作。可以得到时间复杂度为O(v+e)的算法。
(2)允许有负值的边,但不允许有回路。
2、算法实现
(1)先通过拓扑排序对图进行排序
(2)然后按照拓扑排序产生的顺序,依次遍历每个结点的出射边。并进行松弛。
(3)得到想要结果。
3、时间复杂度
时间复杂度为O(V+E)
三、迪杰斯特拉(Dijkstra)算法
基本思想
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 ... 重复该操作,直到遍历完所有顶点。
操作步骤
(1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
(2) 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
说白了,就是选取一个点S,然后更新与其相连的结点的v.d值;再选取v.d值最小的结点,再更新与其相连的v.d的值...最后得到想要的结果。当然也要维护v.p的信息!
算法图解
![]()
以上图G4为例,来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。
![]()
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
四、性能分析
1、Bellman-Ford算法
该算法在任何情况下都能用,即使包含负值回路,该算法也能“报错”。实现简单,但事件复杂度较高,达到O(VE)。
2、有向无环图中的单源最短路径问题
该算法利用拓扑排序,必须要求图中无环,不过图中可以存在权值为负数的边。时间复杂度为O(V+E).
3、迪杰斯特拉(Dijkstra)算法
要求最高,所有的权值必须非负数。但时间复杂度较低,效果较好。
该算法执行三种优先队列来维持最小优先队列。
(1)通过利用结点的编号1~|V|来维持最小优先队列(通过在数组中遍历查找最小值),时间复杂度为O(V^2)。
(2)如果是稀疏图,可以利用二叉堆来实现----- O((V+E)lgV)
(3)使用斐波那契堆来实现,可以改善到O(VlgV + E)