PCA线性代数讲解
线性代数及PCA详解
本章对最近学习的线性代数知识进行总结,最后以PCA为例运用线代中的相关知识讨论其中的原理。才疏学浅,各位有什么意见可以讨论,一起查缺补漏。
1. 线代基础
对于深度学习,它需要一定的数学和机器学习基础,特别的,线性代数、概率与信息论和数值计算尤为重要(参见《deep learning》一书)
所以我们本章主要对线代进行讨论,当然主要是为了针对PCA包含的知识点。如果有同学希望可以完整学习线代,可以戳这里。
线代主要围绕线性变换展开,其中变换指的是一种函数关系:输入输出都为向量的一种函数,但是既然取名为变换,意为强调一种运动关系;线性表示变换的约束:一为原点不能变,二为保持网格线平行且均匀分布。
而描述线性变换也很简单,通常一组线性无关向量即可,称为基。基可以理解为构建向量世界的基础,任何向量都可以利用它线性组合而成。
我们利用最多的就是i帽和j帽(即正交基(1,0),(0,1)注:一般描述为列向量,为了方便,本章的向量都为列向量)
如下图所示,α=(3,2)向量其实具体应该描述为α=3i+2j
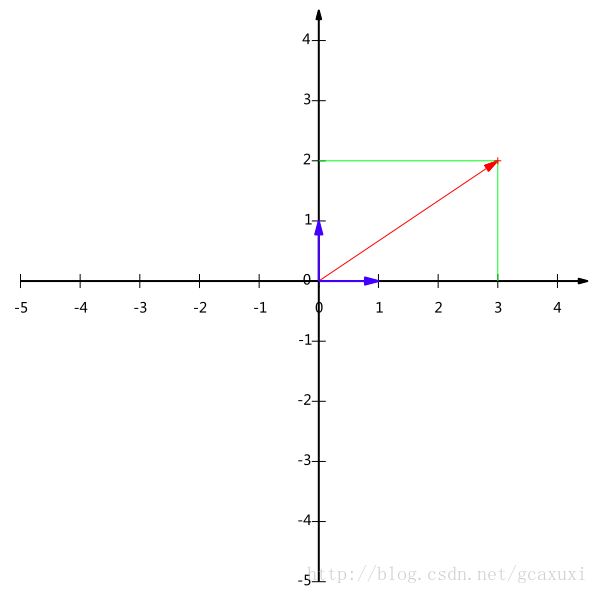
既然如此,假如我们不再使用常规的i帽和j帽最为基,例如小明同学非要换一组其他的(例如将i,j旋转90°,其实这就是一种线性变换)基,那么在他看来,原来的α该怎么描述呢?
可能有人会问,α并未变化,产生差别的原因是?在这里,我们的视角和小明的视角并不一样,更进一步说,是因为我们和小明选取的坐标(参考)系不一样。我们看到的α是在xy坐标系下3倍i帽与2倍j帽的线性组合,而小明看到的是旋转后的坐标系,这时我们需要利用小明选取的基来描述α。
具体说来,可以有两种方法求解“小明眼中α的坐标”:
- 将α投影到新基上,得出投影长度(有方向,即可正负)即为坐标;
- 通过坐标变换公式求得
先说方法一,先说明一下投影的含义,一方面,从几何意义上,如下图所示,即将向量向另一向量所在直线做垂线,则投影长度即为蓝色向量与垂线交点的向量长度;另一方面,内积与投影关系密切,有A·B=|A|cos(a)|B|,这里设A为投影向量,则B为被投影向量,则|A|cos(a)为投影矢量长度,|B|为被投影向量的模。再进一步,如果我们假设B的模为1,即让|B|=1,那么就变成了:A·B=|A|cos(a)
简而言之,如果设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度!
继续说下面这幅图,图中基由(1,0),(0,1)转换为(1/√2,1/√2),(-1/√2,1/√2)
注:这里基的坐标都是以我们视角的坐标系来看的
那么,新基坐标系下,α的坐标计算为:
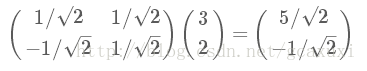
即下图所示:
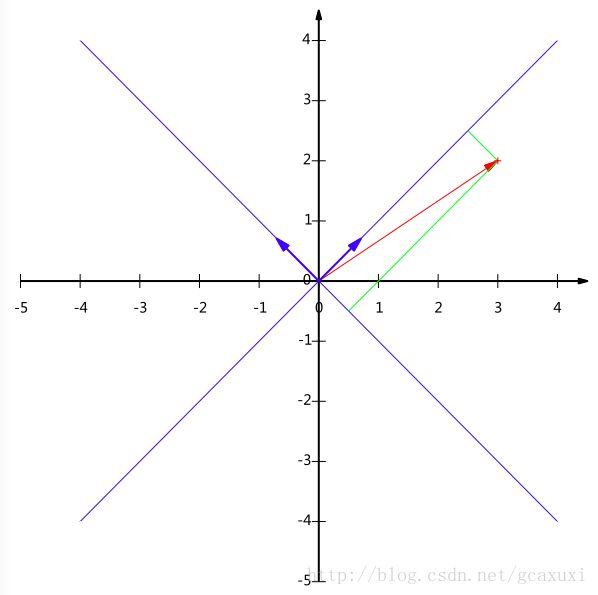
一般说来,如果我们有M个N维向量,想将其变换为由R个N维向量表示的新空间中,那么首先将R个基按行组成矩阵A(上例中我们把基(1/√2,1/√2),(-1/√2,1/√2)按行排列),然后将向量按列组成矩阵B,那么两矩阵的乘积AB就是变换结果,其中AB的第m列为A中第m列变换后的结果。
简单表达:B`X=Y ①(等式左边,前者为B 的转置,后者为转换前坐标,二者均为同一坐标系下;Y为转换后的坐标,即为小明眼中新基下的坐标)
最后,上述分析同时给矩阵相乘找到了一种物理解释:两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。
接下里说说方法二,在介绍坐标变换之前,先说明一下基变换。如同方法一所说的,由旧基到新基,其实经历了一个变换,这个变换的桥梁我们称之为过渡矩阵。数学表达为:B=AP,B为新基组成的集合(矩阵),A为旧基组成的集合,P为过渡矩阵。
则有,P逆 X=Y ②(特殊的,如果A为标准单位正交基,即(1,0),(0,1)列向量组成的单位矩阵E,则此时B=P,所以P逆 = B逆,②式变为B逆 X=Y ,另外因为B为正交基,B`=B逆,所以②式还可以变为B转置 X=Y 或者P转置 X=Y )
综上,总结一下,我们主要讲了基变换下的坐标变换,涉及投影、内积等知识,最重要的X与Y之间的转换:B`X=Y ①P逆 X=Y ②
这些都是接下来我们讨论PCA的基础,试想一下,投影的几何示意是不是有种降维的味道在里面?具体而言,假设我们有多个二维数据,我们将其降为一维,可能的做法是将这些点投影到某一轴上。接下来的问题就是,如何选择这个轴,我们采用概率和特征值等知识来解释选择的合理性。
2.PCA
我们这里首先说明我们的目标,然后讨论将会采取的策略,最后说说来达到目的的一些方法。
2.1定义
PCA(Principal Component Analysis):通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。
2.2动机
这里我们采用网络张洋《PCA的数学原理》文中的例子,某个淘宝店2012年全年的流量及交易情况可以看成一组记录的集合,其中每一天的数据是一条记录,格式如下:
(日期, 浏览量, 访客数, 下单数, 成交数, 成交金额)
其中“日期”是一个记录标志而非度量值,而数据挖掘关心的大多是度量值,因此如果我们忽略日期这个字段后,我们得到一组记录,每条记录可以被表示为一个五维向量,其中一条看起来大约是这个样子:
(500,240,25,13,2312.15)T
继续强调这里,用了转置,因为习惯上使用列向量表示一条记录(后面会看到原因),本文后面也会遵循这个准则。不过为了方便有时会省略转置符号,但我们说到向量默认都是指列向量。
从经验我们可以知道,“浏览量”和“访客数”往往具有较强的相关关系,而“下单数”和“成交数”也具有较强的相关关系。这里我们非正式的使用“相关关系”这个词,可以直观理解为“当某一天这个店铺的浏览量较高(或较低)时,我们应该很大程度上认为这天的访客数也较高(或较低)”。后面的章节中我们会给出相关性的严格数学定义。
这种情况表明,如果我们删除浏览量或访客数其中一个指标,我们应该期待并不会丢失太多信息。因此我们可以删除一个,以降低机器学习算法的复杂度。
但是凭借经验,可能选择的标准不够精准:我们到底删除哪一列损失的信息才最小?亦或根本不是单纯删除几列,而是通过某些变换将原始数据变为更少的列但又使得丢失的信息最小?到底如何度量丢失信息的多少?如何根据原始数据决定具体的降维操作步骤?
PCA作为解决此类的问题的关键登场了。
2.3目的
根据上述的经验,我们认为让数据进行合理的降维,一是尽量减少信息的缺失,即保全信息的所有内容;二是减少数据之间的相关性(例子中有所体现)。
从统计上来说(另一层面是从概率上来说),方差体现着离散程度,直观而言,二维数据降为一维,这个问题实际上是要在二维平面中选择一个方向,将所有数据都投影到这个方向所在直线上,用投影值表示原始记录。
那么如何选择这个方向(或者说基)才能尽量保留最多的原始信息呢?我们希望投影后的投影值尽可能分散。也就是方差尽可能的大。
- 统计中另一指标协方差,其用于衡量两个变量的总体误差,直接理解为相关性即可(由其得到的相关系数可能更为直接)。
我们希望的是协方差尽可能的小,如果为0,则可以得出目标变量之间不相关(或者成为线性独立,不相关是指两个随机变量没有近似的线性关系,而独立是指两个变量没有任何关系。)
由上述1,2,可以得到我们的目的:数据之间的1.方差尽可能的大,2.协方差逼近0
2.4策略
这里我们假设数据每一维度特征的均值为0(我们有能力达到这样的效果,可以称之为0均值化,当然也可以不这样做),上述的方差和协方差公式为:
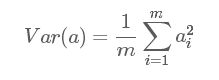
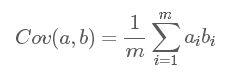
假设我们只有a和b两个字段,那么我们将它们按行组成矩阵X(这里和上面第1节内容定义不一样,每一列代表一个样本或者一条记录):
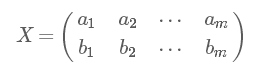
然后我们用X乘以X的转置,并乘上系数1/m:
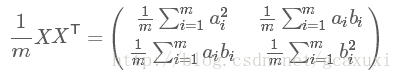
这个矩阵对角线上的两个元素分别是两个字段的方差,而其它元素是a和b的协方差。两者被统一到了一个矩阵的。
根据矩阵相乘的运算法则,这个结论很容易被推广到一般情况:
设我们有m个n维数据记录,将其按列排成n乘m的矩阵X,设C=X乘以X的转置,并乘上系数1/m,则C是一个对称矩阵,其对角线分别个各个字段的方差,而第i行j列和j行i列元素相同,表示i和j两个字段的协方差。
2.3节知我们的目的:数据之间的1.方差尽可能的大,2.协方差逼近0,在协方差矩阵C体现就为对角元尽可能大,非对角元为0这样的数值体现。
2.5方法
上节我们得知,我们需要让协方差矩阵C体现就为对角元尽可能大,非对角元为0,有什么方法能做到这点?
特征值法
对角元尽可能大,非对角元为0 这样的描述直接的想法就是对角矩阵,那么我们能不能联系特征向量、特征值这些知识?当然是肯定的,还记得C必为对称矩阵的这一特点吗?在线性代数上,实对称矩阵有一系列非常好的性质:
1)对称矩阵特征值为实数。
2)实对称矩阵不同特征值对应的特征向量必然正交。
3)设特征向量λλ重数为r,则必然存在r个线性无关的特征向量对应于λλ,因此可以将这r个特征向量单位正交化。
···
那么我们的想法就很自然了,原数据矩阵X,由它得到协方差矩阵C,我们希望X经过变换矩阵P得到降维矩阵Y,而Y协方差矩阵为对角矩阵,这样满足了上述目的。拆分上面的语言,
“X经过变换矩阵P得到降维矩阵Y”,数学上表达为:PX=Y(XP=Y也可以,只不过二者的P不一样);
“Y协方差矩阵为对角矩阵”,设Y的协方差矩阵为D,我们推导一下D与C的关系:

目标进一步明确,我们要求变换矩阵P,P是体现我们整个线性变化的关键。我们可以通过对它的修改来达到降维这一目的。问题是P怎么求得?
我们从特征变换考虑D与C之间的关系:
假设C求得特征向量,为e1,e2,⋯,en,我们将其按列组成矩阵:
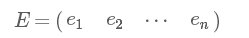
将C对角化:

很自然,我们希望Λ =D,则P =E转置P是协方差矩阵的特征向量单位化后按行排列出的矩阵,其中每一行都是C的一个特征向量。如果设P按照Λ中特征值的从大到小,将特征向量从上到下排列,则用P的前K行组成的矩阵乘以原始数据矩阵X,就得到了我们需要的降维后的数据矩阵Y。
至于K的选择,一般说来采用一定的比例作为标准(参见西瓜书p231,其中的说法是重构阈值。简单而言,就是选取的K个特征值之和占总体特征值之和的比例必须达到一定的比例)
总结一下,特征值法的算法为( 设有m条n维数据):
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵C
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
奇异值法
在实践中,我们一般不采用特征变换(evd),而是转为稳定的奇异值法(svd,稳定一说听某一老师的说法)。
SVD简单就是原矩阵A分解如下(不介绍如何推导):
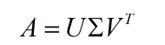
这里的U我们称为左奇异向量,对应的,VT称为右奇异向量,中间的∑是由了0块和奇异值对角块组成的矩阵。简单而言,奇异值针对于非方阵的分解,其用处很多,并不限于(PCA),直接的,还有M-P伪逆和数据压缩等用处。
对于数据压缩,SVD是很直接,分解完U,∑,V这三者可以近似还原原矩阵达到降维;需要注意的是,之前我联系奇异值法和特征值法的时候,总是以为二者可以转换,其实在EVD处理PCA时,我们进行特征转换的对象是C,其中C必为方阵(或者更进一步,C为对称矩阵);而SVD处理PCA的时候,我们处理的是原数据矩阵X,二者其实处理的对象并不一样。
对于SVD,数学知识包含内容很多,如有机会,后面我会详细研究谈论。这里我们只是针对实际PCA的工作进行应用。
对于PCA,参看2.5节,我们的目标是求得转换矩阵P
实际中,我们可以采用matlab的函数分解原数据矩阵X(重复一遍,X的一列代表一条记录或者样本,一行代表所有特征或者属性),得到U,∑,V。而这里我们可以选取U或者V作为P的选择,则我们可以进行两方面的压缩:如果选择P=U,则对行进行压缩,常规的我们可以称之为降低维度,那么和特征值法无异;如果选择P=V(此时P为右乘),则对列进行压缩,可以理解为,将一些相似的样本合并在一起,或者将一些没有太大价值的样本去掉。
可以看出,其实PCA几乎可以说是对SVD的一个包装,如果我们实现了SVD,那也就实现了PCA了,而且更好的地方是,有了SVD,我们就可以得到两个方向的PCA,如果我们对A’A进行特征值的分解,只能得到一个方向的PCA。