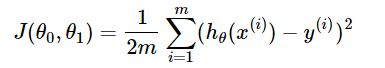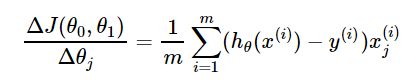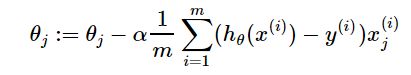深度学习基础（二）：梯度下降法GD

目录

1、前言

2、梯度下降（GD，gradient descent）

3、实验

4、代码

5、参考资料

---

1、前言

       PyTorch 能在短时间内被众多研究人员和工程师接受并推崇是因为其有着诸多优点，如采用 Python 语言、动态图机制、网络构建灵活等。 因此， 走上学习 PyTorch 的道路已刻不容缓。对于一个深度学习任务而言，通常的处理流程是：采集数据并清洗数据集，构造数据集，数据预处理、数据增强；选择模型，定义模型，确认损失函数和优化器，训练模型（权值初始化、模型微调），使用可视化工具对数据、模型、目标函数和分类结果等内容进行监控、诊断和优化。其中，确定优化器是件至关重要的事情，优化器的选择关乎我们如何选择权值初始化的方法。深度学习之所以能够取得重大成就，函数的可微是关键，可微分意味着梯度存在，可以优化求解。在PyTorch 提供了基于梯度下降法的十种优化器：SGD、 ASGD、 Rprop、RMSprop、 Adam 等。

2、梯度下降（GD，gradient descent）

      算法原理：运用损失函数的梯度更新待求参数，确认损失函数最小处对应待求参数为最优参数，实质为迭代优化算法。

      梯度下降思想的三要素：出发点、下降方向、下降步长。

      1）批量梯度下降法BGD(Batch Gradient Descent)：

           参与更新的数据：每一次迭代时使用所有样本来进行梯度的更新。

           优点：所有样本参与更新梯度，优化方向更加准确。

           缺点：样本量较大，优化速度较慢。

      2）小批量梯度下降法MBGD（mini-batch Gradient Descent）：

           参与更新的数据：每次迭代使用batchsize个样本进行参数更新，该方法是深度学习中常用的方法。

           优点：提高了内存的利用率，权衡了优化速度和准确度。

           缺点：batchsize对训练结果影响较大，需要选择合适的参数。

      3）随机梯度下降法SGD（stochastic gradient descent）

           参与更新的数据：每次迭代使用一个样本来对参数进行更新。

           优点：由于每一个样本直接参与改变梯度，参数的更新速度更快。

           缺点：由于单个样本并不能代表全体样本，优化结果容易陷入局部最小。

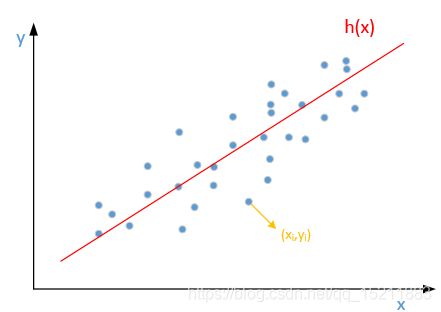
以一次函数为例推导BGD

 待求的模型：

优化目标函数：

 梯度（目标函数求偏导）：

 其中， i=1,2,...,mi=1,2,...,m 表示样本数， j=0，1 表示待求参数数量，这里为 ,。

每次迭代待优化参数的更新公式：

 其中，α为学习步长（学习率）。

3、实验

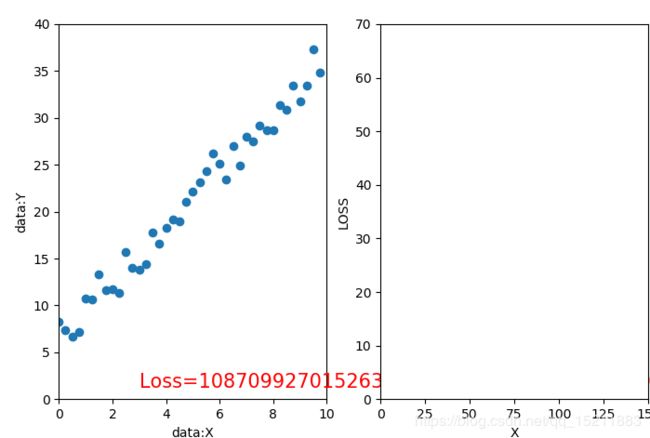
   数据： 随机数符合的线型模型： y=3*x+4+5*np.random.rand(40)

1、迭代次数

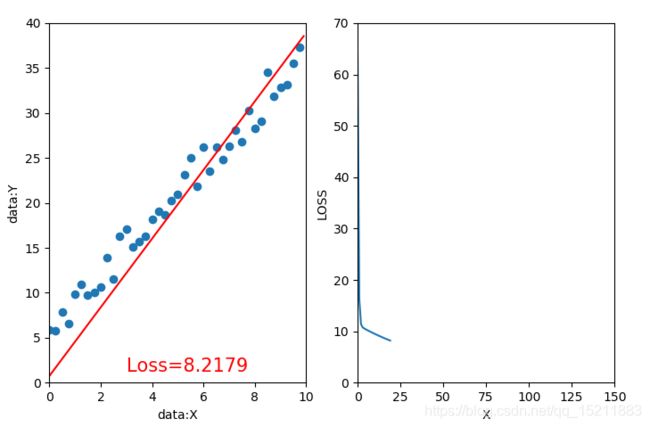
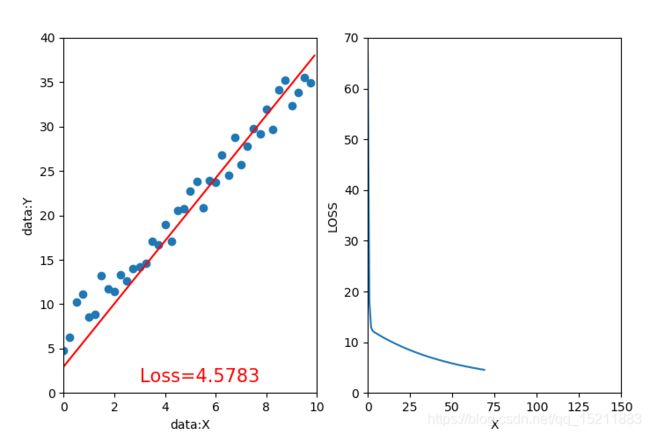
     1.1、迭代20次，学习率=0.02，初始值w=0,b=-1          1.2、迭代70次，学习率=0.02，初始值w=0,b=-1

2、初始权值 (w,b)

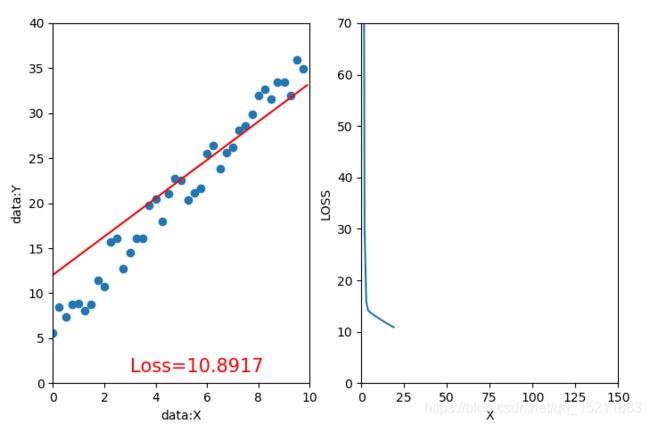
     2.1、迭代20次，学习率=0.02，初始值w=-1,b=0         2.2、迭代20次，学习率=0.02，初始值w=-20,b=10  

3、学习率

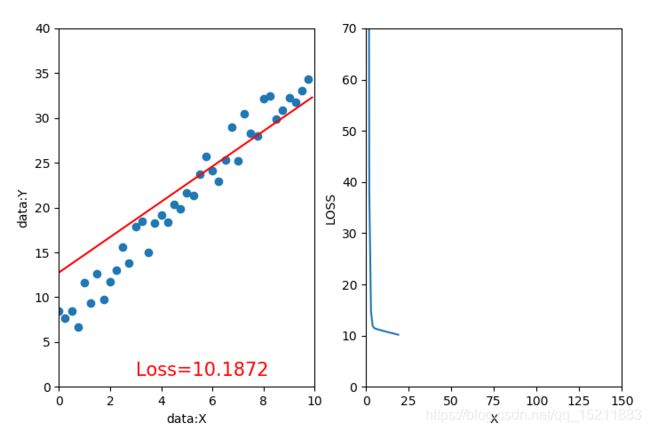
   3.1、迭代20次，学习率=0.01，初始值w=-20,b=10        3.2、迭代20次，学习率=0.1，初始值w=-20,b=10 。

4、小结

   1、在深度学习中初始化参数十分重要，良好的初始化能让模型快速收敛，而糟糕的初始化可能会导致模型迅速崩溃，如3.2。

    2、初始值w=-1,b=0比w=-20,b=10离最优值w=3,b=5距离更近，在训练过程中相同迭代次数，损失函数（误差函数）更小，这意味着优化速度更快。

    3、学习率应当设置成一个很小的数值，学习率过大容易带来优化风险，不收敛或陷入局部最小值。

4、代码

# -*- coding: utf-8 -*-
"""
Created on Fri Jul 26 10:14:38 2019
批量梯度下降法（BGD）
@author: xiaoxiaoke 
"""
import numpy as np
import matplotlib.pyplot as plt

def computeLossErrorAllpoints(w,b,points):
    totalError=0
    for i in range(0,len(points)):
        x=points[i,0]
        y=points[i,1]
        totalError+=(w*x+b-y)**2
    return totalError/float(len(points))

def stepGradient(wCurrent,bCurrent,points,learnRate):
    w_gradient_loss=0
    b_gradient_loss=0
    for i in range(0,len(points)):
        w_gradient_loss+=-(2/float(len(points)))*(points[i,1]-(wCurrent*points[i,0]+bCurrent))*points[i,0]
        b_gradient_loss+=-(2/float(len(points)))*(points[i,1]-(wCurrent*points[i,0]+bCurrent))
        
    w_new=wCurrent-learnRate*w_gradient_loss
    b_new=bCurrent-learnRate*b_gradient_loss
    return [w_new,b_new]

def generateRandomData(numSum):
    x=np.arange(0,10,0.25)
    y=3*x+4+5*np.random.rand(40)
    points=np.vstack((x,y))
    points=points.transpose()
    return points

if __name__ == '__main__':
   points= generateRandomData(100)
   wCurrent=-20
   bCurrent=10
   LossArray=[]
   plt.figure
   for i in range(0,20):
      wCurrent,bCurrent=stepGradient(wCurrent,bCurrent,points,0.1) 
      lossError=computeLossErrorAllpoints(wCurrent,bCurrent,points)
      x=np.arange(0,10,0.1)
      y=wCurrent*x+bCurrent
      
      plt.subplot(121)
      plt.cla()
      plt.scatter(points[:,0],points[:,1])
      plt.plot(x,y,'r')
      plt.xlabel("data:X")
      plt.ylabel("data:Y")
      plt.xlim((0,10))
      plt.ylim((0,40))
      plt.text(3, 1.2,'Loss=%.4f' %lossError,fontdict={'size':15, 'color':'red'})
      plt.pause(0.1)
      
      LossArray.append(lossError) 
      plt.subplot(122)
      plt.cla()
      xLossArray=np.arange(0,len(LossArray),1)
      plt.plot(xLossArray,LossArray)
      plt.xlabel("X")
      plt.ylabel("LOSS")
      plt.xlim((0,150))
      plt.ylim((0,70))
      plt.pause(0.01) 
       
      print(i,wCurrent,bCurrent,lossError)     

5、参考资料

1、PyTorch 模型训练实用教程

2、https://blog.csdn.net/u012759136/article/details/52302426

3、https://baijiahao.baidu.com/s?id=1613121229156499765&wfr=spider&for=pc

4、https://www.cnblogs.com/maybe2030/p/5089753.html