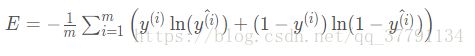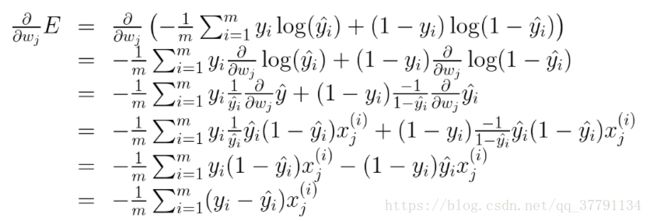7天深度学习-day3-梯度下降
1、梯度下降实现
我们了解到为了最小化误差函数,我们需要获得一些导数。我们开始计算误差函数的导数吧。首先要注意的是 s 型函数具有很完美的导数。即
σ′(x)=σ(x)(1−σ(x))
原因是,我们可以使用商式计算它:
现在,如果有 m个样本点,标为 x^(1), x^(2), ......, x^(m),, 误差公式是:
我们的目标是计算 E,E, 在单个样本点 x 时的梯度(偏导数),其中 x 包含 n 个特征,即x = ![]()
类似的计算将得出:
总之
如果思考下,会发现很神奇。梯度实际上是标量乘以点的坐标!什么是标量?也就是标签和预测直接的差别。这意味着,如果标签与预测接近(表示点分类正确),该梯度将很小,如果标签与预测差别很大(表示点分类错误),那么此梯度将很大。请记下:小的梯度表示我们将稍微修改下坐标,大的梯度表示我们将大幅度修改坐标。
如果觉得这听起来像感知器算法,其实并非偶然性!稍后我们将详细了解。
感知器算法:
感知器算法:《李航:统计学习方法》--- 感知机算法原理与实现 https://blog.csdn.net/u013358387/article/details/53303932
2、梯度下降算法推到与实现
两者还是有区别的
3、Logistic(对数概率)感知器和梯度下降。
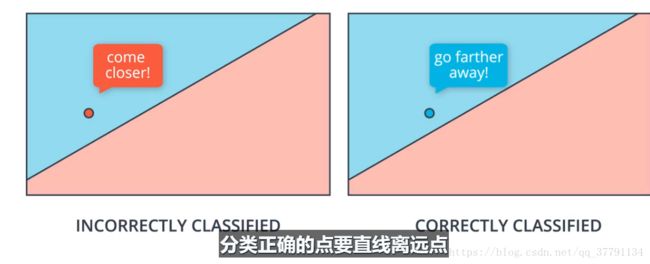
感知器不是对所有的点都进行权值和偏差改变,而是对待错误分类的值,但是梯度下降算法则是对所有的点都进行权值更新,(错误的点会说直线离我近点,正确的点说直线离我远点)
两者的对比,仔细看是一样的。 i表示的是x的第i个特征。
感知器(perceptron)算法与梯度下降(gradient descent)算法的区别:
1.在感知器算法中,并非每个点都会更改权重,只有分类错误的点才会
2.在感知器算法中,y hat只能是1或者0;而在梯度下降算法中,y hat 可以是0到1之间的值
3.在梯度下降算法中,一次预测被正确分类的点会更改权重,让分类直线离这个点远点,而分类错误的点也会更改权重,让分类直线离这个点更近些
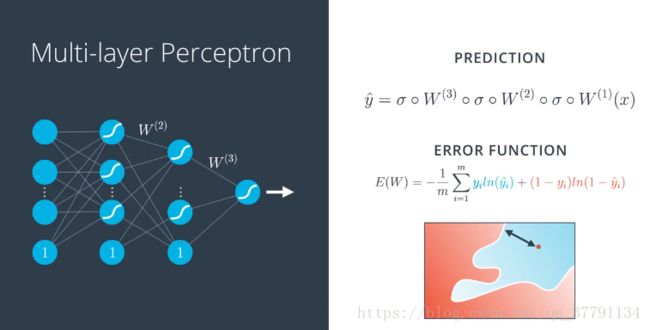
4、神经网络结构
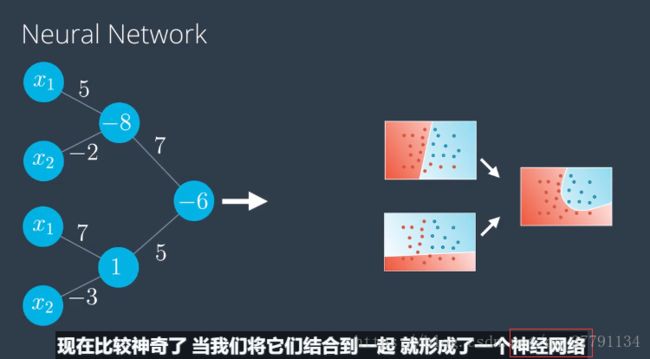
现在可以将这些构建基石组合到一起了,并构建出色的神经网络!(或者你愿意,也可以叫做多层级感知器。)
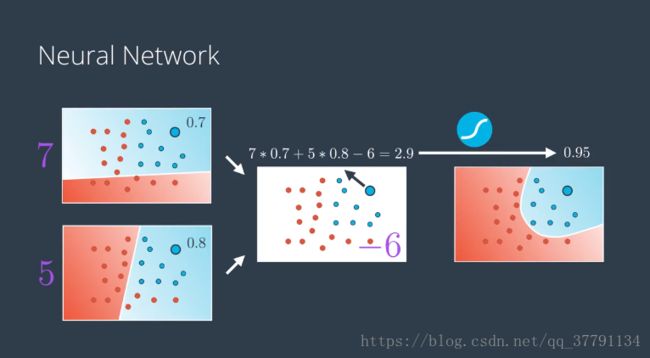
演示如何将两个感知器组合成第三个更复杂的感知器
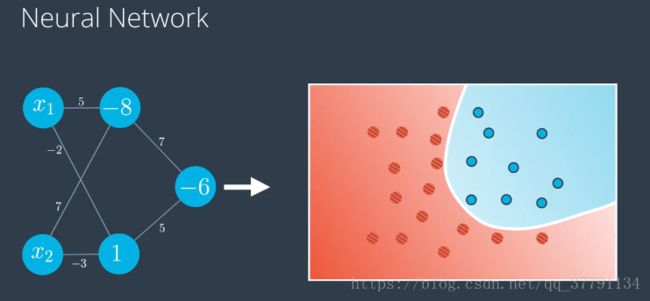
之前我们有一条直线,它是输入值审议权重加上偏差的线性组合,现在的模型是两个之前的模型乘上权重再加上某个偏差的线性组合,所以就想是右边的模型是两个之前的线性模型的线性组合,甚至可以看成成是两个模型之前的一条曲线,这不是巧合,这就是构建神经网络的核心。我们如何构建神经网络:对现有的线性模型进行线性组合,得到更加复杂的新模型。
看下面一组示例图我想会更加清楚些:
左侧的权重告诉我们线性模型具有的方程、两个模型的线性组合是多少。以便获得右侧的曲线非线性模型。
看到左边的神经网络时,请思考下改神经网络定义的非线性界线是什么?
左边是图标使用的记法是把偏差放在节点里面,右边是把偏差从感知器里单独拿出来做节点,是在每层中独有一个来自其中是1的节点的偏差单位,如顶部节点的-8,变成来自偏差节点的标为-8的边,这个神经网络使用的是sigmoid激活函数。
多层级
并非所有神经网络都看起像上面的那样。可能会复杂的多!尤其是,我们可以执行以下操作:
- 向输入、隐藏和输出层添加更多节点。
- 添加更多层级。
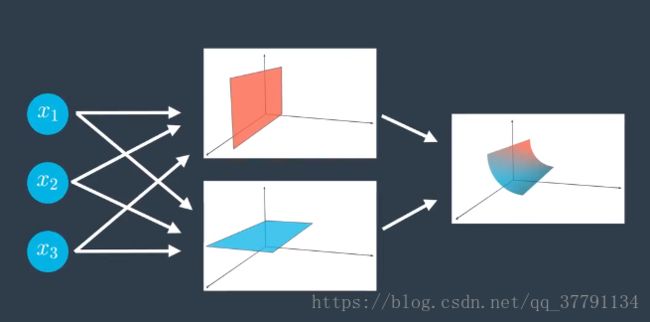
对三个线性模型进行组合
输入层有更多的节点呢?不再处在二维空间,处在三维空间。
输出层有更多节点嗯?这就是具有多种类的分类模型
例如:无人驾驶、游戏中的电脑玩家,都具有非常非常多的隐藏层,神经网络使用高度非线性化的边界,拆分整个n维空间
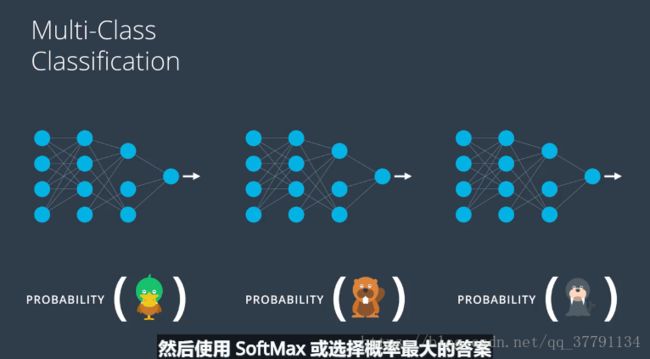
多类别分类
现在我们详细讲解下如果神经网络需要对超过一个输出的数据进行建模,我们该如何操作。
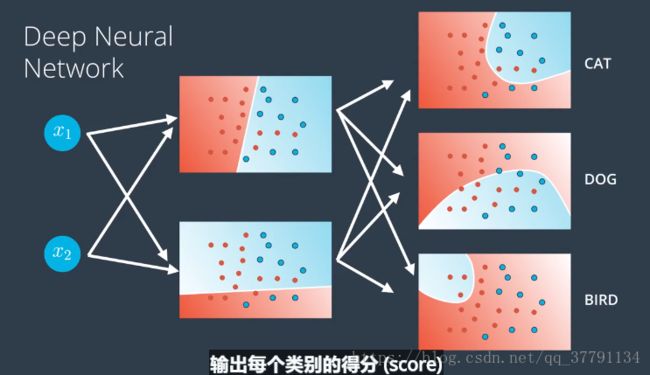
如果有下图办法就有点杀鸡用牛刀
我们应该这么做,神经网络第一层级应该足以描述图片内容,只需要最后一个层级告诉我们图片中是哪个动物
实际上我们也是这么做的,我们要做的是在输出层添加更多节点
我们得到的得分(score)并使用之前定义的softMax函数,得到所需的每种类别的概率。以上就是神经网络进行多分类的方法。
5、前向反馈
前向反馈是神经网络用来将输入变成输出的流程。我们仔细研究下这一概念,然后详细了解如何训练网络。我们已经定义了什么是神经网络,我们需要知道怎么训练他们,训练他们实际上就是各边的权重应该是多少,这样才能很好地对数据建模。为 学习如何训练他们的,我们需要仔细研究,他们如何处理输入来获得输出结果的。
我们看出这个模型不好,依据第三个坐标,y是1。
如果我们有更负责的神经网络,是一样的,粗边对应的是大的权重,细边对应的是大的权重,神经网络在上下图中都标出了这个点,得到的结果是顶部模型的小数字,那么这个位于红色区域的点是蓝色的概率很小,从得到个模型得出一个大的数字,点在蓝色区域,它是蓝色的概率很大,这两个模型结合成这个非线性模型,输出层绘出这个点,告诉我们是蓝色的概率,可看出这个模型不好,因为它将点绘在红色区域,但点是蓝色,,这个流程叫做前向反馈。
如何将第一层级的线性模型着成第二层级的非线性模型,需要一些数学知识,y*是预测,即点标为蓝色的概率,这就是神经网络的作用,他们传入输入向量,应用线性模型序列和s型函数,这些地图相结合,变成高度非线性地图
要计算预测y*,我们从单位向量x出发,然后应用第一个矩阵和s型函数,得到第二层级的值,然后应用的第二个矩阵和另一个s型函数,得到第三层级的值,以此类推,直到得到最终预测y*。这就是神经网络从输入向量中,获得预测用到的前向反馈流程。
误差函数
和之前一样,神经网络将产生误差函数,最终我们需要最小化该误差函数。下面的视频演示了神经网络的误差函数。
但是这个函数依然可以高斯我们点分类错误的程度有多大,但是现在我们看到的是更复杂的界限。
反向传播
现在,我们准备好训练神经网络了。为此,我们将使用一种方法,叫做反向传播。简而言之,反向传播将包括:
- 进行前向反馈运算。
- 将模型的输出与期望的输出进行比较。
- 计算误差。
- 向后运行前向反馈运算(反向传播),将误差分散到每个权重上。
- 更新权重,并获得更好的模型。
- 继续此流程,直到获得很好的模型。
从概念上解释什么是反向传播 ,就是问每个模型你想要自己怎么变化,然后改变权重,使得结果接近预期值。
反向传播数学
后面的几个视频将深入讲解数学知识。如果不想听也没有关系,现有的很多代码库和深度学习框架比如 Keras,能够很好并且很简单地完成这个任务。如果你想立即开始训练网络,请转到下个部分。但是如果你喜欢计算各种导数,那么我们深入了解下吧!
输入先经过一个线性方程 再经过s函数,下面误差公式,它是所有点的平均结果,蓝色项和红色项分别代表蓝色和红点,为了从误差之巅上下来,我们需要计算梯度,梯度是误差函数关于权重(从w1到wn)和偏差的偏导数所形成的的向量,他们所对应是这些边。
在多层感知器中该如何进行反向传播呢?情况稍微复杂些,但本质上几乎一样。这是我们预期的结果,其实就是一些复合函数 包括矩阵乘法和s函数,误差函数几乎保持不变,只是y*变复杂了,梯度几一样,只是表达式长了很多,是一个很大的向量,每一项分别是误差函数关于每个权重的偏导数,这些项对应所有的边,如果严谨点,就是下面的图啦。
预期结果是s函数和矩阵乘法的复合,梯度有所有这些偏导数组成,这里看上去是矩阵,实际上 是个很长的向量,梯度下降将进行下面的的步骤:拿出每个权重wij(k),我们对其更新,加上 一个数字(学习速率)乘以E相对于该权重的偏导数。将得到更新后的权重wij’(k),于是得到了一个全新的模型、包含了新的权重,可以对点进行更加准备的分类。
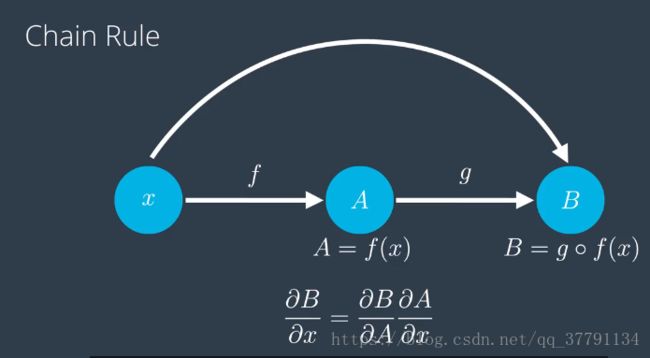
链式法则
我们需要复习下链式法则,以便计算导数,这个对复合函数的求导法则,对我们很有帮助,以为你前向反馈急速多种函数的复合。
w(1)是第一层级对应的矩阵,w(2)是第二层级对应的矩阵,预测y*是w(2)的s型函数与w(1)s型函数相结合,应用到输入x上,这就是前向反馈。
* 反向传播正好是前向反馈的逆过程 *
使用链式法则计算这些误差函数相对于标签中每个权重的导数,我能的误差函数是这杨的函数,即预测函数y*,但是预测是所有权重wij的函数,那么误差函数可以看做所有wij的函数,因此梯度是误函数E,相对于每个权重的偏导数形式的向量,我们计算下E相对于w11(1)的导数,因为y*是函数组合来的,所以自然想到了链式法则,这一部分的导师就是所有偏导数的积,故导数为:
E相对于y*的导数 × y*相对于h的导数 × h相对于h1的导数 × h1相对于w11的导师
为了简单起见,我们只看一个感知器,对h1 、h2 、偏差单位对应的1 应用s型函数和线性方程后,得到h,则h相对于h1的导数是多少呢?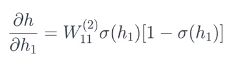 ,
,![]() 的导数正好是:
的导数正好是:![]()
计算 sigmoid 函数的导数
回想一下,sigmoid 函数有一个美丽的导数,我们可以在下面的计算中看到。这将使我们的反向传播步骤更加简洁。
神经网络就是这么训练的!
7、实验部分 分析学生数据
现在,我们已经准备好将神经网络用于实践。 我们将分析以下加州大学洛杉矶分校的学生录取的数据。
在这个 notebook 中,你将执行神经网络训练的一些步骤,即:
- One-hot 编码数据
- 缩放数据
- 编写反向传播步骤
https://blog.csdn.net/zzulp/article/details/79318108 这个也是吴恩达老师的深度学习笔记,可以参考