在单源路径问题中常涉及到松弛技术(Relaxation),其原理如下:


Bellman-Ford 算法
该算法主要是解决边的权重可能为负的情况。
伪代码如下:

EG:

运行时间:O(VE)。
Bellman-Ford 算法的一个重要应用是差分约束(Difference and Constraints),其原理如下:
对于一个差分约束Ax

有像无循环图中的单源路径
伪代码:

EG:

运行时间:O(V+E)。
Dijkstra 算法
伪代码:

EG:

运行时间:

若用数组存储,则 T=O(V²)
若用二项式堆存储,则T=O((V+E)lgV)
若用斐波拉契堆存储,则T=O(E+VlgV)
===============================================================================================================================
Bellman-Ford算法完整代码:
#include
#include
using namespace std;
typedef char vType;
typedef struct edge{
vType vs;
vType ve;
int weight;
}edge;
typedef struct gVertex{
vType key;
vType parent; //the parent of this node
int d; //discovered time
}gVertex;
typedef struct gEdge{
gVertex *u;
gVertex *v;
int w;
}gEdge;
typedef struct Graph{
int vNum;
int eNum;
gVertex *V;
gEdge *E;
int kind; //the type of the Graph
}Graph;
void Graph_Init(Graph &G,vType *V,edge *E,int vNum,int eNum)
{
G.vNum = vNum;
G.eNum = eNum;
G.V = new gVertex[G.vNum];
G.E = new gEdge[G.eNum];
for(int i=0; ikey = E[i].vs;
eNode->key = E[i].ve;
G.E[i].u = sNode;
G.E[i].v = eNode;
G.E[i].w = E[i].weight;
}
}
int Locate(Graph &G,vType s)
{
for(int i=0; id or u->d + w >= INF,it will overflow
if(u->d == INT_MAX || u->d + w >= INT_MAX)
return ;
if(v->d > u->d + w){
v->d = u->d + w;
v->parent = u->key;
}
}
int Graph_BellmanFord(Graph &G,vType s){
Init_SingleSource(G,s);
//swap the starting node with the first node in G.V
int s_i=Locate(G,s);
gVertex *temp = new gVertex();
*temp = G.V[s_i];
G.V[s_i]=G.V[0];
G.V[0] = *temp;
//for every node,relax eNum edges
for(int i=1; ikey);
int v_j = Locate(G,(G.E[j].v)->key);
gVertex *uNode = &G.V[u_j];
gVertex *vNode = &G.V[v_j];
Graph_edgeRelax(uNode,vNode,G.E[j].w);
}
cout<<"Every round:"<key);
int v_j = Locate(G,(G.E[j].v)->key);
gVertex *uNode = &G.V[u_j];
gVertex *vNode = &G.V[v_j];
cout<<"uNode->d="<d<<" vNode->d="<d<<" w="<d > uNode->d + G.E[j].w)
return -1;
}
return 1;
}
int main()
{
vType V[]={'s','t','y','x','z'};
edge E[]={{'s','t',6},{'s','y',7},{'t','y',8},{'t','x',5},
{'t','z',-4},{'y','x',-3},{'y','z',9},{'x','t',-2},
{'z','x',7},{'z','s',2}
};
int vNum = sizeof(V)/sizeof(vType);
int eNum = sizeof(E)/sizeof(edge) ;
Graph G;
Graph_Init(G,V,E,vNum,eNum);
vType s;
cout<<"Please input the starting position:";
cin>>s;
if(Graph_BellmanFord(G,s)==1)
{
cout<<"The shortest-paths tree is:"<
运行结果:
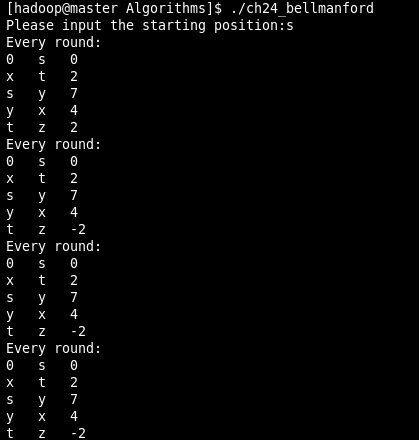

DAG 单源最短路径完整代码:
#include
#include
#include
#include
#include
using namespace std;
#define UDG 0
#define DG 1
#define WHITE 0
#define GRAY 1
#define BLACK 2
#define NONE 0
#define TREE 1
#define BACK 2
#define FORWARD 3
#define CROSS 4
typedef char vType;
typedef struct gEdge{
vType adjVertex; //the adjacency vertex pointed by this edge.
int weight; //the weight of this edge
int type; //the type of edge
gEdge *nextEdge; //Point to the next edge
}gEdge;
typedef struct gVertex{
vType key; // the key of the vertex
int color;
int d,f; // the discovered time and the finished time
vType parent; // the parent node's key after searching
gEdge *firstEdge; // point to the first edge attached to the vertex;
}gVertex;
typedef struct ALGraph{
int vNum;
int eNum;
int kind; //the kind of Graph
gVertex *HeadVertex;
}ALGraph;
typedef struct edge{
vType start;
vType end;
int weight;
}edge;
int Locate(ALGraph &G,vType s)
{//locate the start vertex of one edge in head vertex of the graph
for(int i=0;iadjVertex=e.end;
arc->weight = e.weight;
int headV_i=Locate(G,e.start);
arc->nextEdge=G.HeadVertex[headV_i].firstEdge;
G.HeadVertex[headV_i].firstEdge = arc;
}
void Graph_Create(ALGraph &G, vType V[], edge E[])
{
//init the head vertex
G.HeadVertex= new gVertex[G.vNum];
for( int i=0;i "<< p->adjVertex;
p = p->nextEdge;
}
cout<"<adjVertex<<":";
switch(p->type)
{
case TREE:
cout<<"Tree edge"<nextEdge;
}
}
}
*/
/*--------------------DFS Alogithms-----------------------*/
int time0;
int r_i=0;
void Graph_DFSVisit(ALGraph &G, gVertex *u, vType *r)
{
time0 = time0 +1; //white vertex u has just been discovered
u->d = time0 ;
u->color = GRAY;
gEdge *p = u->firstEdge;
while(p)
{
vType v = p->adjVertex;
int h_i=Locate(G,v);
gVertex *hv = &G.HeadVertex[h_i];
//classify the edge and recursive searching
if( hv->color == WHITE)
{
hv->parent = u->key;
Graph_DFSVisit(G,hv,r);
p->type = TREE; //Tree edge
}
else if(hv->color == GRAY){
p->type = BACK; //Back edge
}
else if(hv->color == BLACK)
{
if(u->d < hv->d)
p->type = FORWARD; //Forward edge
else
p->type = CROSS; //Cross edge
}
p = p->nextEdge;
}
u->color = BLACK; //backen u;it is finished
r[r_i++]=u->key; //store the dfs result into array r
time0 = time0 +1;
u->f = time0;
}
void ALGraph_DFS(ALGraph &G, vType *result)
{
//init all the vertex
gVertex *u;
for(int i=0; icolor = WHITE;
u->parent = '0';
}
time0 = 0; //time stamp
//explore every vertex
for(int i=0; icolor == WHITE)
Graph_DFSVisit(G,u,result);
}
}
/*------------------------------------------------------*/
/*-----------------Topological Sort--------------------*/
bool compare(const gVertex &a,const gVertex &b)
{
return a.f > b.f; //descending order
}
void ALGraph_TSort(ALGraph &G)
{
vType *r = new vType[G.vNum];
ALGraph_DFS(G,r);
//sorting the finished time in descending order
sort(G.HeadVertex,G.HeadVertex+G.vNum,compare); //call the system's sorting function:
}
/*-------------------------------------------------------*/
/*---------------DAG Shortest-Path-----------------------*/
void ShortestPath_Print(ALGraph &G)
{
for(int i=0; id or u->d + w >= INF,it will overflow
if(u->d == INT_MAX || u->d + w >= INT_MAX)
return ;
if(v->d > u->d + w){
v->d = u->d + w;
v->parent = u->key;
}
}
void DAG_ShortestPath(ALGraph &G,vType s)
{
ALGraph_TSort(G);
Init_SingleSource(G,s);
for(int i=0; iadjVertex;
int v_i = Locate(G,t);
gVertex *uNode = &G.HeadVertex[i];
gVertex *vNode = &G.HeadVertex[v_i];
Graph_edgeRelax(uNode,vNode,e->weight);
e = e->nextEdge;
}
}
}
int main(){
vType V[]={'s','t','y','x','z','r'};
edge E[]={{'s','x',6},{'s','t',2},{'t','x',7},
{'t','y',4},{'t','z',2},{'x','y',-1},
{'x','z',1},{'y','z',-2},{'r','s',5},
{'r','t',3}
};
ALGraph G;
G.vNum = sizeof(V)/sizeof(vType);
G.eNum = sizeof(E)/sizeof(edge);
G.kind = DG;
Graph_Create(G,V,E);
cout<<"Please input the starting node:";
vType s;
cin>>s;
DAG_ShortestPath(G,s);
cout<<"The shortest-paths tree is:"<
运行结果:

Dijstra算法完整代码:
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define UDG 0
#define DG 1
#define WHITE 0
#define GRAY 1
#define BLACK 2
#define NONE 0
#define TREE 1
#define BACK 2
#define FORWARD 3
#define CROSS 4
typedef char vType;
typedef struct gEdge{
vType adjVertex; //the adjacency vertex pointed by this edge.
int weight; //the weight of this edge
int type; //the type of edge
gEdge *nextEdge; //Point to the next edge
}gEdge;
typedef struct gVertex{
vType key; // the key of the vertex
int color;
int d,f; // the discovered time and the finished time
vType parent; // the parent node's key after searching
gEdge *firstEdge; // point to the first edge attached to the vertex;
}gVertex;
typedef struct ALGraph{
int vNum;
int eNum;
int kind; //the kind of Graph
gVertex *HeadVertex;
}ALGraph;
typedef struct edge{
vType start;
vType end;
int weight;
}edge;
int Locate(ALGraph &G,vType s)
{//locate the start vertex of one edge in head vertex of the graph
for(int i=0;iadjVertex=e.end;
arc->weight = e.weight;
int headV_i=Locate(G,e.start);
arc->nextEdge=G.HeadVertex[headV_i].firstEdge;
G.HeadVertex[headV_i].firstEdge = arc;
}
void Graph_Create(ALGraph &G, vType V[], edge E[])
{
//init the head vertex
G.HeadVertex= new gVertex[G.vNum];
for( int i=0;i "<< p->adjVertex;
p = p->nextEdge;
}
cout<d = time0 ;
u->color = GRAY;
gEdge *p = u->firstEdge;
while(p)
{
vType v = p->adjVertex;
int h_i=Locate(G,v);
gVertex *hv = &G.HeadVertex[h_i];
//classify the edge and recursive searching
if( hv->color == WHITE)
{
hv->parent = u->key;
Graph_DFSVisit(G,hv,r);
p->type = TREE; //Tree edge
}
else if(hv->color == GRAY){
p->type = BACK; //Back edge
}
else if(hv->color == BLACK)
{
if(u->d < hv->d)
p->type = FORWARD; //Forward edge
else
p->type = CROSS; //Cross edge
}
p = p->nextEdge;
}
u->color = BLACK; //backen u;it is finished
r[r_i++]=u->key; //store the dfs result into array r
time0 = time0 +1;
u->f = time0;
}
void ALGraph_DFS(ALGraph &G, vType *result)
{
//init all the vertex
gVertex *u;
for(int i=0; icolor = WHITE;
u->parent = '0';
}
time0 = 0; //time stamp
//explore every vertex
for(int i=0; icolor == WHITE)
Graph_DFSVisit(G,u,result);
}
}
/*------------------------------------------------------*/
/*-----------------Topological Sort--------------------*/
bool compare(const gVertex &a,const gVertex &b)
{
return a.f > b.f; //descending order
}
void ALGraph_TSort(ALGraph &G)
{
vType *r = new vType[G.vNum];
ALGraph_DFS(G,r);
//sorting the finished time in descending order
sort(G.HeadVertex,G.HeadVertex+G.vNum,compare); //call the system's sorting function:
}
/*-------------------------------------------------------*/
/*---------------Dijkstra Algorithm----------------------*/
struct cmp{
bool operator()(gVertex *a,gVertex *b){
return a->d > b->d;
}
};
void Dijkstra_Print(ALGraph &G)
{
for(int i=0; id or u->d + w >= INF,it will overflow
if(u->d == INT_MAX || u->d + w >= INT_MAX)
return ;
if(v->d > u->d + w){
v->d = u->d + w;
v->parent = u->key;
}
}
/*
void Queue_Print(priority_queue,cmp> q)
{
while(!q.empty())
{
gVertex *t = q.top();
cout<key<<" "<d<,cmp> Q;
//clear queue Q
for(int i=0; i S;//restore the result
while(!Q.empty()){
//Extract minimum of the Queue
gVertex *uNode = Q.top();
Q.pop();
S.push_back(uNode);
int u_i = Locate(G,uNode->key);
gEdge *e = G.HeadVertex[u_i].firstEdge;
while(e)
{
vType v = e->adjVertex;
int v_i = Locate(G,v);
gVertex *vNode = &G.HeadVertex[v_i];
Graph_edgeRelax(uNode,vNode,e->weight);
e = e->nextEdge;
}
//resort priority queue Q
priority_queue,cmp> tQ;
while(!Q.empty()){
tQ.push(Q.top());
Q.pop();
}
Q = tQ;
}
}
int main(){
vType V[]={'s','t','y','x','z'};
edge E[]={{'s','t',10},{'s','y',5},{'t','y',2},{'t','x',1},
{'y','t',3},{'y','x',9},{'y','z',2},{'x','z',4},
{'z','x',6},{'z','s',7}
};
ALGraph G;
G.vNum = sizeof(V)/sizeof(vType);
G.eNum = sizeof(E)/sizeof(edge);
G.kind = DG;
Graph_Create(G,V,E);
cout<<"Please input the starting node:";
vType s;
cin>>s;
Graph_Dijkstra(G,s);
cout<<"The shortest-paths tree is:"<
运行结果:
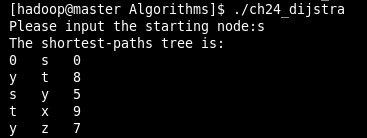
【注:若有错误,请指正~~~】
![]()












