介绍
简单的说，奇异值分解其实就是把一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示，这些小矩阵描述的是矩阵的重要的特性，从而能够让我们从中挑出一些重要的特征来达到降低维度的目的。
SVD其实就是上一节二维降一维的算法的推广，这个算法的主要结果就是我们能够把一个的矩阵写成：
其中：
- 是一个的正交矩阵；
- 是一个的正交矩阵，每一列是一个特征向量；
- 是一个的对角矩阵，对角线上的值就是奇异值，从大到小排列；
- 正交矩阵：若，那么A便是正交矩阵；
- 对角矩阵：主对角线之外的元素皆为0的矩阵。
因为是正交矩阵，所以上边的等式又可以写成：
先来看一下在R中大致是怎么进行奇异值分解并且求出主成分的吧：
library(rafalib)
library(MASS)
n <- 100
#mvrnorm(n,mean,cov)的作用就是随机生成每列100个数值的多元正态分布数据，数据的平均数由mean指定，方差及协方差由协方差矩阵指定。
y <- t(mvrnorm(n,c(0,0),matrix(c(1,0.95,0.95,1),2,2)))
#svd()函数就是奇异值分解的函数,会返回分解出的u、v和d矩阵
s <- svd(y)
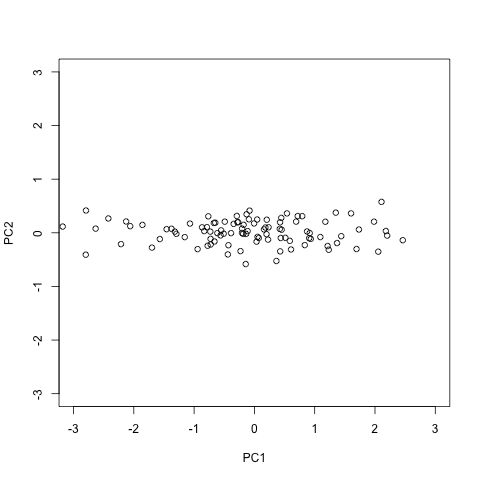
想要从SVD中获得主成分，其实就看的列也就是的列就可：
PC1 <- s$d[1]*s$v[,1]
PC2 <- s$d[2]*s$v[,2]
plot(PC1,PC2,xlim=c(-3,3),ylim=c(-3,3))
1912111534.png
细节
以tissuesGeneExpression包中的基因表达数据为例：
library(tissuesGeneExpression)
data(tissuesGeneExpression)
set.seed(1)
ind <- sample(nrow(e),500)
Y <- t(apply(e[ind,],1,scale))
s <- svd(Y)
U <- s$u
V <- s$v
D <- diag(s$d)
经过计算你就会发现，我们可以拿分解到的这三个矩阵去重构矩阵：
Yhat <- U %*% D %*% t(V)
resid <- Y - Yhat
max(abs(resid))
## [1] 3.508305e-14
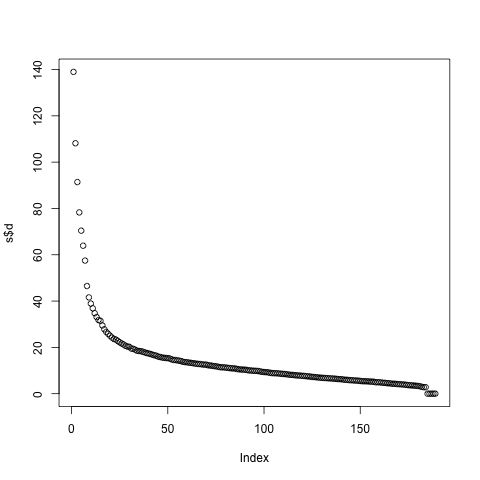
你看，重构的与原始矩阵残差的最大绝对值几乎为0，然后在观察下矩阵的特征值有啥特征：
plot(s$d)
1912111638.png
很明显，越到后面，奇异值越小，也就是矩阵中的特征向量（每一列列）对的重构就越来越不重要，换句话说就是“方差解释度越来越小（explaining less variance）”。比如说我们把最后4个特征向量去掉：
k <- ncol(U)-4
Yhat <- U[,1:k] %*% D[1:k,1:k] %*% t(V[,1:k])
resid <- Y - Yhat
max(abs(resid))
## [1] 3.508305e-14
重构的矩阵与原始矩阵之间的最大残差依旧几乎为0，可见重构效果是很好的。
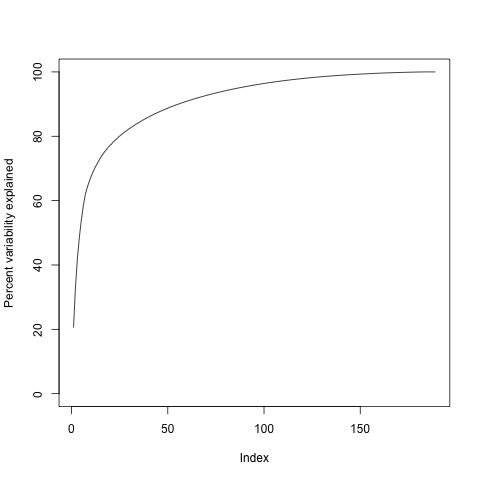
再来看一下方差解释度随着特征向量的变化(累积曲线)：
plot(cumsum(s$d^2)/sum(s$d^2)*100,ylab="Percent variability explained",ylim=c(0,100),type="l")
1912111708.png
从上图中可以看出，index为95时差不多就到达平台期了，所以，我们其实只用前95个特征值就可以重构矩阵：
k <- 95 ##out a possible 189
Yhat <- U[,1:k] %*% D[1:k,1:k] %*% t(V[,1:k])
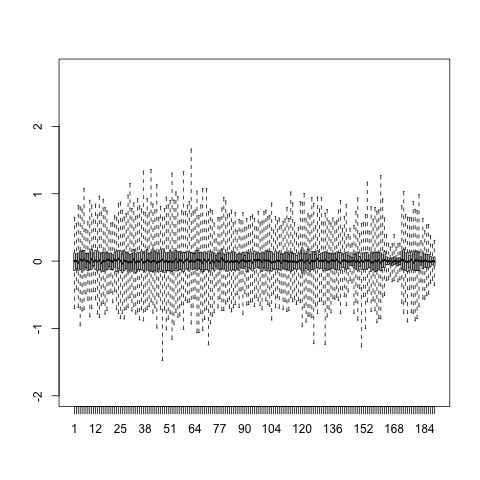
resid <- Y - Yhat boxplot(resid,ylim=quantile(Y,c(0.01,0.99)),range=0)
1912111715.png
可以看到，重构前后的矩阵残差紧密的分布在了的那条直线上了,这时：
var(as.vector(resid))/var(as.vector(Y))
## [1] 0.04076899
也就是说我么解释了96 %的变异，解释度还有另外一种算法：
sum(s$d[1:k]^2/sum(s$d^2))
## [1] 0.04076899
高度相关的数据
实际上，对于高度相关的数据来说，往往第一个奇异值或者说矩阵的第一列几乎就能够解释所有的变异了，我们以另外一个例子说明：
m <- 100
n <- 2
x <- rnorm(m)
e <- rnorm(n*m,0,0.01)
Y <- cbind(x,x)+e
cor(Y)
## x x
## x 1.0000000 0.9998873
## x 0.9998873 1.0000000
d <- svd(Y)$d
d[1]^2/sum(d^2)
## [1] 0.9999441
阅读原文请戳