《算法导论》第23章——最小生成树

  虽然写这个博客主要目的是为了给我自己做一个思路记忆录，但是如果你恰好点了进来，那么先对你说一声欢迎。我并不是什么大触，只是一个菜菜的学生，如果您发现了什么错误或者您对于某些地方有更好的意见，非常欢迎您的斧正！

23.1最小生成树的形成

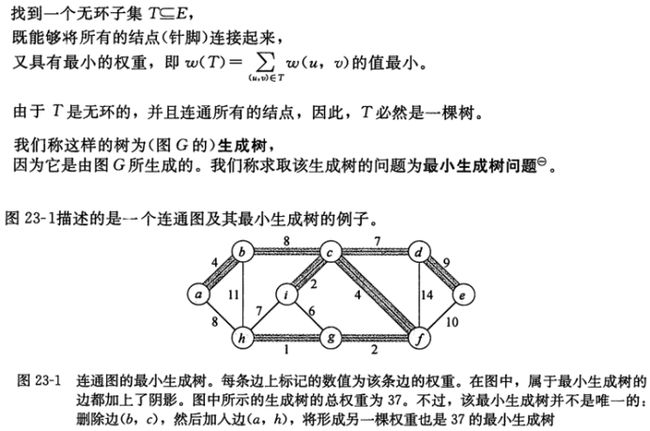
在上图中，就是边cd。

这两个定理看不懂没关系，不影响后面学习Kruskal算法与Prim算法。

23.2Kruskal算法和Prim算法

Kruskal算法
我的理解：
1、寻找权值最小的边，如果边的两个顶点属于不同的集合就加入到A
2、重复过程1，直到找到n-1条边

第一点中分集合的方法我借鉴了wxdjss的博客，以下是他的博客链接
http://www.cnblogs.com/wxdjss/p/5503023.html
方法就是一开始的时候给每棵树都规定一个int，这是它所在的集合，如果找到同伴了，也就是说比如ab边要加入到A中了，那么检索所有的点的int，如果它在集合和a中（也就是这个点的int==a的int），那么就让这颗点的int=b的int，也就是说都加入到b的集合中了。


我写的代码的思路：
1、给每个点分配一个集合，点的属性mark表示在第mark个集合中
2、边从小排到大，依次遍历，如果起点与终点的mark不同（不在同一棵树中），把这条边加入到A中，同时修改起点与终点所在的树的mark，让它们都统一（遍历每个点，所有与起点mark相同的，就赋值为终点的mark）
3、如果A满了，就结束循环

Prim算法



我写的代码的思路：
1、创建一个数组A用来存放已经加入的边
2、每个顶点有一个belong标志着在结合A中（true）还是不在（false）
3、每条边有一个mark标志着是否在集合A中
4、把边从小排到大，遍历每条边，如果不在集合中，如果起点与终点的belong属性不同（表示这条边跨集合），那就把这条边加入到集合A中
5、如果集合A满了（已经有8条边了），结束循环

以下就是代码部分了（建议粘贴到自己的编辑器中运行，虽然我觉得这可能是你点进来唯一会看的部分，为了便于理解，我在上面的文章里都写了这个代码思路。还是谢谢你点进来了！）

Kruskal.h

#pragma once
#define KRUV 9/*点的数量*/
#define KRUE 14/*边的数量*/
/*顶点*/
typedef struct
{
	int mark;/*标记是否在同一棵树中*/
	char data;/*数据*/
}Kruv;

/*边*/
typedef struct
{
	Kruv* start;/*起点*/
	Kruv* end;/*终点*/
	int w;/*权重*/
}Krue;
typedef struct
{
	Kruv* V[KRUV];/*点集*/
	Krue* E[KRUE];/*边集*/
}KruG;

bool cmp(Krue* x, Krue* y);
/*Kruskal算法*/
void MST_Kruskal(KruG* &G);
/*打印边*/
void PrintKru();
/*测试函数*/
void TestKru();

Kruskal.cpp

#include "Kruskal.h"
#include
#include
#include/*sort排序函数所需头文件*/
#include
using namespace std;

Krue* A[KRUV];/*最小生成树的边集*/
/*排序*/
bool cmp(Krue* x, Krue* y)
{
	return x->w < y->w;/*按照权值升序*/
}

/*Kruskal算法*/
void MST_Kruskal(KruG* &G)
{
	sort(G->E, G->E + KRUE, cmp);/*按照权重对边集进行排序*/
	int i, j, k;

	for (i = 0; i < KRUV; i++)/*对每个点进行初始化*/
		G->V[i]->mark = i;/*借鉴一个博主的方法*/

	i = 0;
	j = 0;
	while (jE[i]->start->mark;/*开始的点所在的树*/
		int end = G->E[i]->end->mark;/*结束的点所在的树*/
		if (start!=end)/*不在同一棵树*/
		{
			A[j] = G->E[i];/*把这条边加进去*/

			for (k = 0; k < KRUV; k++)
				if (G->V[k]->mark == start)/*如果与起点同一棵树*/
					G->V[k]->mark = end;/*把它们都加入到终点的树里*/
			i++; j++;
		}
		else
			i++;/*扫描下一条边*/
	}
}
/*打印边*/
void PrintKru()
{
	int weight = 0;
	for (int i = 0; i < KRUV - 1; i++)
	{
		cout << A[i]->start->data << "->" << A[i]->end->data <<":"<w<< endl;
		weight += A[i]->w;
	}
	cout << "总权重：" << weight;
	cout << endl;
}
/*测试函数*/
void TestKru()
{
	Kruv* a = new Kruv(); a->data = 'a';
	Kruv* b = new Kruv(); b->data = 'b';
	Kruv* c = new Kruv(); c->data = 'c';
	Kruv* d = new Kruv(); d->data = 'd';
	Kruv* e = new Kruv(); e->data = 'e';
	Kruv* f = new Kruv(); f->data = 'f';
	Kruv* g = new Kruv(); g->data = 'g';
	Kruv* h = new Kruv(); h->data = 'h';
	Kruv* i = new Kruv(); i->data = 'i';

	KruG* G = new KruG();
	G->V[0] = a; G->V[1] = b; G->V[2] = c;
	G->V[3] = d; G->V[4] = e; G->V[5] = f;
	G->V[6] = g; G->V[7] = h; G->V[8] = i;

	for (int i = 0; i < KRUE; i++)
		G->E[i] = new Krue();

	G->E[0]->start = b; G->E[0]->end = c; G->E[0]->w = 8;/*b-c边*/
	G->E[1]->start = c; G->E[1]->end = d; G->E[1]->w = 7;
	G->E[2]->start = d; G->E[2]->end = e; G->E[2]->w = 9;
	G->E[3]->start = e; G->E[3]->end = f; G->E[3]->w = 10;
	G->E[4]->start = f; G->E[4]->end = g; G->E[4]->w = 2;
	G->E[5]->start = g; G->E[5]->end = h; G->E[5]->w = 1;
	G->E[6]->start = h; G->E[6]->end = a; G->E[6]->w = 8;
	G->E[7]->start = a; G->E[7]->end = b; G->E[7]->w = 4;
	G->E[8]->start = b; G->E[8]->end = h; G->E[8]->w = 11;
	G->E[9]->start = d; G->E[9]->end = f; G->E[9]->w = 14;
	G->E[10]->start = c; G->E[10]->end = i; G->E[10]->w = 2;
	G->E[11]->start = i; G->E[11]->end = h; G->E[11]->w = 7;
	G->E[12]->start = i; G->E[12]->end = g; G->E[12]->w = 6;
	G->E[13]->start = c; G->E[13]->end = f; G->E[13]->w = 4;

	MST_Kruskal(G);
	PrintKru();
}

主函数

#include "Kruskal.h"
#include 

int main()
{
	TestKru();
	getchar();
	getchar();
	return 0;
}

运行结果
这边显示了边加入的顺序

Prim.h

#pragma once
#define PRIMV 9/*点的数量*/
#define PRIME 14/*边的数量*/

/*点*/
typedef struct
{
	char data;/*数据*/
	bool belong;/*标志所在集合：false表示在Q，true表示在A*/
}Primv;

/*边*/
typedef struct
{
	Primv* start;/*起点*/
	Primv* end;/*终点*/
	bool mark;/*是否已经被选中*/
	int w;/*权重*/
}Prime;

/*图*/
typedef struct
{
	Primv* v[PRIMV];/*点集*/
	Prime* e[PRIME];/*边集*/
}Primg;

/*排序函数*/
bool PrimCmp(Prime* x, Prime* y);
/*Prim算法*/
void MST_Prim(Primg* &G, Primv* root);
/*打印边*/
void Prim_Print();
/*测试函数*/
void TestPrim();

Prim.cpp

#include "Prim.h"
#include
#include
#include/*sort排序函数所需头文件*/
#include
using namespace std;

Prime* primA[PRIMV-1];/*最小生成树的边集*/

/*排序函数*/
bool PrimCmp(Prime* x, Prime* y)
{
	return x->w < y->w;/*从小到大排序*/
}

/*Prim算法*/
void MST_Prim(Primg* &G,Primv* root)
{
	int i, j;

	for (i = 0; i < PRIMV; i++)/*对每个顶点进行初始化*/
	{
		G->v[i]->belong = false;/*都在点集Q中*/
	}
	root->belong = true;/*把根放到A里面*/

	for (i = 0; i < PRIME; i++)/*对每条边进行初始化,Q集合是图中的集合减去A，这里没有明示*/
	{
		G->e[i]->mark = false;/*都没有被选中*/
	}

	sort(G->e, G->e + PRIME, PrimCmp);/*按权重对边进行从小到大的排序*/
	j = 0;

	while (j < PRIMV - 1)/*当集合A没有满*/
	{
		for (i = 0; i < PRIME; i++)/*遍历每一条边*/
		{
			if (!G->e[i]->mark)/*这条边还没有加入到A中*/
			{
				if (G->e[i]->start->belong == !(G->e[i]->end->belong))/*如果这条边跨集合*/
				{
					primA[j] = G->e[i];/*把这条边加入到集合A里*/
					G->e[i]->start->belong = true;
					G->e[i]->end->belong = true;
					G->e[i]->mark = true;/*标志这条边已经加入了*/
					j++;
					i = 20;/*结束这个循环*/
				}
			}
		}
	}
}
/*打印边*/
void Prim_Print()
{
	int weight = 0;
	for (int i = 0; i < PRIMV - 1; i++)
	{
		cout << primA[i]->start->data << "->" << primA[i]->end->data << ":" << primA[i]->w << endl;
		weight += primA[i]->w;
	}
	cout << "总权重：" << weight;
	cout << endl;
}
/*测试函数*/
void TestPrim()
{
	/*点集*/
	Primv* a = new Primv(); a->data = 'a';
	Primv* b = new Primv(); b->data = 'b';
	Primv* c = new Primv(); c->data = 'c';
	Primv* d = new Primv(); d->data = 'd';
	Primv* e = new Primv(); e->data = 'e';
	Primv* f = new Primv(); f->data = 'f';
	Primv* g = new Primv(); g->data = 'g';
	Primv* h = new Primv(); h->data = 'h';
	Primv* i = new Primv(); i->data = 'i';

	Primg* G = new Primg();
	G->v[0] = a; G->v[1] = b; G->v[2] = c;
	G->v[3] = d; G->v[4] = e; G->v[5] = f;
	G->v[6] = g; G->v[7] = h; G->v[8] = i;

	for (int i = 0; i < PRIME; i++)
		G->e[i] = new Prime();

	G->e[0]->start = b; G->e[0]->end = c; G->e[0]->w = 8;/*b-c边*/
	G->e[1]->start = c; G->e[1]->end = d; G->e[1]->w = 7;
	G->e[2]->start = d; G->e[2]->end = e; G->e[2]->w = 9;
	G->e[3]->start = e; G->e[3]->end = f; G->e[3]->w = 10;
	G->e[4]->start = f; G->e[4]->end = g; G->e[4]->w = 2;
	G->e[5]->start = g; G->e[5]->end = h; G->e[5]->w = 1;
	G->e[6]->start = h; G->e[6]->end = a; G->e[6]->w = 8;
	G->e[7]->start = a; G->e[7]->end = b; G->e[7]->w = 4;
	G->e[8]->start = b; G->e[8]->end = h; G->e[8]->w = 11;
	G->e[9]->start = d; G->e[9]->end = f; G->e[9]->w = 14;
	G->e[10]->start = c; G->e[10]->end = i; G->e[10]->w = 2;
	G->e[11]->start = i; G->e[11]->end = h; G->e[11]->w = 7;
	G->e[12]->start = i; G->e[12]->end = g; G->e[12]->w = 6;
	G->e[13]->start = c; G->e[13]->end = f; G->e[13]->w = 4;

	Primv* root = a;

	MST_Prim(G, root);
	Prim_Print();
}

主函数

#include "Prim.h"
#include 

int main()
{
	TestPrim();
	getchar();
	getchar();
	return 0;
}

运行结果
这边显示了边加入的顺序：

参考文章及博客：
wxdjss的博客
http://www.cnblogs.com/wxdjss/p/5503023.html