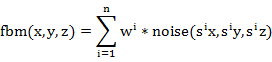柏林噪声进阶-advanced perlin noise
柏林噪声进阶
翻译:则卷大明
原文链接:http://iquilezles.org/www/articles/morenoise/morenoise.htm
原作者 i.q.
译者注:阅读此文需要了解柏林噪声和分型布朗运动相应知识。
一、简介
在这里我会写一些关于柏林噪声的有趣的事实。是的,非常难以置信,你可以在这里找到其他地方没有的信息,少有人谈起的关于柏林噪声的导数,像怎么解析式地对他们进行求解和怎样使用它们。所以,为什么不去做呢?让我们来看看。
噪声导数可以通过非常简单的方法来达到稍微修改传统的fbm形状(fbm:分型布朗运动)的目的。注意,为了获取更好的多样性,依赖于一个规律性的fbm。
解析式的噪声导数的计算比中心差分法更快更准确。基于分形求和函数(fractal sum function)(例如脊背噪声,湍流图等),解析式的法线可以用于完整的高度图的计算。
这张图是通过直接步进(raymarching)过程式函数渲染的(没有法线图,没有材质),仅仅使用了漫反射光照和雾。(译者注:相应的过程式函数也即fbm,可以到shadertoy中搜索i.q.的作品查看)
二、导数
我们用n(x,y,z)来表示3d柏林噪声。当然,它在任何数量的维度上都是相同的。我们采取常用的符号来表示导数:
(3d)噪声函数基于一个给定晶格的随机值的(3线性)线性插值。例如:
![]()
通常u(x)、v(y)、w(z)是一个立方或者五次方多项式的形式:
![]() 或者
或者![]()
n(x, y, z)可以展开成如下公式:
![]()
其中
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
现在导数可以被很简单地计算出来,例如,对于x轴:
其中
![]() 或者
或者![]() ,它依赖于你选择了三次方还是五次方函数。
,它依赖于你选择了三次方还是五次方函数。
因此,它非常简单地构造了一个函数,然后返回这个噪声值,以及在一个函数中计算三个导数,这使得它相比较于中心差分法而言非常的高效,中心差分法慢了5倍。
void dnoise3f( float *vout, const float x, const float y, const float z )
{
int i, j, k;
float u, v, w;
iGetIntegerAndFractional( x, &i, &u );
iGetIntegerAndFractional( y, &j, &v );
iGetIntegerAndFractional( z, &k, &w );
const float du = 30.0f*u*u*(u*(u-2.0f)+1.0f);
const float dv = 30.0f*v*v*(v*(v-2.0f)+1.0f);
const float dw = 30.0f*w*w*(w*(w-2.0f)+1.0f);
u = u*u*u*(u*(u*6.0f-15.0f)+10.0f);
v = v*v*v*(v*(v*6.0f-15.0f)+10.0f);
w = w*w*w*(w*(w*6.0f-15.0f)+10.0f);
const float a = myRandomMagic( i+0, j+0, k+0 );
const float b = myRandomMagic( i+1, j+0, k+0 );
const float c = myRandomMagic( i+0, j+1, k+0 );
const float d = myRandomMagic( i+1, j+1, k+0 );
const float e = myRandomMagic( i+0, j+0, k+1 );
const float f = myRandomMagic( i+1, j+0, k+1 );
const float g = myRandomMagic( i+0, j+1, k+1 );
const float h = myRandomMagic( i+1, j+1, k+1 );
const float k0 = a;
const float k1 = b - a;
const float k2 = c - a;
const float k3 = e - a;
const float k4 = a - b - c + d;
const float k5 = a - c - e + g;
const float k6 = a - b - e + f;
const float k7 = - a + b + c - d + e - f - g + h;
vout[0] = k0 + k1*u + k2*v + k3*w + k4*u*v + k5*v*w + k6*w*u + k7*u*v*w;
vout[1] = du * (k1 + k4*v + k6*w + k7*v*w);
vout[2] = dv * (k2 + k5*w + k4*u + k7*w*u);
vout[3] = dw * (k3 + k6*u + k5*v + k7*u*v);
}
三、改进的fbm(分形布朗运动)
fbm(分形布朗运动)通常通过柏林噪声函数的分形求和来实现。
通常w=1/2以及s=2或者其他接近的值。
(当s=2每个迭代称作一个"octave倍频程"-两倍的频率,就像音乐)。全部的导数是在这种情况下每个倍频程的导数的加权和。如果你用柏林噪声实现了一个脊背图或者其他的变种,你可以以正确的方式轻松地联合这些导数,除非你使用了一个不连续形状的函数,例如fabsf()。(译者注:如果此处不是很理解,可以参考维基百科中FBM的定义)
现在,在这个方案中的一个简单的修改足以给地形增添许多丰富多变的形状,有平坦地区和许多粗糙的区域。
图左(使用u(x)三次方函数渲染,注意不连续的人工痕迹)
图右(使用五次方渲染)
这个地形的计算使用下列分形求和(fractal sum)的变种:
float f = 0.0f;
float w = 0.5f;
float dx = 0.0f;
float dz = 0.0f;
for( int i=0; i < ioct ; i++ )
{
float n[3];
dnoise2f( n, x, y );[1]
dx += n[1];
dz += n[2];
f += w * n[0] / (1.0f + dx*dx + dz*dz); // replace with "w * n[0]" for a classic fbm()
w *= 0.5f;
x *= 2.0f;
y *= 2.0f;
}
左图使用u(x)的三次方版本来计算,另外一个使用五次方。注意左图中有一些不连续的人工痕迹,由于u(x)函数的二阶导数是不连续的。
其他导数的使用也可以产生有趣的形状:
注1:详见i.q.在ShaderToy-Elevated中的实现。下面是其摘抄:
// value noise, and its analytical derivatives
vec3 noised( in vec2 x )
{
vec2 p = floor(x);
vec2 f = fract(x);
vec2 u = f*f*(3.0-2.0*f);
float a = texture2D(iChannel0,(p+vec2(0.5,0.5))/256.0,-100.0).x;
float b = texture2D(iChannel0,(p+vec2(1.5,0.5))/256.0,-100.0).x;
float c = texture2D(iChannel0,(p+vec2(0.5,1.5))/256.0,-100.0).x;
float d = texture2D(iChannel0,(p+vec2(1.5,1.5))/256.0,-100.0).x;
return vec3(a+(b-a)*u.x+(c-a)*u.y+(a-b-c+d)*u.x*u.y,
6.0*f*(1.0-f)*(vec2(b-a,c-a)+(a-b-c+d)*u.yx));
}
其中iChannel0是一张256*256的噪点图。返回的vec3类型中,x表示perlin-noise的值,yz值的计算则是perlin-noise的导数的一个应用。
【版权声明】
原文作者未做权利声明,视为共享知识产权进入公共领域,自动获得授权。