写在前面
线性数据结构指的是元素之间的顺序是由插入和删除所决定的,一个元素被添加,那么它相对于前后项的位置就不变了。在线性数据结构这部分,我们主要了解四种类型,栈,队列,deque,列表,均用python实现,教材Problem Solving with Algorithms and Data Structures using Python http://interactivepython.org/courselib/static/pythonds/index.html
1、什么是栈
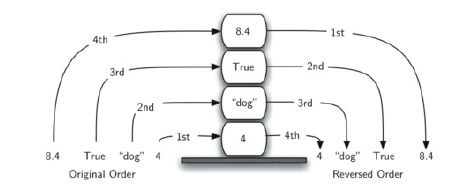
栈是项的有序集合, 它的特点是后进先出(LIFO),添加和移除总发生在一端,我们称之为'顶部',相对应的另一端称之为'底部'。
这种反转的属性可以用到很多地方。 比如当你在浏览网页时,你浏览的网址会被存入栈中,最先浏览的网址在底部,现在浏览的网址在顶部。当你点击网页上的返回键的时候,这些网页按相反的顺序被返回回来。
2、栈的抽象数据类型
在栈中我们定义了以下操作:
stack(): 创建了一个新的空栈
isEmpty(): 判断栈是否为空,为空返回“True”, 不为空返回“False”
push(item): 将item添加到栈顶,它没有返回项,参数为item
pop(): 删除栈顶项,返回item,没有参数
peek(): 返回栈顶项,但并不删除,没有参数
size(): 返回栈中item的数量,不需要参数,返回一个整数
我们使用了列表作为底层实现,列表中的pop()、append()可以实现添加和删除操作。
class stack:
def __init__(self):
self.items=[]
def isEmpty(self): ## 简洁一点的写法return self.items ==[]
if len(self.items)==0:
return True
else:
return False
def push(self,item): #将一个新的项添加到栈的顶部,它需要item做参数并不返回任何内容
self.items.append(item)
def pop(self): #删除栈顶项,返回item,不需要参数
item = self.items.pop()
return item
def peek(self):#返回栈顶的item,但并不会删除它,不需要参数
item = self.items[len(self.items)-1]
return item
def size(self):
return len(self.items)
3、适用问题
在这部分,我们用几个例子说明栈的应用场景。
(1)括号匹配
在使用括号的时候,左括号和右括号成对出现,我们要做的就是对于一连串的括号,判断它们是否匹配。
为什么括号匹配适合用栈处理呢?
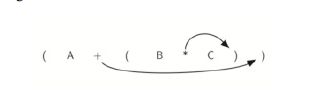
在输入的时候,我们先输入左括号,当出现第一个右括号时,最后出现的左括号与之匹配,而与最后一个右括号相匹配的是最早出现的左括号。右括号以相反的顺序匹配左括号,这是一个可以用栈解决的问题。
算法流程
假设输入为一个只包含括号的字符串,遇到左括号,添加到栈,遇到右括号,则删除栈顶的左括号,这样操作之后,如果括号时匹配的,当右括号使用完,那么栈应该为空。若右括号有剩余,栈为空 或者 栈不为空,右括号无剩余,那么则不匹配。
def parChecker(symbolString):
s = stack()
for item in symbolString:
if item =="(":
s.push(item)
elif item == ")":
if not s.isEmpty():
s.pop()
else: return False # 如果栈为空,但是还有右括号剩余,证明不匹配
if not s.isEmpty():
return False # 如果右括号都没有剩余,但是栈中还有左括号,证明不匹配
return True
延伸 :符号匹配
如果我们匹配的不仅仅是括号,还有 [ ],{ },这就是我们接下来要说的符号匹配了,两者的思想都差不多。唯一一点区别在于,我们遇到的不仅仅是“)”,还有"]", "}",遇到这些符号,我们要删除栈中相应的"(" "]" "}"
def parChecker(symbolString):
s = stack()
symbollist =[ "(","[","{"]
symboldict ={")":0,"]":1,"}":2}
for item in symbolString:
if item in symbollist:
s.push(item)
else:
if s.isEmpty():
return False# 如果栈为空,但是还有右括号剩余,证明不匹配
else:
if symboldict[item] == symbollist.index(s.peek()): # 使用索引值和字典值匹配
s.pop()
else: return False # 字符与栈中字符不匹配
if not s.isEmpty():
return False # 如果右括号都没有剩余,但是栈中还有左括号,证明不匹配
return True
( 2 ) 十进制转化为二进制
为什么进制转换适合用栈处理呢?
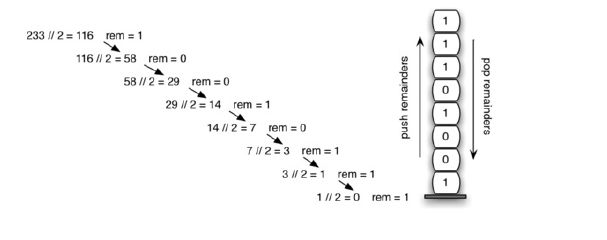
进制转换过程中,我们不断除以进制数,得到余数,最后将余数倒序,就得到了转换后的数。这里再一次出现了反转属性,表明栈可能是解决这个问题的数据结构。
算法流程
假设我们要处理的数字为num, num不断除以2得到余数,添加到栈中,最后将栈中的余数弹出,得到结果。
def divideby2 (num):
s=stack()
binstring=""
while num:
res=num%2
s.push(res)
num = num//2
while not s.isEmpty():
binstring+=str(s.pop())
return binstring
延伸: 任意进制
def dividebybase(num,base):
s=stack()
binstring=""
digits="0123456789ABCDEF"
while num:
res=num%base
s.push(res)
num = num//base
while not s.isEmpty():
binstring+=str(digits[s.pop()])
return binstring
(3) 中缀表达式转后缀表达式
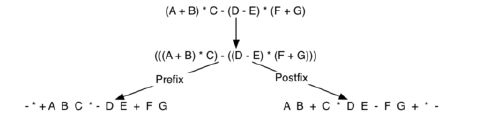
我们平时所写的表达式称为中缀表达式,表示运算符号在两个操作数的中间。同时我们也可以将其写为后缀表达式和前缀表达式,前缀表达式 将所有的运算符都放置在操作数之前,后缀表达式将所有的运算符放在操作数之后。
为什么中缀表达式转为后缀表达式适合用栈处理?
在书中的解释为,因为运算符号存在优先级,所以转换成后缀表达式会出现反转,考虑可以使用栈来处理这样的情况。若只考虑一般的情况,后缀表达式的运算符号顺序是与中缀表达式相反的,从某种程度上说可以用栈来处理。
算法流程
1、新建一个栈s用来保存运算符号和括号,新建一个空列表postfixlist用来保存转换后的中缀表达式
2、将要转换的中缀字符串用字符串拆分方法转换为标记列表
3、遍历标记列表中的每个元素:
若为操作数,则直接添加到postfixlist
若为"("左括号,则直接添加到栈s中
若为操作符,添加到栈s,但要先比较操作符与栈中操作符的优先级,弹出栈中具有更高优先级的操作符到postfixlist,再添加到栈s
若为")",则弹出栈中的操作符直至删除左括号
4、当输入表达式被完全处理时,检查栈中是否还有操作符,若有的话则全部弹出添加到postfixlist
def infixtopostfix(infixexpr):
infixlist = infixexpr.split()
s = stack()
prec={"*":2,"/":2,"+":1,"-":1,"(":0}
postfixlist=[]
for item in infixlist:
if item =="(":
s.push(item)
elif item == ")":
flag=True
while not s.isEmpty() and flag:
if s.peek()!="(":
postfixlist.append(s.pop())
else:
flag = False
s.pop() #当时写程序的时候忘记弹出左括号了
elif item in ["+", "-" ,"*","/"]:
sign = True
while not s.isEmpty() and sign:
if prec[s.peek()]>prec[item]:
postfixlist.append(s.pop())
else: sign = False
s.push(item)
else:
postfixlist.append(item) #若是操作符则加入到列表中
while not s.isEmpty():
postfixlist.append(s.pop())
return " ".join(postfixlist)
str.join(sequence) 指的是用字符str 链接序列sequence中的元素新生成的字符串,sequence是一个对象,如果有多个元素,那么就是元组或者列表,字符串也是可以的。
延伸:后缀表达式求值
因为运算符需要两个操作数,它只与最近的两个操作数有关,而与之前进入的数无关,有点反转的感觉,用栈处理时合适的。
给出一个后缀表达式如何求值呢? 我们可以将操作数添加到栈中,待遇到了操作符,就从栈中弹出两个操作数,在进行运算,运算后的结果再添加到栈中,以便后续运算。最后栈中剩余的数字,就是所求的结果。
def postfixeval(postfixexpr):
postfixlist = postfixexpr.split()
s = stack()
for item in postfixlist:
if item in ["+","-","*","/"]:
op2=s.pop()
op1=s.pop()
res=calculation(op1,op2,item)
s.push(res)
else:
s.push(int(item))
return s.pop()
def calculation(op1,op2,item):
if item=="+":
return op1+op2
elif item=="-":
return op1-op2
elif item=="*":
return op1*op2
else: return op1/op2