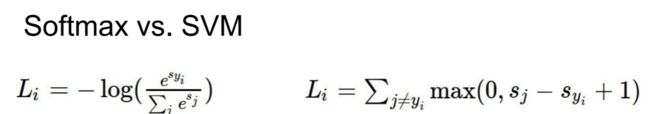关键词:Loss Function、正规化Regularization、 SVM Loss,Softmax Loss (交叉熵损失)
Loss Function
The approach will have two major components:
Score function that maps the raw data to class scores
Loss function tells how good our current classifier is 评价当前的分类器是否理想
We will then cast this as an optimization problem in which we will minimize the loss function with respect to the parameters of the score function.
Multi-class Support Vector Machine loss
SVM支持向量机,知乎上有详解,有兴趣可以去看下。这里只是以SVM的Loss Function为例
s 是 score 的首字母,对应Score Function,模型给某一个样本的分数,事实上s不是一个数字,而是一组数字,因为每个类别都有一个分数。而 sj 就代表对第 j 个类别的分数,这个分数越高就代表样本 xi 越可能属于这个类别。yi 则代表了正确的类别编号。
Hinge Loss
图片中的Loss Function称为 “Hinge Loss”,对于样本 xi --> 得分 s,如果正确类别的得分 s_yi 比错误类别 s_j 的得分高出一定的安全距离(这里就是公式中的1),那么就认为在这个得分的小分量中,损失函数为0,而如果没有达到这个条件,还差多少损失就是多少。
安全距离是否一定要是1?
这个安全距离其实是无所谓的,可以定义为任意数值。因为我们事实上只关心样本有没有被正确的分类,而这些得分的绝对大小其实并没有太大意义,我们更关心的是他们之间的相对大小。也就是说,如果把权重W的数值整体放大为原来的两倍,那么得分s也会随之变为原来的两倍,但他们之间的相对大小关系是没有改变的,这个时候就相当于把安全距离从1变成了2。因此,不同的安全距离事实上只能产生一个放缩的作用,最后得出的分类器在本质上是一样的.
拓展 Squared hinge loss
You’ll sometimes hear about people instead using the squared hinge loss SVM (or L2-SVM), which uses the form max(0,−)^2 that penalizes violated margins more strongly (quadratically instead of linearly). The unsquared version is more standard, but in some data sets the squared hinge loss can work better. This can be determined during cross-validation.
Q2: what is the min/max possible loss?
hinge loss的取值范围:(0,正无穷大),当识别正确的类别的得分 >(错误类别的得分+1)时,取最小值0。
Q3: At initialization W is small so all s ≈ 0. What is the loss?
假设有n个类别,那么对于上述loss function,将会有n-1个求max的算式求和。当s ≈ 0,这n-1个算式的结果都为 1,所以Loss = n -1 .
在实际计算的时候,最开始我们会给权重w初始化为一组随机数字,在这个时候得出的所有分数大小都是相近的, 这种情况下根据损失函数的定义,损失函数应该接近 C - 1(C是类别的数量)。这是一个很好的debug技巧,如果最开始的损失函数数值与之相差太远的话,很可能存在bug。
Q: Suppose that we found a W such that L = 0. Is this W unique?
No! 2W is also has L = 0! 如果把权重W的数值整体放大为原来的两倍,那么得分s也会随之变为原来的两倍,但他们之间的相对大小关系是没有改变的。
对于Loss Function 正规化
所以我们对Loss Function进行正规化
正则化损失:用来衡量模型的复杂程度的,强迫模型趋于更加简单,避免过拟合
解决什么问题?
针对 L = 0 ,希望得到一个独特的W(避免出现W,2W这种情况)。我们希望能像某些特定权重W添加一些偏好,对其他权重则不添加,以此来消除模糊性。如加上L2范式,对于W和2W,2W的惩罚会高于W,所以最终的结果会是W。
λ 是一个超参数,用来确定数据损失和正则化损失之间的相对权重。如果λ比较大,则说明我们更看重正则化损失,如果比较小,就说明更看重数据损失。λ 过大了会造成欠拟合问题,过小会造成过拟合问题。
R(W)就是关于正则化损失具体的定义了,常用的有L1正则化和L2正则化(推荐)等,见下图
L1 权重矩阵 w 所有分量的绝对值之和,L2 权重矩阵 w 所有分量的平方和 (似乎和曼哈顿距离和欧式距离相似)
L1正则化对于所有的损失是线性的,也就是说,10个数据点,每个点误差1个单位,和是完全等价的。
L2正则化由于平方的原因,对那些偏差特别大的点具有很大的惩罚。(1个数据点,误差10单位)的惩罚远远大于 (10个数据点,每个点误差1个单位)。
正是由于这个原因,L2正则化倾向于把权重均匀分布在每一个分量上,而L1正则化则倾向于将更多的权重清零,只保留几个大权重,他们对于模型的“复杂度”的定义是不一样的。示例如下:
对于w1,如果是 L1 正则化 ,R(w1) = 1,如果是 L2 正则化 ,R(w1) = 1
对于w2, 如果是 L1 正则化 R(w1) = 1,如果是 L2 正则化 ,R(w2) = 0.25
为了让Loss Function最小,当 L1 正则化,w1 , w2 都可行;如果是 L2 正则化,那么 w2 更优。
Softmax classifier
如果大家对逻辑回归有基础的话,那么softmax分类器可以当成一个多分类的逻辑回归。
Softmax分类器对应的Loss Function称为 交叉熵损失/cross-entropy loss,就是下图最下方的公式
对于上图的解释:
首先把得分s变成一个概率分布,即所有分量都在0到1之间,并且所有分量的和为1。 然后根据得到的概率分布计算损失 Li。
从直观上理解,交叉熵损失是把我们转化而来的概率分布与最理想的概率分布进行对比,衡量了二者之间的差距。最理想的概率分布就是正确的类别概率为1,其他所有类别的概率都是0。
计算过程,示例如下:
1. (假设得分s是未标准化的对数概率)对每个得分数值计算其指数次幂
2. 然后对于得到的所有值再做一个归一化的操作
3. 最后把正确分类的那个概率值带到LOSS计算公式,就完成啦
Q1:What is the min/max possible loss L_i?
最小值为0,当cat的得分趋近于正无穷,概率为1,其他的概率为0时,计算结果为0
最大值为正无穷大,当cat的概率无限接近于0,Li将趋近于正无穷大。
Q2: Usually at initialization W is small so all s ≈ 0. What is the loss?
在实际计算的时候,最开始我们会给权重w初始化为一组随机数字,在这个时候得出的所有分数大小都是相近的, 这种情况下根据损失函数的定义,损失函数应该接近 logC(C是类别的数量),也可以用来做debug。 (0,logC)之间的一个值
SVM vs Softmax
最明显的区别就是LOSS值的计算方式,SVM是计算的分值的一个差值情况,SOFTMAX看的则是分类的准确率。
示例:
case1:对于 [10,-2,3] SVM Loss = 0,Softmax Loss = 0.000399
改为[9,-2,3] SVM Loss = 0,Softmax Loss = 0.001082 (略有增大)
case2:对于 [10,9,9] SVM Loss = 0,Softmax Loss = 0.239489
改为[9,9,9] SVM Loss = 2,Softmax Loss = log 3 = 0.477121
SVM - Hinge Loss
只要样本满足边界条件,(正确类别的得分 > 错误类别得分+ 1 margin)之后就不进行优化了,因为此时的损失函数不会再减小了。
Softmax - Cross-Entropy Loss
只要样本发生变化,损失函数就会发生变化(即使变化值很小)。根据定义,想要得到理想的概率分布,势必要让正确类别的得分趋近于正无穷,错误类别的得分趋近于负无穷,所以模型会不断的优化参数,试图去迫近这个最理想的概率分布。(任何一个测试样本都会影响分类器性能)
参考文章:
http://www.mamicode.com/info-detail-2088132.html
http://blog.csdn.net/tangyudi/article/details/52098520?locationNum=14
cs231n 网站上有很棒的英文版笔记,在课程网站上,所有以notes结尾的链接中,比如本章相关的notes