递归->栈->队列面试题

本文所有程序均已测试通过，测试结果图就不一个一个再截图了；读者可以自己copy验证一下；后期我会把思路图补出来

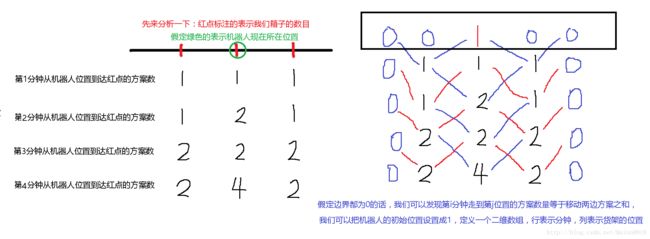
1.行走机器人问题：货架N个，机器人初始位置在pos，经过minutes分钟后到达T有多少种方案

//行走机器人问题：货架N个，机器人初始位置在pos，经过minutes分钟后到达T有多少种方案
int Walkrobb(int n, int pos, int minutes, int t)
{
    while (n >= 0 && pos >= 0 && minutes >= 0 && t >= 0)
    {
        int arr[100][100];
        memset(arr, 0, sizeof(arr));
        arr[0][pos] = 1;
        for (int i = 1; i <= minutes; i++)//第i分钟
        {
            for (int j = 1; j <= n; j++)//第j位置
            {
                arr[i][j] = arr[i-1][j + 1] + arr[i-1][j - 1];
                //第i分钟走到第j位置的方案等于移动两边方案之和
            }
        }
        return arr[minutes][t];
        //返回第minutes分钟走到t位置的方案
    }
    return 0;
}

int main()
{
    int num = Walkrobb(3, 2, 4, 2);
    cout << num << endl;
    system("pause");
}

2.迷宫

回溯法
基本思想：对一个包括有很多个结点，每个结点有若干个搜索分支的问题，把原问题分解为多若干个子问题求解的算法；当搜索到某个结点发现无法再继续搜索下去时，就让搜索过程回溯(回退)到该节点的前一个结点，继续搜索该节点外的其他尚未搜索的分支；如果发现该结点无法再搜索下去，就让搜索过程回溯到这个结点的前一结点继续这样的搜索过程；这样的搜索过程一致进行到搜索到问题的解或者搜索完了全部可搜索分子没有解存在为止。

#define ROW 3
#define COL 6
struct seat
{
public:
    seat(int x,int y)
    :_x(x)
    , _y(y)
    {}
    int _x;
    int _y;
};

class maze
{
public:
    maze(int arr[ROW][COL])
    {
        for(int i = 0; i < ROW; i++)
        {
            for(int j = 0; j < COL; j++)
            {
                _map[i][j] = arr[i][j];
            }
        }
    }

    bool IsPass(const seat &s)
    {
        if (_map[s._x][s._y] == 1)
            return true;
        return false;
    }

    bool PassMaze(const seat &s)
    {
        if (s._x < 0 || s._y >= COL || s._x >= ROW || s._y < 0)
        {
            return true;
        }
        if (IsPass(s))
        {
            _map[s._x][s._y] = 2;

            seat up(s._x - 1, s._y);
            seat down(s._x + 1, s._y);
            seat left(s._x, s._y - 1);
            seat right(s._x, s._y + 1);

            if (PassMaze(up))
            {
                return true;
            }
            else if (PassMaze(left))
            {
                return true;
            }
            else if (PassMaze(right))
            {
                return true;
            }
            else if (PassMaze(down))
            {
                return true;
            }
            else
            {
                _map[s._x][s._y] = 3;
            }

        }
        return false;
    }

    void PrintMap()
    {
        for (int i = 0; i < ROW; i++)
        {
            for (int j = 0; j < COL; j++)
            {
                cout << _map[i][j]<<" ";
            }
            cout << endl;
        }
        cout << endl;
    }
private:
    int _map[ROW][COL];
};

int main()
{
    int arr[ROW][COL] =
    { 
        { 0, 1, 0, 0, 0, 0 }, 
        { 0, 1, 1, 0, 0, 0 }, 
        { 0, 0, 1, 0, 0, 0 }
    };
    maze m(arr);
    m.PrintMap();
    m.PassMaze(seat(2, 2));
    m.PrintMap();
    system("pause");
}

3.括号匹配问题（用栈实现）

解题思路：
（1）只要遇到左括号进压栈；
（2）遇到右括号并且栈不为空，则检测是否与当前栈顶的左括号匹配；如果匹配，则栈顶左括号出栈；如果不匹配，则括号不对应；如果栈空了，则右括号多余；
（3）循环以上步骤
（4）最后如果栈空了，则匹配正确；否则，左括号多余

#include 

class IsBarcketMate
{
public:
    IsBarcketMate(char *arr ="")
        :_arr(arr)
    {
    }

    bool IsBarcket()
    {
        stack<char>h;
        size_t i =0;
        while (i < strlen(_arr) && _arr && *_arr!='\0')
        {
            //出现左括号则进栈
            if (*_arr == '(' || *_arr == '{' || *_arr == '[')
            {
                h.push(*_arr);
                _arr++;
            }
            //出现右括弧
            else if (*_arr == ')' || *_arr == '}' || *_arr == ']')
            {
                //首先检测栈是否为空并且和栈顶数据比较，若匹配则栈顶出栈
                if (!h.empty() && ((h.top() == '(') && (*_arr == ')') || (h.top() == '{') && (*_arr == '}') || (h.top() == '[') && (*_arr == ']')))
                {
                    h.pop();
                    _arr++;
                }
                //若栈空则表明此右括号多余，表达式不匹配
                else if (h.empty())
                {
                    cout <<"右括号多余"<< endl;
                    return false;
                }
                //否则括号不对应
                else
                {
                    cout << "括号不匹配" << endl;
                    return false;
                }
            }
            //处理除了括号以外的字符
            else
            {
                _arr++;
            }
        }
        //最后若栈空，则匹配正确，否则栈里还有左括号
        if (h.empty())
        {
            cout << "括号匹配" << endl;
            return true;
        }
        else
        {
            cout << "左括号多余" << endl;
            return false;

        }
    }
private:
    char *_arr;
};

void test()
{
    char arr1[] = "((()))";
    char arr2[] = "((())))";
    char arr3[] = "(((()))";
    char arr4[] = "(1244ki)";
    char arr5[] = "{([])}";

    IsBarcketMate s1(arr1);
    IsBarcketMate s2(arr2);
    IsBarcketMate s3(arr3);
    IsBarcketMate s4(arr4);
    IsBarcketMate s5(arr5);
    s1.IsBarcket();
    s2.IsBarcket();
    s3.IsBarcket();
    s4.IsBarcket();
    s5.IsBarcket();

}

int main()
{
    test();
    system("pause");
}

4.假设有一个能装入总体积为T的背包和n件体积分别为w1,w2,…wn的物品，能否从n件物品中挑选若干件恰好装满背包，即使w1+w2+…+wm=T，要求找出所有满足上述条件的解。（用栈实现）

解题思路：
（1）首先，将物品排成一列，然后，顺序选取物品装入背包;
（2）若已选取第i件物品后未满，则继续选取第i + 1件;
若该件物品“太大”不能装入，则弃之，继续选取下一件;
若背包满了，则输出，并且丢弃最后进来的物品;
（3）如果在剩余的物品中找不到合适的物品以填满背包，则说明“刚刚”装入的物品“不合适”，应将它取出“弃之一边”，继续再从“它之后”的物品中重新选取；
（4）重复以上步骤，直到没有物品可以放；
（5）换栈底，也就是抛弃最底层的元素，让下一个开始匹配，
（6）重复以上步骤，直到没有物品作栈底；

#include 
class  Backpack
{
public:
    Backpack(int *arr)
    {
        _arr = arr;
    }

    void IsBackpack(int t,int n)
    {
        stack<int>h;
        int count = 0;//计算总和
        int i = 0;//当前压栈的件数
        bool key = false;//判断是否有解
        int border = n;
        //如果没有其他物品可以作为栈底,停止循环
        //外层循环用来挪动栈底
        while (i < n)//循环条件i从0开始，对应的是n的下标
        {

            //判断栈底是否为t;如果是t，则直接输出；跳到下一个元素作为栈底，并且总件数-1；
            if (*_arr == t)
            {
                cout << *_arr << endl;
                --n;
                _arr++;
                key = true;      //到这就说明有解，把key设置成true
            }

            //newarr表示当前栈底；
            int *Newarr = _arr;

            int m = n;
            int j = 0;
            //如果没有其他物品可以选入背包
            //内层循环是在确定了栈底的基础上，挪动其他件数
            while(i < m)
            {

                h.push(Newarr[j]);//把当前元素压进去（第一次循环压进去的栈底）
                i++;            //件数+1
                count += Newarr[j];//count计数

                //如果背包刚好满了
                if (t - count == 0)
                {
                    //则输出当前解
                    stack<int> s(h);
                    while (!s.empty())
                    {
                        cout << s.top() << " ";
                        s.pop();
                    }
                    cout << endl;


                    count -= h.top();//count减去栈顶元素值
                    h.pop();         //释放栈顶元素
                    j++;        //跳到下一个元素
                    key = true;      //到这就说明有解，把key设置成true
                }

                //如果背包没满，则跳到下一个元素；
                else if (t - count > 0)
                {

                    j++;
                }

                //背包溢出，释放栈顶元素；count减去当前值
                else
                {

                    count -= h.top();
                    h.pop();
                    j++;    
                }


//如果在剩余的物品中找不到合适的物品以填满背包，则说明“刚刚”装入的物品“不合适”，
//应将它取出“弃之一边”，继续再从“它之后”的物品中重新选取。

                if (i == m )//当物品放完了，还是没有合适的填满背包（最后一个物品被认为太大，已经在前面释放）
                                             //说明上一个物品不合适,也就是当前的栈顶元素；
                {
                    count -= h.top();//count减去“不合适”物品体积

                    //找到“不合适”物品的坐标
                    for (int k = 0; k < sizeof(Newarr); k++)
                    {
                        if (Newarr[k] == h.top())
                        {
                            j = k;
                            break;
                        }
                    }
                    h.pop();//丢弃它
                    --m;    //总件数减1
                    i = h.size();//设置当前件数为栈元素个数
                    j++;//跳过它，重新取后面的物品

                }
            }


            //释放栈空间，准备换栈底
            while (!h.empty())
            {
                h.pop();
            }
            --n;//总件数减1
            _arr++;//跳到下一个元素
            i = 0;//件数归0
            count = 0;//总和归0
        }


        //无解
        if (!key)
        {
            cout << "无解"<< endl;
        }

    }


private:
    int *_arr;
};


void test()
{
    int arr[6] = {1,8,4,3,5,2};
    Backpack b(arr);
    b.IsBackpack(10,6);

}

int main()
{
    test();
    system("pause");
}

5.两个栈实现一个队列

解题思路：

实现一：

s1是入栈的，s2是出栈的；
入队列，直接压到s1是就行了；
出队列，先把s1中的元素全部出栈压入到s2中，弹出s2中的栈顶元素；再把s2的所有元素全部压回s1中。

实现二：

上述思路，可行性毋庸置疑。但有一个细节是可以优化一下的。即：在出队时，将s1的元素逐个“倒入”s2时，原在s1栈底的元素，不用“倒入”s2（即只“倒”s1.size( )- 1个），可直接弹出作为出队元素返回。这样可以减少一次压栈的操作。

实现三：

入队时，先判断s1是否为空;
如不为空，说明所有元素都在s1，此时将入队元素直接压入s1；
如为空，要将s2的元素逐个“倒回”s1，再压入入队元素。

出队时，先判断s2是否为空；
如不为空，直接弹出s2的栈顶元素并出队；
如为空，将s1的元素逐个“倒入”s2，把最后一个元素弹出并出队。

比较方案一和方案三：
相对于方案一，方案三的s2好像比较“懒”，每次出队后，并不将元素“倒回”s1，如果赶上下次还是出队操作，效率会高一些，但下次如果是入队操作，效率不如第一种方法。入队、出队操作随机分布时，上述两种方法总体上时间复杂度和空间复杂度应该相差无几（无非多个少个判断）。

实现四
s1是入栈的，s2是出栈的。
入队列：直接压入s1即可
出队列：如果s2不为空，把s2中的栈顶元素直接弹出；否则，把s1的所有元素全部弹出压入s2中，再弹出s2的栈顶元素比较
这个思路，避免了反复“倒”栈，仅在需要时才“倒”一次。

//实现方案四
#include 
template <class T>
class MyQueue
{
public:
    void push(T elem) 
    {
        s1.push(elem);
        back_elem = elem;
    }

    void pop() 
    {
        if (!s2.empty()) 
        {
            s2.pop();
        }
        else if (!s1.empty()) 
        {
            while (!s1.empty()) 
            {
                s2.push(s1.top());
                s1.pop();
            }
            s2.pop();
        }
        else 
        {
            cout << "error pop(), empty queue!" << endl;
        }
    }

    T front()
    {
        if (!s2.empty()) 
        {
            return s2.top();
        }
        else if (!s1.empty()) 
        {
            while (!s1.empty()) 
            {
                s2.push(s1.top());
                s1.pop();
            }
            return s2.top();
        }
        else 
        {
            cout << "error front(), empty queue!" << endl;
        }
    }

    T back(){
        if (!empty())
            return back_elem;
        else {
            cout << "error back(), empty queue!" << endl;
            return 0;
        }
    }

    int size() const 
    {
        return s1.size() + s2.size();
    }

    bool empty() const 
    {
        return s1.empty() && s2.empty();
    }
private:
    stack s1;
    stack s2;
    T back_elem;

};

6.两个队列实现一个栈

解题思路：

实现一：

q1是专职进出栈的，q2只是个中转站；
入栈：直接入队列q1即可；
出栈：把q1的除最后一个元素外全部转移到队q2中, 然后把刚才剩下q1中的那个元素出队列。之后把q2中的全部元素转移回q1中。

实现二：

其中一个是专职进出栈的，另一个是中转站，可交替入栈：直接入队列q1即可；

出栈：把q1的除最后一个元素外全部转移到队q2中, 然后把刚才剩下q1中的那个元素出队列。之后不需要把q2中的全部元素转移回q1中
此时，q2作为专职进出栈的，q1作为中转站。避免了重复“倒”数据

//实现方案二
#include 
template <class T>
class Stack
{
public:
    Stack() 
    {
        q1_used = true;
        q2_used = false;
    }

    void push(T elem) 
    {
        if (q1_used == true) 
        {
            q1.push(elem);
        }
        if (q2_used == true)
        {
            q2.push(elem);
        }
    }

    void pop() 
    {
        if (!q1.empty() && q1_used == true) 
        {
            while (q1.size() != 1) 
            {
                q2.push(q1.front());
                q1.pop();
            }
            q1.pop();
            q2_used = true;
            q1_used = false;
            return;
        }
        if (!q2.empty() && q2_used == true) 
        {
            while (q2.size() != 1) 
            {
                q1.push(q2.front());
                q2.pop();
            }
            q2.pop();
            q2_used = false;
            q1_used = true;
            return;
        }
        cout << "error pop()" << endl;
    }


    T top() const {
        if (!q1.empty() && q1_used == true) 
        {
            return q1.back();
        }
        else if (!q2.empty() && q2_used == true) 
        {
            return q2.back();
        }
        cout << "error top()" << endl;
        return 0;
    }

    bool empty() const 
    {
        return q1.empty() && q1_used == true || q2.empty() && q2_used == true;
    }

    int size() const 
    {
        if (!q1.empty() && q1_used == true) 
        {
            return q1.size();
        }
        if (!q2.empty() && q2_used == true) 
        {
            return q2.size();
        }
        return 0;
    }
private:
    queue q1;
    queue q2;
    bool q1_used, q2_used;
};

7.实现一个栈，要求Push（入栈），Pop（出栈），Min（返回最小值的操作）的时间复杂度为O（1）

解题思路：

方法一 ：

使用一个栈；元素x入栈时，执行一次push（x），再push（min），min表示当前栈顶到栈底元素最小值；元素出栈时，执行两次pop（）；

这种方案有缺陷：
如果我们要入栈的元素序列是递增的（1，2，3……1000），那么每一次入栈都要push（1），操作冗余。

方法二：

使用两个栈s1和s2，s2做为辅助栈（每次压入s2的都是s1的最小值）；

元素x入栈时，将x和s2栈顶元素做比较，
如果x小于等于s2.top（），将x分别push到s1和s2，否则x只push到s1；

元素出栈时，将s1栈顶元素和s2栈顶元素做比较，
如果s1.top（）等于s2.top（），s1和s2都执行pop操作，否则只执行
s1.pop（）；

 //实现方案二
#include
typedef int T;
class StackWithMin
{
public:
    StackWithMin()
    {}
    ~StackWithMin()
    {}
    void Push(T x)
    {
        s1.push(x);
        if (s2.empty() || x <= s2.top())
        {
            s2.push(x);
        }
    }
    void Pop()
    {
        if (s1.top() == s2.top())
        {
            s2.pop();
        }
        s1.pop();
    }
    void Min()
    {
        if (!s2.empty())
        {
            cout << s2.top() << endl;
        }

    }
    void Print()
    {
        while (!s1.empty())
        {
            cout << s1.top() << "->";
            s1.pop();
        }
        cout << endl;
        while (!s2.empty())
        {
            cout << s2.top() << "->";
            s2.pop();
        }
        cout << endl;
    }
private:
    stack<int> s1;
    stack<int> s2;
};

void Test()
{
    StackWithMin  s;
    s.Push(4);
    s.Push(3);
    s.Push(5);
    s.Push(2);
    s.Push(1);
    s.Pop();
    s.Min();
    s.Print();

}

int main()
{
    Test();
    system("pause");
}

8.用一个数组实现两个栈（贡献栈）

解题思路：

方案一：偶奇数压栈

将数组的下标为0的位置当做第一个栈的栈底，下标为1的位置当做第二个栈的栈底，将数组的偶数位置看做第一个栈的存储空间，奇数位置看做第二个栈的存储空间。

方案二：从中间分别向两边压栈

将数组的中间位置看做两个栈的栈底，压栈时栈顶指针分别向两边移动，当任何一边到达数组的起始位置或是数组尾部，则开始扩容。

方案三：从两边向中间压栈

将数组的起始位置看作是第一个栈的栈底，将数组的尾部看作第二个栈的栈底，压栈时，栈顶指针分别向中间移动，直到两栈顶指针相遇，则扩容。

方案比较：
（1）扩容条件

方案一和方案二明显在扩容时考虑的情况比较复杂，条件更多一些；方案三在扩容的时候只需要判断两个栈顶相遇了，就扩容。

（2）空间使用率：

方案一和方案二只要其中一个栈压入比较多的数据，而另外一个栈压入的数据很少时，就存在非常大的空间浪费；

就比如说方案一偶奇数压栈：我要是只压偶数栈，不压奇数栈，浪费的空间太多了。。。。

所以比较而言，方案三就可以很好的避免这一情况，空间利用率比较高，
而且这种方案在一个栈pop的空间另一个栈也可以使用，可以在一些情况下减少开辟空间的次数（毕竟在c++中动态开辟空间还是很耗时的）

//实现方案三
template
class TwoStack
{
public:
    TwoStack()
        :_a(NULL)
        , _top1(0)
        , _top2(0)
        , _capacity(0)
    {
        _CheckCapacity();
    }
    ~TwoStack()
    {
        if (_a)
            delete[] _a;
    }
    void Push1(const T& d)
    {
        _CheckCapacity();
        _a[_top1++] = d;
    }
    void Push2(const T& d)
    {
        _CheckCapacity();
        _a[_top2--] = d;
    }
    void Pop1()
    {
        if (_top1 > 0)
            --_top1;
    }
    void Pop2()
    {
        if (_top2 < _capacity - 1)
            _top2++;
    }
    size_t Size1()
    {
        return _top1;
    }
    size_t Size2()
    {
        return _capacity - 1 - _top2;
    }
    bool Empty1()
    {
        return _top1 == 0;
    }
    bool Empty2()
    {
        return _top2 == _capacity - 1;
    }
    T& Top1()
    {
        if (_top1>0)
        {
            return _a[_top1 - 1];
        }
    }
    T& Top2()
    {
        if (_top2 < _capacity - 1)
            return _a[_top2 + 1];
    }

private:
    void _CheckCapacity()
    {
        if (_a == NULL)
        {
            _capacity += 3;
            _a = new T[_capacity];
            _top2 = _capacity - 1;
            return;
        }
        if (_top1 == _top2)
        {
            size_t OldCapacity = _capacity;
            _capacity = _capacity * 2;
            T* tmp = new T[_capacity];
            for (size_t i = 0; i < _top1; i++)
            {
                tmp[i] = _a[i];
            }
            for (size_t j = OldCapacity - 1, i = _capacity - 1; j>_top2; j--, i--)
            {
                tmp[i] = _a[j];
            }
            delete[] _a;
            _a = tmp;
            _top2 += _capacity / 2;
        }
    }

private:
    T* _a;
    size_t _top1;
    size_t _top2;
    size_t _capacity;
};

void Test()
{
    TwoStack<int> s;
    s.Push1(1);
    s.Push1(2);
    s.Push1(3);
    s.Push1(4);
    s.Push1(5);
    s.Push2(1);
    s.Push2(2);
    s.Push2(3);
    s.Push2(4);
    s.Push2(5);
    cout << "s1:" << s.Size1() << endl;;
    cout << "s2:" << s.Size2() << endl;
    while (!s.Empty1())
    {
        cout << s.Top1() << endl;
        s.Pop1();
    }
    while (!s.Empty2())
    {
        cout << s.Top2() << endl;
        s.Pop2();
    }

}

int main()
{
    Test();
    system("pause");
}

9.元素出栈、入栈顺序的合法性

如入栈的序列（1,2,3,4,5），出栈序列为（4,5,3,2,1）

解题思路：

大体是这样的：
定义两个顺序表存放这两个序列；
把第一个序列中的数字依次压入栈中，边压边按照第二个序列的顺序依次从栈中弹出数字。

具体思路：

大前提是：两个序列的元素个数是一样的，否则，不匹配；

入栈顺序表中的元素开始压栈；
遍历出栈顺序表中的元素，有两种情况 ：
（1）如果当前元素是栈顶的元素，则pop出来；
（2）如果不是栈顶元素，则根据入栈顺序将没入栈的元素push进栈，直到将该元素push栈中，然后将该元素pop出来；
（3）重复以上步骤
（4）最后辅助栈为空栈，那么该序列就是合格的；否则，不合格；

#include 
#include 
bool IsPopOrder(vector<int>pushV, vector<int>popV)
{
    if (pushV.size() != popV.size())
        return false;
    int len = pushV.size();
    int indexPopV = 0;
    stack<int> s;
    for (int i = 0; i < len; ++i)
    {
        s.push(pushV[i]);
        while (s.size()!=0 && s.top() == popV[indexPopV])
        {
            s.pop();
            indexPopV++;
        }
    }

    if (s.empty())
    {
        return true;
    }
    return false;
}


void test()
{
    vector<int>pushV = { 1, 2, 3, 4, 5 };       //入栈序列
    vector<int>popV = { 4, 5, 3, 2, 1 };      //出栈序列
    bool ret = IsPopOrder(pushV, popV);
    if (ret)
        cout << "出栈顺序合法" << endl;
    else
        cout << "出栈顺序不合法" << endl;
}

int main()
{

    test();
    system("pause");
}