每天一道leetcode-153
前言
目前准备每天刷一道题leetcode的题目,以此来激励那些零基础入门的人,千万不要被什么科班和非科班的说法吓倒了,计算机这个行业只要你肯努力,没有什么逾越不了的鸿沟。
只要你肯努力,一份努力,一份汗水,在程序员这个职业,你的每一份付出都会得到对应的那一份汇报,尊重学习规律,循序渐进,别想着一口吃个胖子,罗马也不是一天建成的,有朝一日,你终会变成你想成为的人。
题目目前可能需要一定的算法与数据结构基础才能看懂,后序会写一下零基础也能看懂的入门知识,然后就可以看懂我编写的题目了~
案例
题目
leetcode-153 寻找旋转排序数组中的最小值
tag(分类): 二分查找这一类
链接:
https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/
题目详述
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
你可以假设数组中不存在重复元素。
示例 1:
输入: [3,4,5,1,2]输出: 1
示例 2:
输入: [4,5,6,7,0,1,2]输出: 0
题解
代码
1class Solution {
2 public int findMin(int[] nums) {
3 if(nums.length == 1)
4 return nums[0];
5 if(nums[0] < nums[nums.length-1])
6 return nums[0];
7 int left = 0;
8 int right = nums.length - 1;
9 while(left <= right)
10 {
11 int mid = left + (right-left)/2;
12 if(mid+11] && nums[mid] < nums[mid-1])
13 {
14 return nums[mid];
15 }else if(left >= 1 && left+11] && nums[left] < nums[left+1])
16 {
17 return nums[left];
18 }else if(right >= 1 && right+11] && nums[right] < nums[right+1])
19 {
20 return nums[right];
21 }
22 else if(nums[mid] > nums[0])
23 {
24 left = mid + 1;
25 }else{
26 right = mid - 1;
27 }
28 }
29 return nums[0]1]?nums[0]:nums[nums.length-1];
30 }
31}
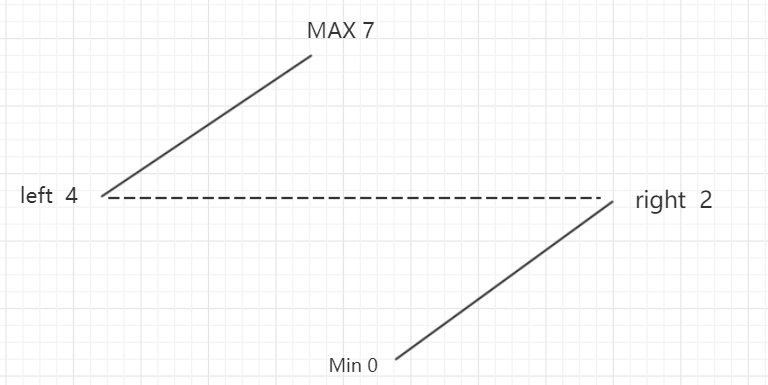
照例先举个例子。
对于数组[4,5,6,7,1,2,3],4,5,6,7为前半段,1,2,3位后半段,其中最小值是1,是我们要找的结果。
思路
如果这个旋转数组只有一个数直接返回这个数;
如果这个旋转数组的第一个数小于数组的最后一个数,那么说明旋转数组本身就是升序的,也就是说没有进行旋转,直接返回第一数;
而对于其他情况,采取二分查找的思想进行查找,当在二分的过程中,找到这样的一个数(这个数既比它的左边的数下,又比它右边的数小),那么就是最小的数直接返回即可;
如果在循环结束以后没有找到,说明肯定是在边界,因为最小值如果在中间,那么必然已经经过了判断直接返回了结果,所以这个时候只需要比较数组的第一个数和最后一个数。
详解
代码3-4行就是数组只有一个数的情况;
代码4-6行就是数组不是旋转数组,就是升序的,直接返回第一个数。接下来就是需要进行二分查找,数组是旋转数组。
12行到14行就是判断nums[mid]是不是最小的数,判断的方法就是和它的左右的两个数nums[mid+1].nums[mid-1]进行比较;
15-17行就是判断nums[left]是不是最小的数;
18-20行就是判断nums[right]是不是最小的数;
接下当12-20行代码判断都不为真,也就是说还没有找到这样的最小的数,进入到22行代码;
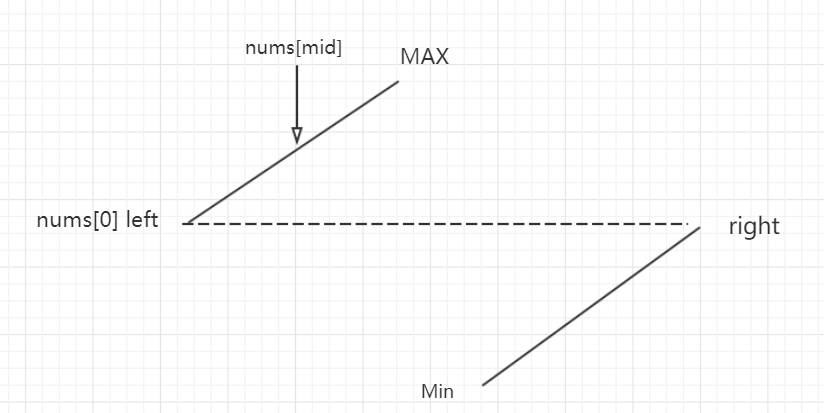
22行代码是nums[mid]>nums[0],这说明nums[mid]比nums[0]大,所以nums[mid]肯定在前半段,如下图所示。
这个时候观察图可知,为了找到Min,所以这时候需要令left = mid+1,去逼近图中的Min的值所在的位置。
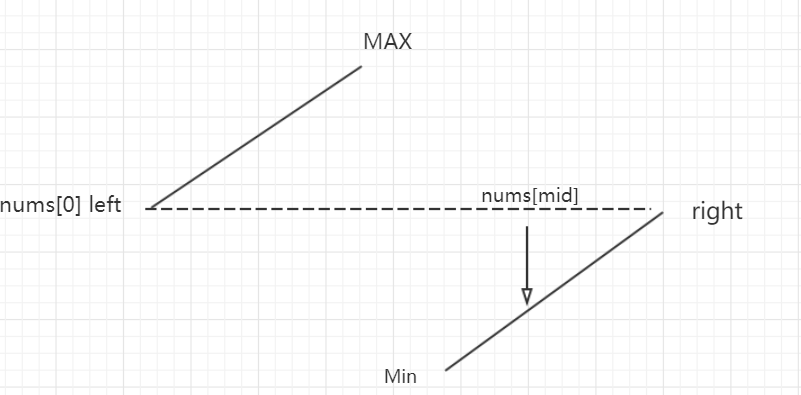
如果22行代码判断为假,进入25行代码,也就是nums[mid]
所以为了逼近Min值,应该去令right=mid-1;
当在while循环中重复的去执行上述的查找过程,要么就是找到了,直接返回了结果,程序结束;要么就是left>right,但是没有找到这样的最小值。
而没有找到这样的最小值,说明最小值不在数组的中间部分,在的话已经返回了呀,所以最小值只可能在数组的边界部分,也就是nums[0]和nums[nums.length-1],这个时候只需要比较二者的大小然后返回两者的最小值。也就是代码29行干的事情。
结束语
总体来说思路比较简单,今天就到这里~
END
推荐阅读
每天一道leetcode-81
每天一道leetcode-33
一个你值得关注的百度人的技术公众号
扫一扫
![]()
有福利