数据结构Collection-----Vector及其子类Stack源码解析

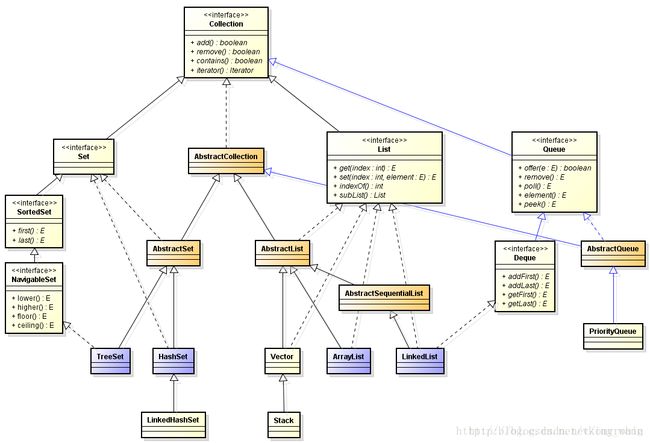
继承关系

通过图片我们能够看出Stack是Vector的子类，Stack就是常说的栈结构

Vector：重要的属性和构造方法

public class Vector<E> extends AbstractList<E> implements List<E>,
       RandomAccess, Cloneable, Serializable {

    /**
     * The number of elements or the size of the vector.
     * 数据元素数量
     */
    protected int elementCount;

    /**
     * The elements of the vector.
     * 底层实现Object数组
     */
    protected Object[] elementData;

    /**
     * How many elements should be added to the vector when it is detected that
     * it needs to grow to accommodate extra entries. If this value is zero or
     * negative the size will be doubled if an increase is needed.
     * 
     * 扩容因子，扩容量，稍后遇到的时候会介绍
     */
    protected int capacityIncrement;

    //默认数组长度
    private static final int DEFAULT_SIZE = 10;

    /**
     * Constructs a new vector using the default capacity.
     */
    public Vector() {
        this(DEFAULT_SIZE, 0);
    }

    /**
     * Constructs a new vector using the specified capacity.
     *
     * @param capacity
     *            the initial capacity of the new vector.
     * @throws IllegalArgumentException
     *             if {@code capacity} is negative.
     */
    public Vector(int capacity) {
        this(capacity, 0);
    }

    /**
     * Constructs a new vector using the specified capacity and capacity
     * increment.
     * 
     * 由于上面两个构造最终调用的都是这个构造函数，我们来看这个构造
     * 
     * @param capacity
     *            the initial capacity of the new vector.
     * @param capacityIncrement
     *            the amount to increase the capacity when this vector is full.
     * @throws IllegalArgumentException
     *             if {@code capacity} is negative.
     * 
     */
    public Vector(int capacity, int capacityIncrement) {
        //没什么好说的，设定数组长度必须大于0
        if (capacity < 0) {
            throw new IllegalArgumentException("capacity < 0: " + capacity);
        }
        //初始化数组、数据元素数量和扩容因子（注意这里有扩容因子的初始化操作，前两个构造默认值都是0）
        elementData = newElementArray(capacity);
        elementCount = 0;
        this.capacityIncrement = capacityIncrement;
    }

• 增加

@Override
public synchronized boolean add(E object) {
 //数据元素数量和数组数据量相等，说明数组容量不足需要扩容
    if (elementCount == elementData.length) {
        growByOne();
    }
    //数组的增加数据操作，相信都看的懂
    elementData[elementCount++] = object;
    //计数器++
    modCount++;
    return true;
}

//接下来我们看看扩容的时候发生了什么，这里就需要扩容因子这个变量了
private void growByOne() {
    int adding = 0;
    //判断扩容因子是否小于等于0，我们知道使用无参和1个参数构造的时候，都未指定扩容因子的大小，默认值就是0
    if (capacityIncrement <= 0) {
        //如果未指定capacityIncrement 的值，adding赋值为当前数组的长度，如果数组长度为0，那么
        //adding赋值为1
        if ((adding = elementData.length) == 0) {
            adding = 1;
        }
    } else {
        //如果指定了一个大于0的capacityIncrement ，adding赋值为capacityIncrement扩容因子值
        adding = capacityIncrement;
    }
    //重新构建一个数组，数组长度为elementData.length + adding
    //简单理解如果未指定capacityIncrement 的值，原容量*2（0的时候+1）
    //指定capacityIncrement 的值，原容量+capacityIncrement
    E[] newData = newElementArray(elementData.length + adding);
    System.arraycopy(elementData, 0, newData, 0, elementCount);
    elementData = newData;
}

@Override
public void add(int location, E object) {
    insertElementAt(object, location);
}

public synchronized void insertElementAt(E object, int location) {
    if (location >= 0 && location <= elementCount) {
        //扩容操作
        if (elementCount == elementData.length) {
            growByOne();
        }
        int count = elementCount - location;
        if (count > 0) {
            System.arraycopy(elementData, location, elementData,
                    location + 1, count);
        }
        elementData[location] = object;
        //数据元素数量++
        elementCount++;
        //计数器++
        modCount++;
    } else {
        throw arrayIndexOutOfBoundsException(location, elementCount);
    }
}

• 删除

/**
 * 没什么好说的，就是数组操作
 */
@SuppressWarnings("unchecked")
@Override
public synchronized E remove(int location) {
    if (location < elementCount) {
        E result = (E) elementData[location];
        elementCount--;
        int size = elementCount - location;
        if (size > 0) {
            System.arraycopy(elementData, location + 1, elementData,
                    location, size);
        }
        elementData[elementCount] = null;
        modCount++;
        return result;
    }
    throw arrayIndexOutOfBoundsException(location, elementCount);
}

• 修改

/**
 * 直接将数组location位置数据，数组操作替换
 */
@SuppressWarnings("unchecked")
@Override
public synchronized E set(int location, E object) {
    if (location < elementCount) {
        E result = (E) elementData[location];
        elementData[location] = object;
        return result;
    }
    throw arrayIndexOutOfBoundsException(location, elementCount);
}

• 查找

/**
 * 不想说话
 */
@Override
public E get(int location) {
    return elementAt(location);
}

@SuppressWarnings("unchecked")
public synchronized E elementAt(int location) {
    if (location < elementCount) {
        return (E) elementData[location];
    }
    throw arrayIndexOutOfBoundsException(location, elementCount);
}

总结：基本上除了扩容方式和ArrayList有所区别（可以根据capacityIncrement自行控制扩容数量），还有相关操作函数都带有synchronized 关键字外（线程安全），基本是类似的

Stack：重要的属性和构造方法

public class Stack<E> extends Vector<E> {
    /**
     * Constructs a stack with the default size of {@code Vector}.
     * 尴尬，没啥太重要的，Stack毕竟是继承自Vector
     */
    public Stack() {
    }
}

提到栈结构，我们不得不说栈中很重要的概念，出栈和入栈。

• 出栈

/**
 * Returns the element at the top of the stack and removes it.
 *  * @return the element at the top of the stack.
 * @throws EmptyStackException
 *             if the stack is empty.
 * @see #peek
 * @see #push
 */
@SuppressWarnings("unchecked")
public synchronized E pop() {
    //elementCount 继承自Vector的属性，如果是0抛出异常
    if (elementCount == 0) {
        throw new EmptyStackException();
    }
    //数据元素数量--
    final int index = --elementCount;
    //获取最后一个元素
    final E obj = (E) elementData[index];
    //将最后一个元素置空
    elementData[index] = null;
    //计数器++
    modCount++;
    return obj;
}

栈结构出栈就是置空栈顶（最后一个）元素，所以栈结构是一种后进先出的线性表结构也叫做LIFO（Last in First out）表
这里我们会发下一个很有趣的现象，这里并没有像Vector.remove元素的时候采取的重新构建数组的方式，而是只是将栈顶（最后一个）元素置空，这是为了什么呢，因为在栈中，出栈入栈是最基本也是最普遍的操作相对来说比较频繁，如果我每次出栈都要重新构建数组长度，重新分配内存，每次入栈的时候又要扩容，实在是太小家子气了！

• 入栈

/**
 * Pushes the specified object onto the top of the stack.
 *
 * @param object
 *            The object to be added on top of the stack.
 * @return the object argument.
 * @see #peek
 * @see #pop
 */
public E push(E object) {
    addElement(object);
    return object;
}

addElement是Vector中的方法，也就是Stack父类的方法

/**
 * Adds the specified object at the end of this vector.
 *  * @param object
 *            the object to add to the vector.
 */
public synchronized void addElement(E object) {
    //扩容操作，是不是很眼熟和Vector的add区别不大，但是这里需要注意的是，因为上文提到出栈操作中并没有将
    //elemetData数组像Vector.remove重新构建数组，所以elementData.length并没有发生变化，只不过出
    //栈的元素赋值为null了，所以elementCount表示的是非null元素的数量，只有在栈中非null元素数量和数
    //组长度相同时，才进行扩容操作，否则直接入栈进行类似set一样的修改操作，将null元素赋值
    if (elementCount == elementData.length) {
        growByOne();
    }
    elementData[elementCount++] = object;
    modCount++;
}

• 查找

/**
  * Returns the index of the first occurrence of the object, starting from
  * the top of the stack.
  *
  * @return the index of the first occurrence of the object, assuming that
  *         the topmost object on the stack has a distance of one.
  * @param o
  *            the object to be searched.
  */

 public synchronized int search(Object o) {
     final Object[] dumpArray = elementData;
     final int size = elementCount;
     if (o != null) {
         //从数组elementData的栈顶（elementData）开始查找，返回找到的第一个对象所在的下标位置
         for (int i = size - 1; i >= 0; i--) {
             if (o.equals(dumpArray[i])) {
                 return size - i;
             }
         }
     } else {
         for (int i = size - 1; i >= 0; i--) {
             if (dumpArray[i] == null) {
                 return size - i;
             }
         }
     }
     return -1;
 }

栈结构在查找元素的时候也是先从栈顶（最后一个）元素开始向栈底（第一个元素）进行遍历。

我们做Android都对Activity不陌生，Activity就是一个标准的使用栈这种数据结构来存储的，还有一种标准的栈结构，就是波兰表达式，也是后缀表达式，我们数学课堂上学的四则运算称之为中缀表达式，但是计算机是无法理解的，而计算机采用的就是后缀表达式来处理，而中缀向后缀的转换过程就使用的栈这种数据结构。

中缀表达式 ：
9+（3-1）*3+10/2 = 20

后缀表达式 ：
931-3*+10 2/+
923*+10 2/ +
96+10 2/ +
15 10 2/ +
15 5 +
20
具体如何转换的不在本章讨论范围，而且连表达式都是抄的，我就不班门弄斧了。