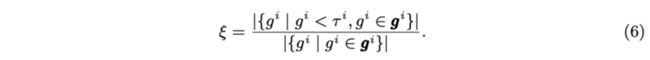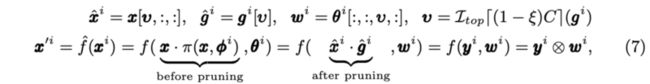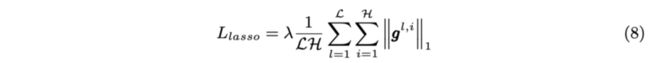近期,动态网络在加速推理这方面有很多研究,DGC(Dynamic Group Convolution)将动态网络的思想结合到分组卷积中,使得分组卷积在轻量化的同时能够加强表达能力,整体思路直接清晰,可作为网络设计时的一个不错的选择
来源:晓飞的算法工程笔记 公众号
论文: Dynamic Group Convolution for Accelerating Convolutional Neural Networks
Introduction
分组卷积目前广泛应用于轻量级网络中,但论文分析发现分组卷积有两个致命的缺点:
- 由于引入稀疏连接,减弱了卷积的表达能力,导致性能的降低,特别对于难样本。
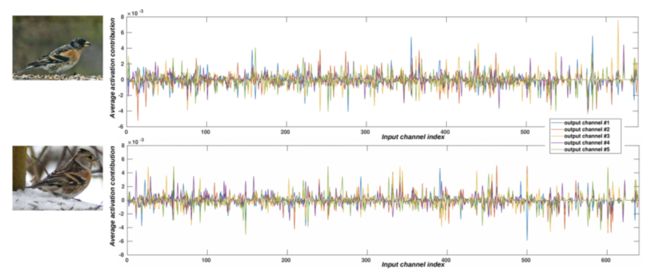
- 固定的连接模式,不会根据输入样本的特性而改变。而论文通过可视化DenseNet中间层的输入维度对输出维度的贡献发现,不同的输入维度对不同的输出的贡献是不一样的,而且这个贡献关系在不同的输入样本之间也存在差异。
参考动态网络的思想,论文提出动态分组卷积(DGC, dynamic group convolution),为每个分组引入小型特征选择器,根据输入特征的强度动态决定连接哪些输入维度,而多个分组能捕获输入图片中不同的互补特征,学习到丰富的特征表达能力。为此,动态分组卷积能够在保持原网络的完整结构下,自适应地为每个分组的选择最相关输入维度。
Group-wise Dynamic Execution
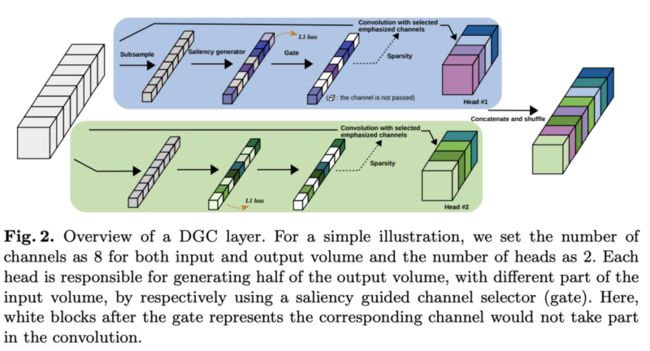
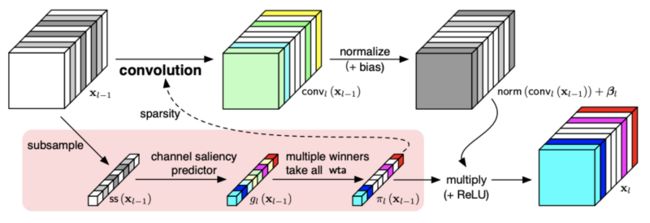
DGC的结构如图2所示,将输出维度分成多个分组,每组都配有辅助head,用来决定那些输入维度用于卷积计算。每个分组的逻辑如下:
- saliency generator生成输入维度的重要性分数。
- input channel selector采用gating策略根据重要性评分来动态决定输入维度最重要部分。
- 对选择的输入维度子集进行正常的卷积操作。
最后,将所有head的输出concate并打乱,送入后续的BN层和激活层。
Saliency Generator
saliency generator为每个输入维度指定一个分数用来表示其重要程度,每个head都有特定的saliency generator,用来引导不同的head使用不同的输入维度,从而增加特征的多样化表达。saliency generator遵循了SE block的设计,对于第$i$个head,重要性向量$g^i$的计算为:
$g^i\in \mathbb{R}^{1\times C}$代表输入维度的重要性向量,$(z)_+$代表ReLU激活,$p$将每个输入特征图缩小为单个标量,论文采用使用全局平均池化,$\beta^{i}$和$W^{i}$为可学习参数,$\beta^{i}$为偏置,$W^{i}$两部转换操作$\mathbb{R}^{1\times C}\mapsto \mathbb{R}^{1\times C/d}\mapsto \mathbb{R}^{1\times C}$,其中d为压缩比。这里的$x^{i}$为全部输入维度,即在每个head中,所有的输入维度都是候选。
Gating Strategy
在获得重要性向量后,下一步是决定当前head选择哪些输入维度参与后续的卷积操作,可以用head-wise阈值或network-wise阈值来过滤分数较低的输入特征。论文使用的是head-wise阈值,给定目标裁剪比例$\zeta$,第$i$个head的阈值$\tau^{i}$满足:
重要性分数有两个作用:1) 重要性分数小于阈值的将被去除 2) 剩余的维度会使用对应的重要性分数进行加权,得到加权特征$y^{i}\in \mathbb{R}^{(1-\zeta)C\times H\times W}$。假设head数量为$\mathcal{H}$,第$i$个head的卷积核为$w^{i}\subset \theta^{i}, \theta^{i} \in \mathbb{R}^{k\times k\times C\times \frac{C^{'}}{\mathcal{H}}}$,则对应的卷积计算为:
公式7其实就是将选择的特征和对应的权值选出来进行常规卷积计算,$\mathcal{I}_{top} \lceil k\rceil (z)$返回$z$中最大的$k$个元素的下标,输出$x^{'i}\in \mathbb{R}^{\frac{C^{'}}{\mathcal{H}}\times H^{'}\times W^{'}}$,$\otimes$为常规卷积。在DGC的最后,各输出会合并然后打乱,输出$x^{'}$。
为了让重要性分数尽量稀疏,引入lasso损失:
$\mathcal{L}$为DGC层数,$\lambda$为预设的超参数。
Computation Cost
卷积核大小为$k$的常规卷积MAC为$k^2C^{'}CH^{'}W^{'}$,而DGC中,每个head的saliency generator和卷积的MAC为$\frac{2C^2}{d}$和$k^2(1-\zeta)C\frac{C^{'}}{\mathcal{H}}H^{'}W^{'}$。所以DGC层的MAC相对于常规卷积的节省比例为:
head的数量$\mathcal{H}$几乎对整体的计算消耗没有影响。
Invariant to Scaling
DGC方法整体思想与动态剪枝算法FBS有点类似,FBS算法的流程如上图所示,计算的是输出维度的重要性分数,在最后的特征输出时使用重要性分数进行了加权,没有采用BN。这种加权方式会导致每个样本的特征分布差异较大,造成internal covariate shift问题。
而DGC虽然也使用重要性分数进行特征加权,但其对最后的卷积结果进行BN+ReLU归一化来避免这个问题:
Training DGC Networks
DGC网络从零开始训练,不需要预训练模型。在反向传播阶段,仅计算推理时选择的维度的相关权值的梯度,其它设为零。为了防止剪枝导致训练损失变化过大,在训练过程逐步增加裁剪比例$\zeta$。整体训练分为3个阶段,第一阶段(前1/12 epochs)用于warm up,第二阶段逐步提升剪裁比例进行训练,第三阶段(后1/4 epochs)用于fine-tune稀疏网络,学习率下降采用余弦退火下降方法。
Experiments
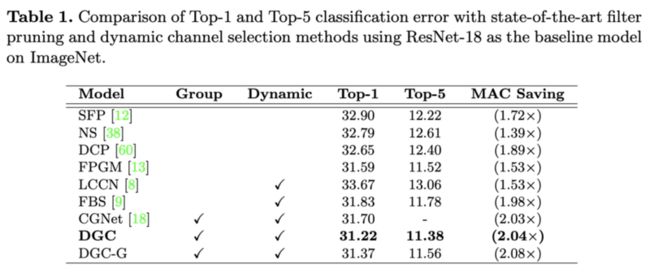
与剪枝方法和动态维度选择方法对比,DGC-G使用network-wise阈值进行维度选择,这个阈值是在训练中学习来的。
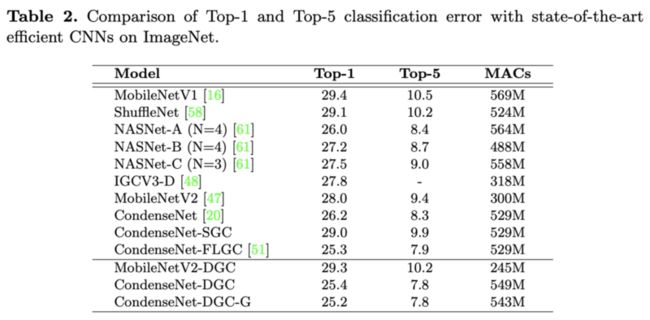
与其它轻量级网络对比。
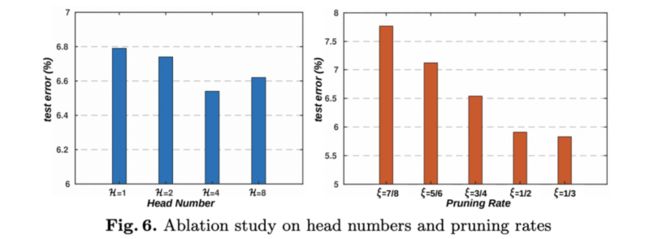
不同参数设置的性能对比。
可视化浅层和深层的重要性分数和过滤情况。
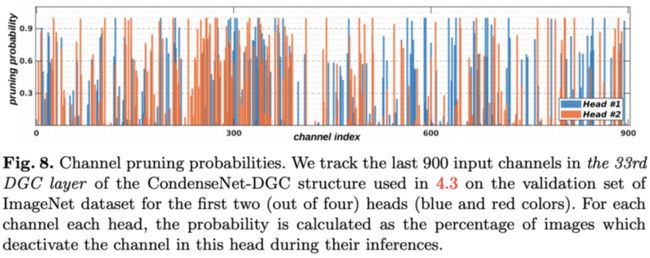
DGC网络某层的其中一个head对于各输入维度的裁剪概率。
Conclustion
DGC(Dynamic Group Convolution)将动态网络的思想结合到分组卷积中,使得分组卷积在轻量化的同时能够加强表达能力,整体思路直接清晰,可作为网络设计时的一个不错的选择。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
![]()