单调栈、单调队列和并查集

单调栈

单调栈，故名思意，就是栈内元素具有单调性的栈。可以是单调递增，也可以是单调递减，抑或是单调非增等。

步骤

单调栈的原理比较简单，只需要两步即可。以单调递增的单调栈为例：

• 如果栈为空，则将新元素入栈。
• 如果栈非空，比较要加入的元素与栈顶元素的大小
  • 如果大于栈顶元素，将新元素加入
  • 如果小于或等于栈顶元素，则不断弹出栈顶元素，直到栈顶元素小于新元素或栈为空，之后将新元素入栈。

可以结合一个例子来看：

比如有一个数列，[1,6,7,2,1,5,8,2,4],在这个数列中维护一个递增的栈，具体过程如下：

数列		1	6	7	2	1	5	8	2	4
栈内元素	$\varnothing$	1	1,6	1,6,7	1,2	1	1,5	1,5,8	1,2	1,2,4

• 刚开始栈为空，随后加入1
• 6比1大，所以6入栈
• 7比大，所以7入栈
• 2比7小，弹出栈顶元素7，栈顶元素为6
  • 2比6小，弹出栈顶元素6
  • 2比1大，2入栈
• 重复上述步骤

可以看出，每个元素最多入栈一次，出栈一次，时间复杂度$O(n)$

代码

#include 
#include 
using namespace std;
int main() {
    vector< int > array = {1,6,7,2,1,5,8,2,4};
    vector<int> Stack;
    for( auto i : array )
    {
        while( !Stack.empty() and Stack.back() >= i ) Stack.pop_back();
        Stack.push_back( i);
        //用于输出栈内元素
        for( auto j : Stack ) cout << j << " ";
        cout << endl;
    }
    return 0;
}

结果:

1
1 6
1 6 7
1 2
1
1 5
1 5 8
1 2
1 2 4

应用

适合解决要求在动态变化中维持单调性的问题。

以一个经典题目为例：n个矩形紧靠在一起，给定n个矩形的高度，在矩形内部找到一个面积最大的矩形。矩形的宽度均为1.类似下图：

那要怎么解决呢，分析问题可以知道，对于每一个矩形，可以由它构成的面积有两部分构成：本身的面积，以及以本身高度为矩形的高向后延申的可以构成最大矩形的面积(由于单调栈的性质，在自己之后的矩形高度一定高于自己)。在过程中动态计算这两部分值并记录过程中的最大值。
那么要怎么计算呢，可以维护一个单调递增的单调栈。相当于把原来的矩形替换成这个延申的矩形。每当一个矩形出栈的时候，计算当前矩形的向后延申可以构成的最大面积。在入栈的时候，将宽度定义为他可以向前延申的最长宽度，因为高于他的部分已经不会再对答案做出贡献了。
具体过程如图，下标分别表示矩形的高和宽，为了方便实现，可以人为的在最后添加一个高度为0的矩形。

步骤	计算需要计算的面积	此步骤过后栈内元素
step1	无
step2
step3	无
step4	无
step5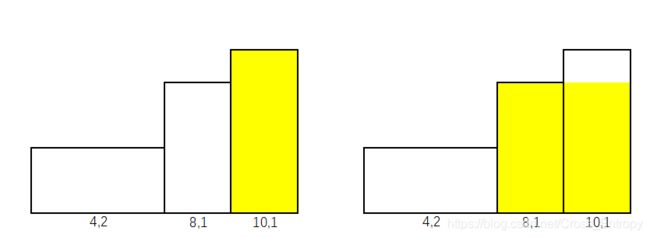
step6
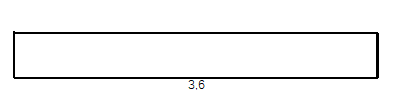step7		无

#include 
#include 
#include 
using namespace std;
struct node
{
    long long height, weight;
    node() {}
    node( long long height, long long weight ) : height(height), weight(weight) {}
};
int main()
{
    int n;
    while( scanf("%d", &n), n )
    {
        long long ans = 0; vector< node > v;
        for( int i = 0; i <= n; ++ i )
        {
            long long height;
            if( i == n ) height = 0; else scanf("%lld", &height);
            int len = 0;
            while( !v.empty() and height <= v.back().height )
            {
                len += v.back().weight;
                ans = max( ans, v.back().height * len );
                v.pop_back();
            }
            v.push_back( node( height, len + 1 ) );
        }
        cout << ans << endl;
    }
    return 0;
}

单调队列

单调队列，即在队列中维护单调性，通常使用双端队列。常用来求解在某个固定区间内的最值问题，如典型的滑动窗口问题——给定数列，求解对于任意i，[i,i-3]范围内的最小值。

步骤

利用双端队列和单调栈的思想，以寻找最小值的滑动窗口为例，具体过程如下：

当遇到一个新的元素

• 检查队首是否有元素需要退出队列(即在当前窗口外)。如果有则出队。
• 比较当前元素和队尾元素的大小
  • 如果当前元素大于或等于队尾元素，则从队尾入队。
  • 如果当前元素小于队尾元素，则不断弹出队尾元素，直到当前元素大于或等于队尾元素(因为当前元素比队尾元素更小，所以队列中比当前元素大的那些，一定不会成为答案)

可以看出，每个元素最多入队一次出队一次，时间复杂度$O(n)$

举个例子，比如数列[ 1, -2, 3, -2, 6, 2, 9, 5, 10 ]，对任意i，寻找[i,i-2]内(窗口大小为3)的最小值。

数列	1	-2	3	-2	6	2	9	5	10
窗口中的元素	1	1，-2	1,-2,3	-2,3,-2	3,-2,6	-2,6,2	6,2,9	2,9,5	9,5,10
队列中的元素	1	-2	-2,3	-2,-2	-2,6	-2,2	2,9	2,5	5,10
最小值	1	-2	-2	-2	-2	-2	2	2	5

代码

正如例子中看到的，为了判断队首元素是否需要出队，需要使用结构体保存位置信息。

#include 
#include 
#include 
using namespace std;
struct node
{
    int value, pos;
    node(){}
    node( int value, int pos ):value(value), pos(pos) {}
};
int main()
{

    vector< int > array = { 1, -2, 3, -2, 6, 2, 9, 5, 10 };
    int k = 3; //窗口大小
    deque< node > que;
    for( int i = 0; i < array.size(); ++ i )
    {
        while( !que.empty() and i - que.front().pos >= k ) que.pop_front();
        while( !que.empty() and array[i] < que.back().value  ) que.pop_back();
        que.push_back( { array[i], i});
        //输出当前元素以及当前元素前面k-1个元素的最小值
        cout << que.front().value << " ";
    }
    return 0;
}

结果：

1 -2 -2 -2 -2 -2 2 2 5

应用

类似上面的例子，即某个区间的最值问题。

并查集

并查集主要用来解决分类或划分类的问题。比如，一幅图上有多少连通块；给定一部分人的家庭关系，问一共有多少个家族等等。

步骤

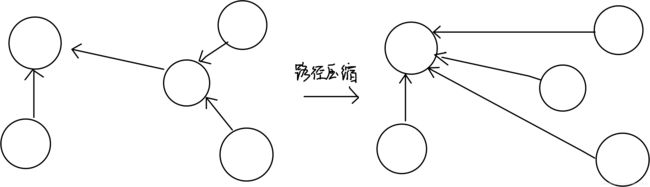
最原始的想法是，每个节点记录其父节点。但事实上，每次查询都会回归到根节点，造成时间的浪费，所以通常采取路径压缩的做法，并使用递归的方式实现。

• 如果当前节点的父节点是自己(即为根)，则返回父节点
• 否则，当前节点的父节点等于父节点的父节点。找到根后，讲当前节点的父节点替换成根节点来实现路径压缩。

可以看出所谓路径压缩，就是指的如下操作：

代码

寻找根节点：

int fa[maxn];
int GetFa( int x )
{
    if( x == fa[x] ) return x;
    fa[x] = GetFa(fa[x]);
    return fa[x];
}

连接两个节点：

void Merge( int x, int y )
{
    int u = GetFather(x), v = GetFather(y);
    if( u != v ) father[v] = u;
    return;
}

应用

即求解分类问题。
在实际使用时，有时候还需要额外维护一些其他的信息或者合并方式具有一定的规则。这种并查集被称为带权并查集。