各类平衡树的学习（一）——Splay

一.一道模板题.
题目：BZOJ3224.
题目大意：在序列上维护一个数据结构支持：
1.插入数$x$.
2.删除数$x$（只删一个）.
3.查找$x$的最小排名.
4.查找排名为$x$的数.
5.查找$x$的前驱.
6.查找$x$的后继.
$1\le n\le 10^5$.

虽然在《各类平衡树的学习（零）——二叉搜索树BST》（建议先去看看）中我们用二叉搜索树来做了下这道题，但这种裸题一般都会卡掉一般的二叉搜索树，所以我们现在需要用到平衡树来维护.

平衡树就是利用一些机制，使得每一次的操作效率是$O(\log n)$或者是均摊$O(\log n)$的二叉查找树，常见的平衡树有Treap、Splay、Red-Black Tree、替罪羊树、Size-Balanced Tree、AVL、Leafy Tree等.

在上述的常见的平衡树中，Splay和Treap在OI中较为常用，且功能强大，这里我们就来介绍一下Splay实现各类操作.


二.splay维护的信息与建树.

splay树只需要在普通BST的基础上多存一个父亲指针$fa$，而且建树与普通BST一模一样，下面直接给出代码：

struct tree{
  int x,fa,s[2],siz,cnt;
}tr[N+9];
int cn,rot;

void Pushup(int k){tr[k].siz=tr[tr[k].s[0]].siz+tr[tr[k].s[1]].siz+tr[k].cnt;}

int New_node(int x,int fa){
  tr[++cn]=tree();
  tr[cn].x=x;tr[cn].siz=tr[cn].cnt=1;
  tr[cn].fa=fa;if (fa) tr[fa].s[x>tr[fa].x]=cn;
  return cn;
}

void Build(){cn=0;rot=New_node(-INF,0);New_node(INF,1);Pushup(1);}

三.旋转操作Rotate.

旋转是指把两个节点$x$和$x$的父亲$y$的父子关系改变，即让$x$成为$y$，且不破坏原树的二叉查找树性质.

这个过程可以用下面的图来表示：

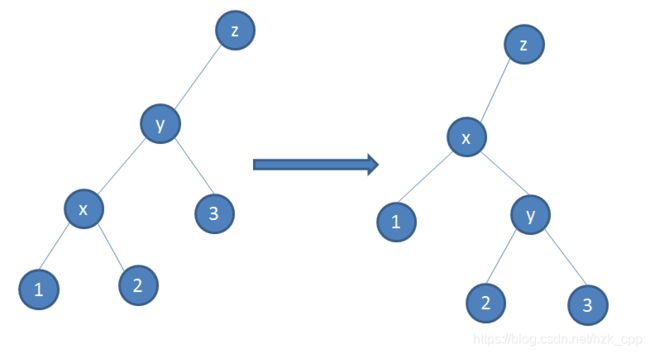
那么我们来设计这个旋转函数吧！

首先我们考虑它们在旋转前的关系，$tr[x].fa=y,tr[y].fa=z$.深入探究它们的关系，设$k=tr[y].s[1]==x$，即$tr[y].s[k]=x$，那么$tr[x].s[k]=1,tr[x].s[kxor1]=2,tr[y].s[kxor1]=3$.

考虑把它们旋转后的关系，发生改变的只有$tr[z].s[tr[z].s[1]==y]=x,tr[y].s[k]=2,tr[x].s[kxor1]=x$，所以我们可以写出这样的代码：

void Rotate(int x){
  int y=tr[x].fa,z=tr[y].fa,k=tr[y].s[1]==x;
  if (z) tr[z].s[tr[z].s[1]==y]=x;tr[x].fa=z;
  tr[y].s[k]=tr[x].s[k^1];if (tr[x].s[k^1]) tr[tr[x].s[k^1]].fa=y;
  tr[x].s[k^1]=y;tr[y].fa=x;
  Pushup(y);Pushup(x);
}

当然也有一种写法是把Roatate操作分为左旋（$x<y$）和右旋（$x>y$）来写的，貌似这样效率会更高，但同时代码也会更长.


四.伸展操作Splay.

Splay操作是splay的核心，它的功能是在不改变树的中序遍历的情况下，把某个节点移到目标节点（通常是根或根的某个儿子）儿子的位置.

具体实现很简单，因为目标节点通常为根或根的儿子，所以只需要把$x$节点不断往上旋转直到$x$成为了指定节点的儿子.

具体代码如下：

void Splay(int x,int go){
  for (;tr[x].fa^go;Rotate(x));
  if (!go) rot=x;
  Pushup(x);      //一定要Pushup
}

但是这样的Splay有可能会TLE，这是因为没有时间复杂度保证，它可以被这样一种数据卡掉：

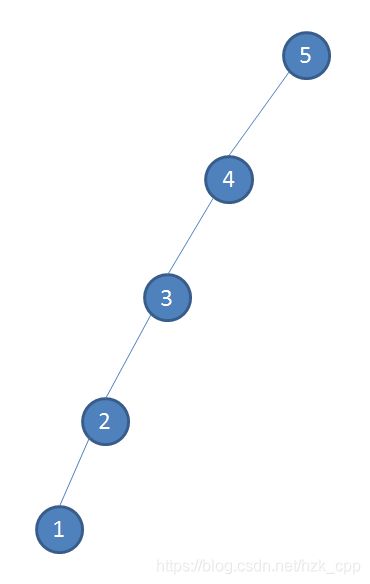
这个时候我们只需要不断查询$1,5,1,5,1,5,...$就可以让时间复杂度退化成一次查询$O(n)$.

那么我们该如何让时间复杂度变得有保证呢？考虑两种情况：

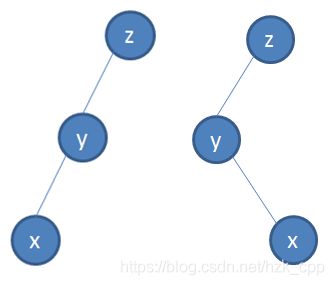
第一种情况时，$x,y$和$y,z$的父子关系相同，那么我们就先旋转$y$，再旋转$x$；而第二种情况时，$x,y$和$y,z$的父子关系不同，就直接两次旋转$x$即可.

代码如下：

void Splay(int x,int go){
  int y,z;
  while (tr[x].fa^go){
  	y=tr[x].fa;z=tr[y].fa;
  	if (z) tr[y].s[0]==x^tr[z].s[0]==y?Rotate(x):Rotate(y);
  	Rotate(x);
  }
  if (!go) rot=x;
  Pushup(x);      //一定要Pushup
}

然后我们就能保证一次操作时间复杂度为$O(\log n)$啦！至于证明在最后…


五.一些与BST差别不大的操作.

splay上所有操作的实现可以写成与BST一模一样，但是为了保证平衡，对于我们使用过的所有从根到一个节点$k$的链都需要$Splay(k,0)$以保证复杂度.

由于查询前驱后继与删除的代码可以通过splay这个操作写的更加简洁，所以这里先奉上其它几个操作的代码：

int Find_val(int x){
  int k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x]);
  Splay(k?k:fa,0);
  return k?k:-1; 
}

int Insert(int x){
  int k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x]);
  k?++tr[k].cnt:k=New_node(x,fa);
  Splay(k,0);
  return k;
}

int Query_rank(int x){
  int res=0,k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x])
    if (x>tr[k].x) res+=tr[k].cnt+tr[tr[k].s[0]].siz;
  if (k) res+=tr[tr[k].s[0]].siz;
  Splay(k?k:fa,0);
  return res;
}

int Find_rank(int p){
  ++p;
  int k=rot;
  while (2333)
    if (p>tr[tr[k].s[0]].siz+tr[k].cnt) p-=tr[tr[k].s[0]].siz+tr[k].cnt,k=tr[k].s[1];
    else if (p<=tr[tr[k].s[0]].siz) k=tr[k].s[0];
      else break;
  Splay(k,0);
  return k;
}

六.简化前驱与后继的代码.

我们发现若直接用写BST的方式写有些长，考虑是否可以利用splay的先天优势来简化代码呢？

考虑一下上一块中$Find\_val(x)$的作用，若$x$存在，很明显$x$会被提到根，并且$x$的前驱和后继只需要一个简单的迭代就可以实现了；若$x$不存在，则被提到根的节点有可能是$x$的前驱或后继，这个时候我们需要判定一下是前驱还是后继，另外一个也可以通过简单的迭代实现了.

代码如下：

int Lower(int x){
  Find_val(x);
  int k=rot;
  if (tr[k].x<x) return k;
  for (k=tr[k].s[0];tr[k].s[1];k=tr[k].s[1]);
  Splay(k,0);
  return k;
}

int Upper(int x){
  Find_val(x);
  int k=rot;
  if (tr[k].x>x) return k;
  for (k=tr[k].s[1];tr[k].s[0];k=tr[k].s[0]);
  Splay(k,0);
  return k;
}

七.简化删除的代码.

我们发现BST的删除又臭又长，而且调用的链难以处理，所以考虑简化一下代码.

同样的，$Find\_val(x)$使得键值为$x$的节点到了根的地方，若我们要移除根，可以找到$x$的前驱或后继移到根，再把$x$移到根儿子的位置，然后就可以直接删除了.

代码如下：

void Erase(int x){
  int k=Find_val(x);
  if (k==-1) return;
  --tr[k].cnt;
  if (tr[k].cnt<0) tr[k].cnt=0;
  if (tr[k].cnt) return;
  int nxt=Upper(tr[k].x);
  Splay(k,nxt);
  tr[nxt].s[0]=tr[k].s[0];if (tr[k].s[0]) tr[tr[k].s[0]].fa=nxt;
  Pushup(nxt);
}

八.通过前驱后继写插入删除.

其实插入删除还可以通过前驱后继写得十分简单.

对于插入$x$，我们可以先把$x$的前驱节点$l$和后继节点$r$找到，然后把$l$ Splay到根，$r$ Splay到$l$下面，然后$r$的右儿子就可以直接插入$x$了…

同理，删除$x$只需要把插入到$r$的右儿子改成把$r$的右儿子设成$0$就可以了…

不过这样写的话常数会很大，所以不是很推荐这样写…

代码如下：

int Insert(int x){
  int l=Lower(x),r=Upper(x),k;
  Splay(l,0);Splay(r,l);
  k=tr[r].s[0];
  k?++tr[k].cnt:k=New_node(x,r);
  Splay(k,0);
  return k;
}

void Erase(int x){
  int l=Lower(x),r=Upper(x),k;
  Splay(l,0);Splay(r,l);
  k=tr[r].s[0];
  if (!k) return;
  --tr[k].cnt;
  if (tr[k].cnt<0) tr[k].cnt=0;
  if (tr[k].cnt) Splay(k,0);
  else tr[r].s[0]=0,Splay(r,0);
}

九.完整代码.

普通平衡树代码如下：

//不用前驱后继简化插入删除
#include
  using namespace std;

#define Abigail inline void
typedef long long LL;

const int N=100000,INF=(1<<31)-1;

struct tree{
  int x,fa,s[2],siz,cnt;
}tr[N+9];
int cn,rot;

void Pushup(int k){tr[k].siz=tr[tr[k].s[0]].siz+tr[tr[k].s[1]].siz+tr[k].cnt;}

void Rotate(int x){
  int y=tr[x].fa,z=tr[y].fa,k=tr[y].s[1]==x;
  if (z) tr[z].s[tr[z].s[1]==y]=x;tr[x].fa=z;
  tr[y].s[k]=tr[x].s[k^1];if (tr[x].s[k^1]) tr[tr[x].s[k^1]].fa=y;
  tr[x].s[k^1]=y;tr[y].fa=x;
  Pushup(y);Pushup(x);
}

void Splay(int x,int go){
  for (int y,z;tr[x].fa^go;Rotate(x)){
    y=tr[x].fa;z=tr[y].fa;
    if (z^go) tr[z].s[0]==y^tr[y].s[0]==x?Rotate(x):Rotate(y);
  }
  if (!go) rot=x;
  Pushup(x);
}

int New_node(int x,int fa){
  tr[++cn]=tree();
  tr[cn].x=x;tr[cn].siz=tr[cn].cnt=1;
  tr[cn].fa=fa;if (fa) tr[fa].s[x>tr[fa].x]=cn;
  return cn;
}

void Build(){cn=0;rot=New_node(-INF,0);New_node(INF,1);Pushup(1);}

int Find_val(int x){
  int k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x]);
  Splay(k?k:fa,0);
  return k?k:-1; 
}

int Insert(int x){
  int k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x]);
  k?++tr[k].cnt:k=New_node(x,fa);
  Splay(k,0);
  return k;
}

int Query_rank(int x){
  int res=0,k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x])
    if (x>tr[k].x) res+=tr[k].cnt+tr[tr[k].s[0]].siz;
  if (k) res+=tr[tr[k].s[0]].siz;
  Splay(k?k:fa,0);
  return res;
}

int Find_rank(int p){
  ++p;
  int k=rot;
  while (2333)
    if (p>tr[tr[k].s[0]].siz+tr[k].cnt) p-=tr[tr[k].s[0]].siz+tr[k].cnt,k=tr[k].s[1];
    else if (p<=tr[tr[k].s[0]].siz) k=tr[k].s[0];
      else break;
  Splay(k,0);
  return k;
}

int Lower(int x){
  Find_val(x);
  int k=rot;
  if (tr[k].x<x) return k;
  for (k=tr[k].s[0];tr[k].s[1];k=tr[k].s[1]);
  Splay(k,0);
  return k;
}

int Upper(int x){
  Find_val(x);
  int k=rot;
  if (tr[k].x>x) return k;
  for (k=tr[k].s[1];tr[k].s[0];k=tr[k].s[0]);
  Splay(k,0);
  return k;
}

void Erase(int x){
  int k=Find_val(x);
  if (k==-1) return;
  --tr[k].cnt;
  if (tr[k].cnt<0) tr[k].cnt=0;
  if (tr[k].cnt) return;
  int nxt=Upper(tr[k].x);
  Splay(k,nxt);
  tr[nxt].s[0]=tr[k].s[0];if (tr[k].s[0]) tr[tr[k].s[0]].fa=nxt;
  Pushup(nxt);
}

Abigail getans(){
  int opt,x,n;
  scanf("%d",&n);
  Build();
  while (n--){
  	scanf("%d%d",&opt,&x);
  	switch (opt){
  	  case 1:
  	  	Insert(x);
  	  	break;
  	  case 2:
  	    Erase(x);
  	  	break;
  	  case 3:
  	  	printf("%d\n",Query_rank(x));
  	  	break;
  	  case 4:
  	  	printf("%d\n",tr[Find_rank(x)].x);
  	  	break;
  	  case 5:
  	  	printf("%d\n",tr[Lower(x)].x);
  	  	break;
  	  case 6:
  	    printf("%d\n",tr[Upper(x)].x);
  	  	break;
  	}
  }
}

int main(){
  getans();
  return 0;
}

//用前驱后继简化插入删除
#include
  using namespace std;

#define Abigail inline void
typedef long long LL;

const int N=100000,INF=(1<<31)-1;

struct tree{
  int x,fa,s[2],siz,cnt;
}tr[N+9];
int cn,rot;

void Pushup(int k){tr[k].siz=tr[tr[k].s[0]].siz+tr[tr[k].s[1]].siz+tr[k].cnt;}

void Rotate(int x){
  int y=tr[x].fa,z=tr[y].fa,k=tr[y].s[1]==x;
  if (z) tr[z].s[tr[z].s[1]==y]=x;tr[x].fa=z;
  tr[y].s[k]=tr[x].s[k^1];if (tr[x].s[k^1]) tr[tr[x].s[k^1]].fa=y;
  tr[x].s[k^1]=y;tr[y].fa=x;
  Pushup(y);Pushup(x);
}

void Splay(int x,int go){
  for (int y,z;tr[x].fa^go;Rotate(x)){
    y=tr[x].fa;z=tr[y].fa;
    if (z^go) tr[z].s[0]==y^tr[y].s[0]==x?Rotate(x):Rotate(y);
  }
  if (!go) rot=x;
  Pushup(x);
}

int New_node(int x,int fa){
  tr[++cn]=tree();
  tr[cn].x=x;tr[cn].siz=tr[cn].cnt=1;
  tr[cn].fa=fa;if (fa) tr[fa].s[x>tr[fa].x]=cn;
  return cn;
}

void Build(){cn=0;rot=New_node(-INF,0);New_node(INF,1);Pushup(1);}

int Find_val(int x){
  int k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x]);
  Splay(k?k:fa,0);
  return k?k:-1; 
}

int Query_rank(int x){
  int res=0,k=rot,fa=0;
  for (;k&&tr[k].x^x;fa=k,k=tr[k].s[x>tr[k].x])
    if (x>tr[k].x) res+=tr[k].cnt+tr[tr[k].s[0]].siz;
  if (k) res+=tr[tr[k].s[0]].siz;
  Splay(k?k:fa,0);
  return res;
}

int Find_rank(int p){
  ++p;
  int k=rot;
  while (2333)
    if (p>tr[tr[k].s[0]].siz+tr[k].cnt) p-=tr[tr[k].s[0]].siz+tr[k].cnt,k=tr[k].s[1];
    else if (p<=tr[tr[k].s[0]].siz) k=tr[k].s[0];
      else break;
  Splay(k,0);
  return k;
}

int Lower(int x){
  Find_val(x);
  int k=rot;
  if (tr[k].x<x) return k;
  for (k=tr[k].s[0];tr[k].s[1];k=tr[k].s[1]);
  Splay(k,0);
  return k;
}

int Upper(int x){
  Find_val(x);
  int k=rot;
  if (tr[k].x>x) return k;
  for (k=tr[k].s[1];tr[k].s[0];k=tr[k].s[0]);
  Splay(k,0);
  return k;
}

int Insert(int x){
  int l=Lower(x),r=Upper(x),k;
  Splay(l,0);Splay(r,l);
  k=tr[r].s[0];
  k?++tr[k].cnt:k=New_node(x,r);
  Splay(k,0);
  return k;
}

void Erase(int x){
  int l=Lower(x),r=Upper(x),k;
  Splay(l,0);Splay(r,l);
  k=tr[r].s[0];
  if (!k) return;
  --tr[k].cnt;
  if (tr[k].cnt<0) tr[k].cnt=0;
  if (tr[k].cnt) Splay(k,0);
  else tr[r].s[0]=0,Splay(r,0);
}

Abigail getans(){
  int opt,x,n;
  scanf("%d",&n);
  Build();
  while (n--){
  	scanf("%d%d",&opt,&x);
  	switch (opt){
  	  case 1:
  	  	Insert(x);
  	  	break;
  	  case 2:
  	    Erase(x);
  	  	break;
  	  case 3:
  	  	printf("%d\n",Query_rank(x));
  	  	break;
  	  case 4:
  	  	printf("%d\n",tr[Find_rank(x)].x);
  	  	break;
  	  case 5:
  	  	printf("%d\n",tr[Lower(x)].x);
  	  	break;
  	  case 6:
  	    printf("%d\n",tr[Upper(x)].x);
  	  	break;
  	}
  }
}

int main(){
  getans();
  return 0;
}

十.时间复杂度分析.

splay的具体如何用严谨的势能法分析我还不会，但是可以写一下主要的思想.

显然造成一棵BST不平衡的节点必然只有一种节点——只有一个儿子的节点.

而splay一次双旋的作用效果是什么？就是破坏掉这种节点.

再来考虑每次构造这种节点必然需要$O(1)$个操作，破坏这种节点必然只需要$O(1)$次splay也就是$O(\log n)$的复杂度，而操作次数只有$n$次，所以复杂度是$O(n\log n)$的.