后缀自动机学习笔记
学了一周后缀自动机,觉得...好难啊(主要还是自己太弱了...)
看见网上很多大佬的讲解,感觉总是有些似懂非懂,索性一起拿出来做一个总结,可能效果会好一些
首先,我们能看到这样一个定义:
后缀自动机是一个的确定性有限状态自动机,能接受这个字符串的所有后缀
然后就不知道了......
(不得不承认,对于我这种蒟蒻,看到这个定义的第一反应是看看别的...)
所以我们直接从后缀自动机的结构与性质入手
后缀自动机是一个有向无环图(这是第一个要点!!!因为大部分的字符串自动机都是树形结构,但这里不是!!!)
那么,后缀自动机上的点代表着什么呢?
一个后缀自动机上的点是一个压缩节点,它代表这一个字符串!
举个例子:
(以下的模板串均为abbab)
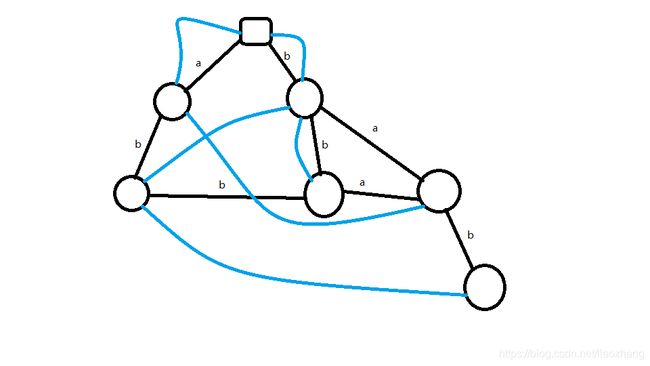
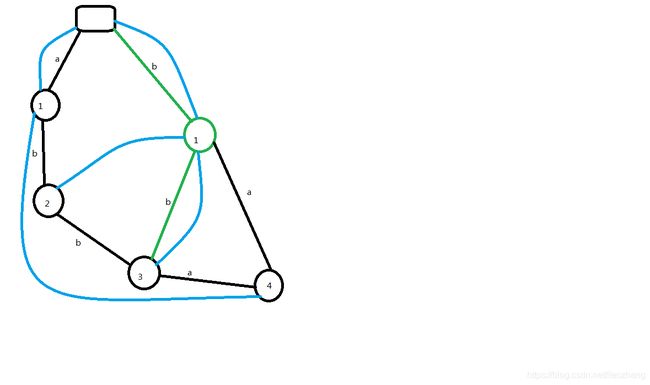
这是一个建好的后缀自动机
(不要介意它的长相,我们一会介绍如何构造)
那么我们看一下,如果我们真正插入所有后缀,那么这里的时间和空间都是无法接受的O(n^2)级别
所以我们需要将后缀进行压缩,压缩后即得到上图
(这里有一个吐槽:虽然这个东西叫“后缀”自动机,但是其大部分原理更接近于一个字符串的子串是一个前缀的后缀,所以或许“前缀”自动机这个名字更合适?)
可能你并没有理解,我们举个例子:
比如对于后缀“bbab“和“abbab”,如果我们按照传统的方式建立后缀树的话,那么我们需要建立9个节点
但是,我们发现,这两个后缀后3个字母是一样的(其实严格意义上,后4个字母都一样,但我们为了能从根节点识别到这个后缀,所以我们要单独提出第一个字符,这里在下面构造的时候有一个很重要的讨论,先留下)
因此,我们完全没有必要建立那么多节点,而是直接将节点b剩下的部分指向ab以下已经建好的部分,这样就实现了压缩空间!
而蓝色的线,我们把它叫做pre指针,它指向的是当前节点对应字符串的最长后缀对应的节点
它是非常有用的,这个作用会在应用中具体体现
接下来我们谈一谈构造:
后缀自动机的构造方式称为增量构造法,也即在一个已经构造好的后缀自动机上去增加一个字符,看看会发生什么
接下来开始构造
首先,我们在根节点上插入第一个节点a
情况大概是这个样子
蓝色的线即为pre指针,很显然,这里最长后缀并没有对应的节点,所以直接指回根节点
注意第一个节点上的标号,它并不是节点编号,而是一个叫len的量,具体含义及作用下面会谈到。
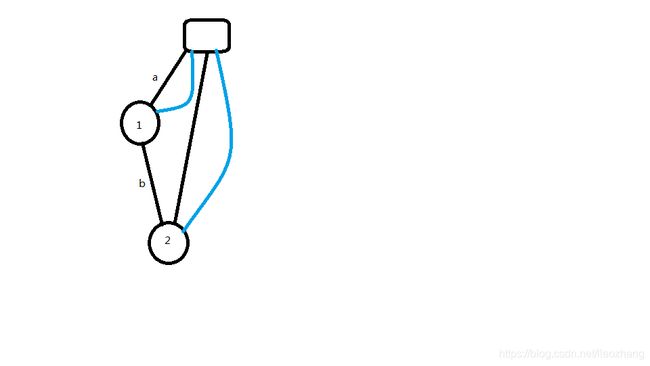
然后我们插入第二个节点:
大概就是这个样子
注意到由于ab最长后缀也找不到,所以pre同样指回根节点,而考虑到b也是一个后缀的开头,所以要补全根节点到b的出边
然后插入第三个节点
但是,这样做是否存在问题呢?
为了探究这个问题,首先我们要思考:前两个节点的pre指针是如何构造出来的?
虽然在图上直接找看似一目了然,但是真正实现并不容易!
具体的方法是,我们顺着上次插入的节点的pre指针一路向上跳,对跳到的每个节点,将它的对应指针指向这个新来的点。
具体解释一下:我们顺着pre指针向上跳的时候,跳到的每个点对应的都是这个字符串的一个后缀,同时他也在整个串中作为一个前缀出现过,所以我在新引进了一个字符以后,等价于在原有后缀后面加入了一个字符,自然也就等价于在这个串的最长后缀的后面加一个字符,也就是补全了儿子指针
可能文字并不清楚,我们给出一个具体例子:
比如串abac,已经插入了aba,那么可以看到,这个串的最长后缀(能连出pre指针的)应当是a
那么,如果我们继续插入一个c,那么得到的新串一定有一个后缀是ac(这里很显然)
那么出于压缩空间的考虑,我们可以直接由pre指针指向的那个a向新来的c连边,这样就可以直接从根开始识别后缀了
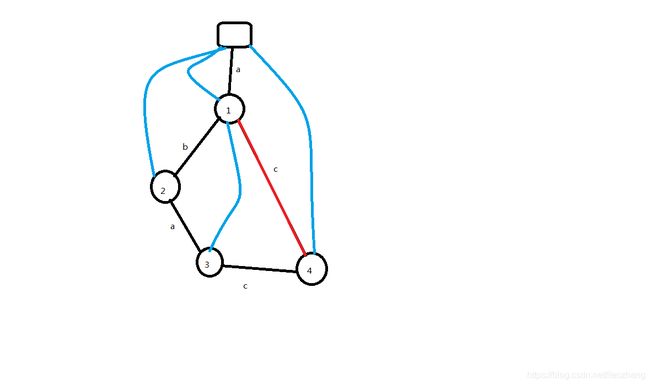
如果画出图大概就是这样:
可以看到,涂成红色的线就是我所提到的情况,直接从第一个a引出一条c边构成后缀ac
所以这里会有一个处理的操作
于是就涉及到了几个新的问题:
第一,如果顺着pre指针向上跳的时候,我们没有找到任何一个节点有与新来的节点相同的出边,那么这时很好处理,仅需将新来的节点pre指针指向根节点即可。
就像这个图,由于顺着a的pre指针向上跳的时候没有任何一个节点有出边b,所以直接将新节点的pre指针指向根节点即可。
第二,也是比较复杂的情况:如果跳到的某个节点竟然有相同的出边,这该怎么办?
就比如这种情况,我们顺着第一个b的pre指针向上跳的时候竟然惊喜的发现,它的pre指针有一个节点b!!!
这咋办?
基于朴素的思想,我们可以直接将新节点的pre指针指向那个节点b,就像上图给出的那样。
可是回到最初的问题:这样做合理吗?
很容易可以发现: 不合理!
为什么?
这时就体现出了上面提到的len变量的作用:我们看到,原先的b节点是一个压缩节点,考虑他的len并不等于他pre指针的len+1,也就意味着从他的pre指针到他之间压缩了信息!
(具体可以理解成压缩了ab和b两个串)
而当我们插入一个新节点以后,基于定义:pre指针指向了它所对应字符串的最长后缀
可...等等,这个最长后缀是哪一个呢?
是b,还是ab?
由于指向的b是一个压缩节点,所以我根本无法得知这个最长后缀是谁啊!
这也就产生了信息的丢失和混乱
所以我们直接这样去操作是不合理的
那怎么办?
可以看到,指向的b是压缩节点的原因就体现在len的关系上,由于b的len不等于它的pre的len+1,这意味着状态的压缩,也就意味着直接插入会导致信息的丢失
那么我们换一个思想:如果b的len等于他pre的len+1会怎样?
不难看出,此时直接连接pre指针就是合理的了!
因为此时可以说明中间没有压缩节点,也就是说在走后缀的时候是不会产生上面说的问题的了!
那么我们仿照这种思想,如果我将压缩节点展开,不就不会出现信息的丢失了吗?!
这就是后缀自动机构造中最为核心的一环!
回到上面的例子,那此时合理的做法应当是将b节点展开,构造一个新的b节点去接受pre指针
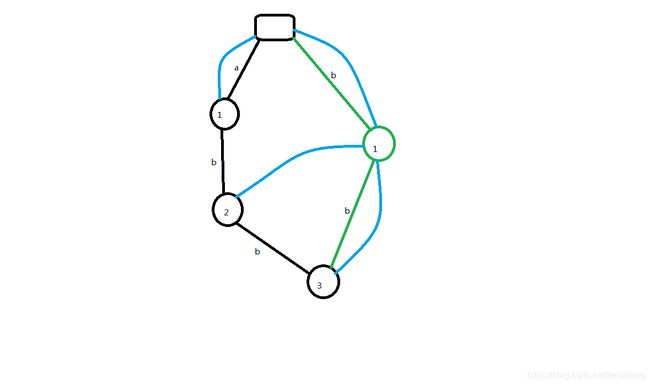
所以更合理的情况应当是这样:
其中用绿色给出了分裂出的节点
剩下的问题就好办了
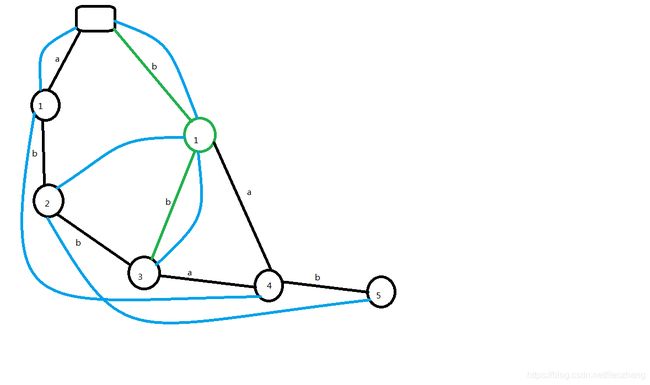
我们再插入一个节点:
可以看到,这就是我们上面提到的len恰好等于上一个len+1的情况,所以不需要分裂节点,只需建立pre指针即可。
再插入一个:
可以发现,这就是最开始我们画出来的那台后缀自动机了
所以我们的构造就完成了
贴个构造的代码
struct SAM
{
int tranc[27];
int len;
int pre;
int v;
int endpos;
}s[5000005];
int siz;
int las;
void ins(int c)
{
int nwp=++siz;
s[nwp].len=s[las].len+1;
s[nwp].endpos=1;
int lsp;
for(lsp=las;lsp&&!s[lsp].tranc[c];lsp=s[lsp].pre)s[lsp].tranc[c]=nwp;
if(!lsp)
{
s[nwp].pre=1;
}else
{
int lsq=s[lsp].tranc[c];
if(s[lsq].len==s[lsp].len+1)
{
s[nwp].pre=lsq;
}else
{
int nwq=++siz;
s[nwq]=s[lsq];
s[nwq].endpos=0;
s[nwq].len=s[lsp].len+1;
s[lsq].pre=s[nwp].pre=nwq;
while(s[lsp].tranc[c]==lsq)
{
s[lsp].tranc[c]=nwq;
lsp=s[lsp].pre;
}
}
}
las=nwp;
}(考虑增量构造法的原理,后缀自动机在构造时显然应该一个一个插入)
这样的话后缀自动机的构造就结束了