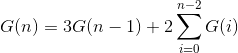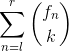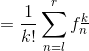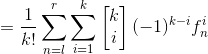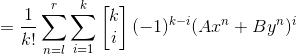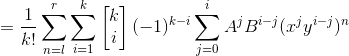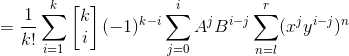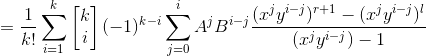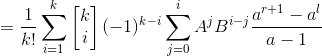【BJOI2019】勘破神机【数论】

传送门（难得正经一回）

神题，思想值得学习。

首先明确题意：

两个子问题，一个2xN,一个3xN。

接下来对这个问题进行慢慢的推敲

解方案数

很明显，我们要先解决放置方案数的公式，才能做这个题。

对于2xN

根据GXOI/GZOI2019逼死强迫症的博客推导我们易知

也就是斐波那契。

对于3xN

首先，n为奇数的时候，无方案，因为会有1个多余格子。

接下来，我们的n都表示原方案的2*n。

首先根据样例，3*2有三种方法。

所以肯定有的贡献。

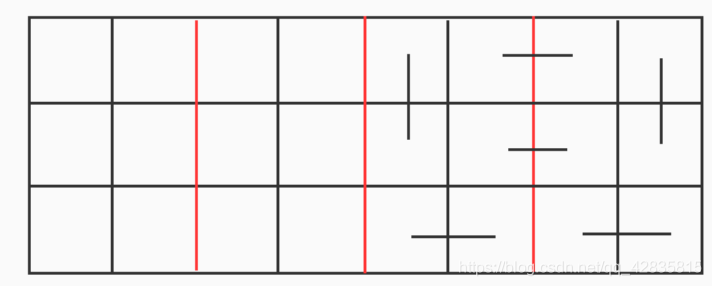
但这样是考虑不完整的。因为如果我和上一列结合，还会有方案。图长这样

 

 

继续根据广西广州OI那道题的单个格子分析我们可以发现，如果我们横跨到了上一个3*2，那放法也是唯一确定的。

所以最后我们得到

这个sigma太恶心，我们使用差分法得到进一步结论。

下式减上式得

所以

 

现在我们得到了F和G的表达式。但因为l和r太大，我们应该转成通项公式表达更优秀。

使用特征方程。

接下来都是我自己瞎想的，不保证正确性

我假设F是一个等比数列，设

根据递推式得

将F(n-2)视作常量，解得

根据zxyoi说的哈密顿-凯莱定理（看不懂）我们可以断定通项公式肯定是由这两个解的n次方构成的。

所以我们设

随便带两个值进去就解出来了。得到

同样解G得到

将根号部分视为虚部，重载几个运算符。

式子推导

刚刚解决了后面的方案数问题。而原式子后面是从这些方案里选k个的方案数。

我们发现用特征方程解出来的F和G都可以表示成。下面统一这么表示。

不论问的是F或者G，我们设其为f。将组合数表示成下降幂用第一类斯特林转成幂次方。

对于后面进行二项式展开，发现跟n有关的只有最后一块。所以等比数列表示出来。

所以询问就是

令，让式子好看点

现在式子的复杂度只和k有关了。而k小于501。那么直接算就是了。

我被坑了的地方

除了变量名重复爆炸之外，，我犯得最大错误就是

k小于501不是500。

然而很多数据是卡满501的。

所以预处理很多东西全都死掉了。

#include
using namespace std;
#define in read()
#define int long long
int in{
	int cnt=0,f=1;char ch=0;
	while(!isdigit(ch)){
		ch=getchar();if(ch=='-')f=-1;
	}
	while(isdigit(ch)){
		cnt=cnt*10+ch-48;
		ch=getchar();
	}return cnt*f;
}
const int mod=998244353;
struct gugu{
	
	int x,y;
	gugu(int xx=0,int yy=0){
		x=xx;y=yy;
	}
};
int V;
gugu operator +(gugu a,gugu b){
	return gugu((a.x+b.x)%mod,(a.y+b.y)%mod);
}
gugu operator -(gugu a,gugu b){
	return gugu((a.x-b.x+mod)%mod,(a.y-b.y+mod)%mod);
}
gugu operator *(gugu a,gugu b){
	return gugu((a.x*b.x%mod+V*a.y*b.y%mod)%mod,(a.x*b.y%mod+a.y*b.x%mod)%mod);
}
gugu operator *(gugu a,int b){
	return gugu((a.x*b%mod),(a.y*b)%mod);
}
int c[503][503],s[503][503];
int fac[503],ifac[503],inv2,inv6,inv10;
int ksm(int a,int b){
	int sum=1;
	while(b){if(b&1)sum=sum*a%mod;a=a*a%mod;b>>=1;}
	return sum;
}
gugu ksm(gugu a,int b){
	gugu sum=gugu(1,0);
	while(b){if(b&1)sum=sum*a;a=a*a;b>>=1;}
	return sum;
}
gugu inv(gugu a){
	return gugu(a.x,mod-a.y)*ksm((a.x*a.x%mod-V*a.y*a.y%mod+mod)%mod,mod-2);
}
int t,n,l,r,k;
gugu A,B,a,b;
int len,ans;
signed main(){
	t=in;n=in;inv2=ksm(2,mod-2);inv10=ksm(10,mod-2);inv6=ksm(6,mod-2);if(n==2)V=5;else V=3;
	for(int i=0;i<=503;i++)c[i][0]=1;s[0][0]=1;
	for(int i=1;i<=503;i++){
		for(int j=1;j<=i;j++){
			c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
			s[i][j]=(s[i-1][j-1]+(i-1)*s[i-1][j]%mod)%mod;
		}
	}
	fac[0]=1;
	for(int i=1;i<=501;i++)fac[i]=fac[i-1]*i%mod;
	ifac[501]=ksm(fac[501],mod-2);
	for(int i=500;i>=1;i--)ifac[i]=ifac[i+1]*(i+1)%mod;
	ifac[0]=1;
	//for(int i=0;i<=100;i++)cout<>=1;l=l+1>>1;
		}len=r-l+1;
		for(int i=1;i<=k;i++){
			gugu tm(0,0);
			for(int j=0;j<=i;j++){
				gugu AA=ksm(A,j);
				gugu BB=ksm(B,i-j);
				gugu YY=ksm(a,j)*ksm(b,i-j);
				gugu ri=(ksm(YY,len+1)-YY)*inv(gugu((YY.x+mod-1)%mod,YY.y));
				if(YY.x==1&&YY.y==0)ri=YY*(len%mod);
				//cout<<<