算法(1)——递归
什么是递归,我送理解的递归就是一直往前传递,直到尽头,返回归还一个结果到开始处就是递归;
递归是一种应用非常广泛的算法(或者编程技巧)。很多数据结构和算法的编码实现都要用到递归,比如DFS深度优先搜索、前中后序二叉树遍历等等
1.举实际中的例子
一排士兵排成一队,中间某一个士兵想知道自己在第几位,如何知道呢,他可以问他前一个人在第几个位置,前一个人也往前问,一直到第一个人,这个过程即为递,第一个人,告诉第二个人,再一直往后传,到中间士兵的位置,即为归。
f(n)=f(n-1)+1 其中,f(n)表示自己所在的位置,f(n-1)表示前一个人所在的位置,当f(1)=1时结束递,开始归。
int f(int n) {
if (n == 1) return 1;
return f(n-1) + 1;
}
这是一个最简单的例子,其中我们可以总结一下三个条件,只要同时满足以下三个条件,就可以用递归来解决。
1.一个问题的解可以分解为几个子问题的解何为子问题?子问题就是数据规模更小的问题。比如,前面的例子,你要知道,“自己在哪”的问题,可以分解为“前一个的人在哪”这样一个子问题。
2.这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样。
3.存在递归终止条件把问题分解为子问题,把子问题再分解为子子问题,一层一层分解下去,不能存在无限循环,这就需要有终止条件。第一排的人不需要再继续询问任何人,就知道自己在哪一排,也就是f(1)=1,这就是递归的终止条件。
再来一个复杂一点的例子
假如这里有n个台阶,每次你可以跨1个台阶或者2个台阶,请问走这n个台阶有多少种走法?如果有7个台阶,你可以2,2,2,1这样子上去,也可以1,2,1,1,2这样子上去,总之走法有很多,那如何用编程求得总共有多少种走法呢?
首先用上边的方法拆分一下问题每次你走的时候只有两个选择:走一步,或者走两步,没错吧,走了一步的话接下来就是n-1个台阶的走法,f(n-1)走了两步的话接下来就是n-2个台阶的走法,f(n-2),拆分出来就是fn=f(n-1)+f(n-2)
这个就是子问题确定了,接下来就是要找出终止条件。
什么情况下会终止呢?
我们想一下走到最后会是什么情况
(1)、剩一个台阶,只有一种走法,走一步,递归结束;
(2)、剩两个台阶,两种走法,走两次一步,或者走一次两步,递归结束;
(3)、剩三个台阶,一次两步,一次一步都结束不了(终止条件不成立)
所以剩一个或两个台阶时为终止条件。
public class Recursive {
public static void main(String[] args){
System.out.println(Recursive.number(5));
}
public static int number(int num){
if(num == 2){
return 2;
}
if (num == 1 ){
return 1;
}
return number(num - 1) + (num - 2);
}
}
递归这么好用,又存在哪些限制呢?
递归代码要警惕堆栈溢出
在实际的软件开发中,编写递归代码时,我们会遇到很多问题,比如堆栈溢出。而堆栈溢出会造成系统性崩溃,后果会非常严重。为什么递归代码容易造成堆栈溢出呢?我们又该如何预防堆栈溢出呢?
函数调用会使用栈来保存临时变量。每调用一个函数,都会将临时变量封装为栈帧压入内存栈,等函数执行完成返回时,才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大,调用层次很深,一直压入栈,就会有堆栈溢出的风险。
那么,如何避免出现堆栈溢出呢?
我们可以通过在代码中限制递归调用的最大深度的方式来解决这个问题。递归调用超过一定深度(比如1000)之后,我们就不继续往下再递归了,直接返回报错。
还需要警惕重复计算
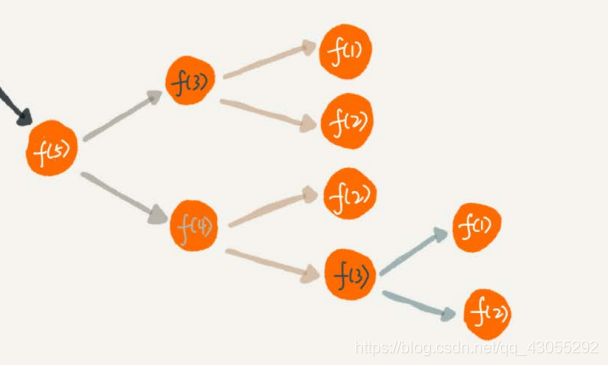
像上边走台阶的问题f(3)就被计算了好几遍,可以将结果存在一张散列表中,用n做key,调到f(n)时将值取出来直接用。
实际应用
权限关系中找到父级
long findRootReferrerId(long actorId) {
Long referrerId = select referrer_id from [table] where actor_id = actorId;
if (referrerId == null) return actorId;
return findRootReferrerId(referrerId);
}