我没喝醉,只是道路太坎坷。太曲折。 — 每天翻译一篇教程,这就是我写给houdini的情书。 【首发于同名公众号:“致houdini的情书”】 <Entagma>Houdini 2016
█ 我才不要过那种一帆风顺的人生呢!太乏味!
小马过河:
从前,有匹小马要过河。
老水牛看到了,对他说:“别怕,水很浅,只到了我的膝盖。”
小松鼠立刻跑了过来喊道:“不要相信他,水很深,我的朋友就是在这里淹死的!” 小马不知道该听谁的。
马妈妈在旁边说道:“孩子!别理那两个神经病了,咱们走桥!”
下面是一个粒子的自我修养:
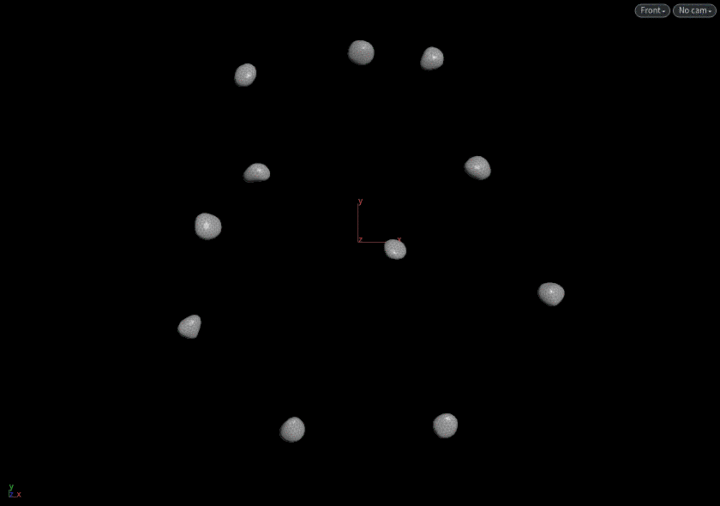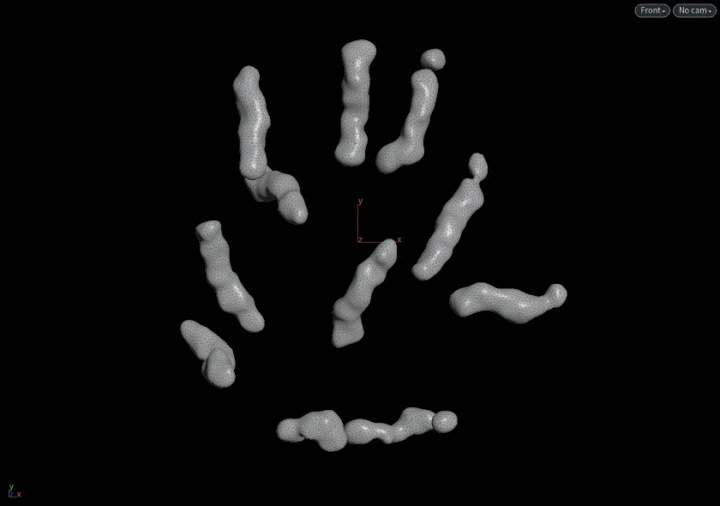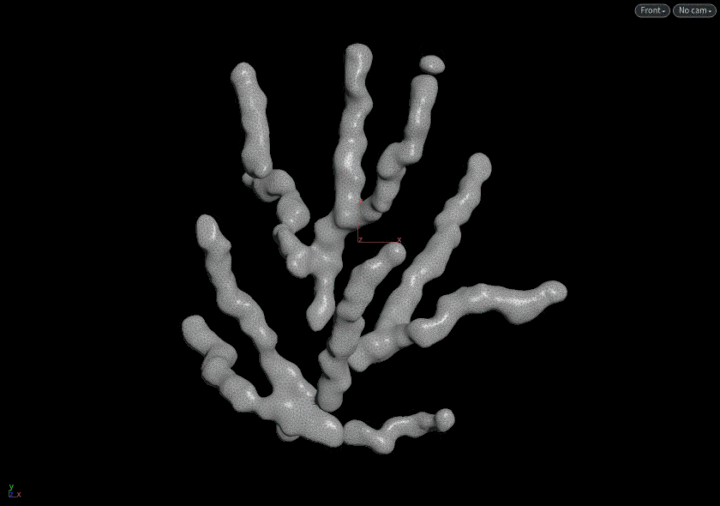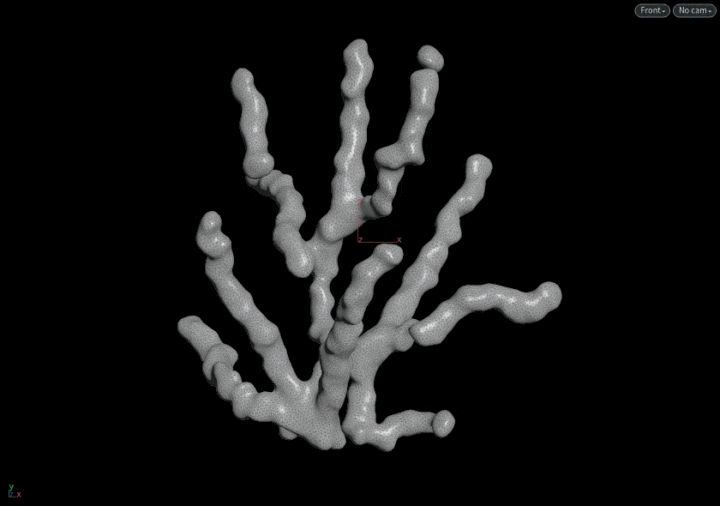
它要如何绕过前面的层层阻碍,到达它的梦想之地?
这一节要实现的效果.....
▉今天是42岁第003天周日
这是写给houdini的
第029封“情书”
我是geo流程图
我是solver流程图
本节需要注意的知识点:
1
实现从start绕过障碍物到达end的思路
1)首先在空间中填满点。
2)然后求得start和end之间全局方向适量。
3)再在寻找start的临近点。
4)求得start与临近点的局部方向矢量。
5)求得两个方向矢量的夹角.
6)取得最小的那个夹角.
7)取得最小夹角对应的点id。
8)当前点和最小夹角点各自移入相应的组里。
2
如何让start点在充满点的路径空间里始终保持id=0,
1)首先start连接active组,设置在这个组里。
2)然后路径空间的点连接active组,设置不在这个组里,但是有这个active组属性。
3)最后用merge合并。
3
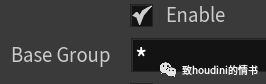
group与老版本区别
1)老版本Base Group:
a) * : “星号”表示选择所有点。
b) !* :"叹号+星号"表示全部不选
2)老版本Base Group:
a) 什么都不输入:表示选择所有点。
b) * : "星号"表示全部不选
4
本节使用函数的作用
1)point函数:通过找到end的位置,得到全局方向矢量
vectortgt = v@P - point(1,“P”,0);
2)inpointgroup函数:通过判断@ptnum当前点在active组里来确定执行“寻找它的临近点”。
if(inpointgroup(0,"active",@ptnum)){
3)pgfind函数:在!active组里找@ptnum的临近点列表closepts。
intclosepts[] =pgfind(0,“!active”,v@P,searchrad,maxpts,searchrad);
4)foreach函数:遍历临近点列表closepts的所有点cpt,来找出那个最小角度的点nextpt。
foreach(int cpt; closepts){
5)dot函数:在数学中,数量积(dot product; scalar product,也称为点积)是接受在实数R上的两个向量并返回一个实数值标量的二元运算。
dot(normalize(tgt),normalize(cptgt))
6)acos函数:返回参数的反余弦。求得角度数值。
floatangle =acos(dot(normalize(tgt),normalize(cptgt)));
7)setpointgroup函数:设置点移入移出相应的组。
setpointgroup(0,“active”,nextpt,1);
setpointgroup(0,“active”,@ptnum,0);
setpointgroup(0,“path”,@ptnum,1);
接下来
理论部分
问题1:如何实现绕过障碍从start到end的路径
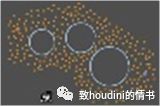
01)假使我们希望从A到B
02)但是路径上充满障碍
03)如何找到绕经路线
04)可以用点填满障碍的周围 :
05)当然首先要画一条到B的矢量:
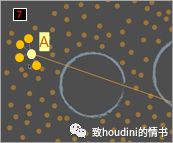
06)第二步找到距离A一定范围的点:
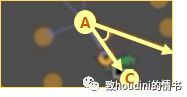
07)从中选择距离这条line最近的点:
08)根据测量点到line的角度来判断:
08)C就是我们的下一个点
接下来
开始正式制作
使用软件houdini16.0.633
问题1:路径绕过障碍的空间如何填满点
1 创建隔离障碍物
1)sphere1
a) frequency=32
2)sphere2: 复制<1>
3)isooffset1
a) Fog volume
4)Scatter1
a) Count=50 ;//分布50点作为障碍物
b) 关闭松弛;
5)pointwrangle1
a) 创建pscale属性 ; //建立点的随机大小
f@pscale = fit(rand(@ptnum + chi(“seed”)),0,1,0.05,0.3)
大小随机
6)Relax1
a) Iter=200
b) √ relax in 3D //使球体错落分离
分离
1)sphere 1
a) uniform scale :0.85
7)copytopoint
8)vdbfrompoly1
a) Voxel:0.02
2 创建障碍物与外面大圆vdb布尔运算得到绕过障碍的路径VDB空间
9)sphere3
a) scale=1.8
b) frequency=32
10)vdbfrompoly2 复制<8>
11)vdbcombine
a) Operation:SDF Difference
b) 槽1接<10> ;槽2接<8>
12)volumeslice 切片
a) 改变offset检查相交
vdb
13) convervdb 转成fog
1) VDB
2) SDF to Fog
转成fog粒子经过路径的空间
3 障碍物外面空间填满点
14) scatter2:
1) Iter=4
2) Count=10万 //增加点的密度
//创建start和end两个点
4 增加起点start&终点end
15)add 1: //命名 add_start
1) Y=1.7
start点
16)add 2: //命名 add_end
1) Y=-1
5 建立active组,确保start点id=0
分析)
group1:搜索的出发点的周围点(用于测量角度)放入这个组。
group2:这条路径上的点放到这个组。
//创建两个group
17)group1:
a) name:active
b) Entity:points
c) 连接<15>
start点在:active组里
18)group2:
a) 复制<17>
b) 不含任何点: * //不归入active
c) 连接<14>
填充的点有active属性,但不在active组里
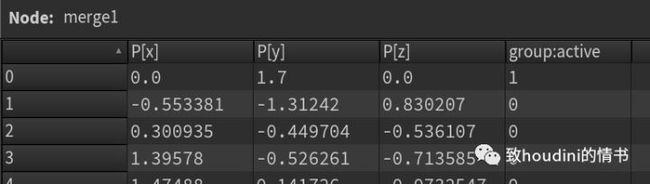
19)merge1
a) 合并两个group
现在我们已经为后面的pointwrangle里点移入active组做好准备。
20)pointwrangle2
第1步:新建从start到end点的“全局方向 ” tgt
end连接槽1,它的id=0
vectortgt = v@P -point(1,“P”,0);
第2步:判断如果当前点在active组里返回1;执行内部代码
if(inpointgroup(0,"active",@ptnum)){
第3步:求当前点四周的“临近点”closepts,而且要在“!active”(非active)组里寻找;
intclosepts[] =pgfind(0,“!active”,v@P,searchrad,maxpts,searchrad);
第4步:foreach循环遍历点列表里每个临近点cpt
foreach(int cpt; closepts){
第5步:求当前点(start)与临近点的“局部方向”cptgt
vectorcptgt = v@P -point(0,“P”,cpt);
第6步:用“三角函数” 求夹角angle(两个方向"tgt"和"cptgt"的)
floatangle =acos(dot(normalize(tgt),normalize(cptgt)));
第7步:找到最小的angle
floatoangle = 1000;
if(angle oangle = angle; 第8步:更小的angle对应的id //-----初始化变量 int nextpt = -1; nextpt = cpt; 第9步:把所有点各自归入相应的组 setpointgroup(0,“active”,nextpt,1); nextpt就是下一个点添加进active, setpointgroup(0,“active”,@ptnum,0); //@ptnum(当前点id)移出active组 21)solver1 a) pointwrangle2拷入, b) 连接 22)delete1 a) Group:active; b) Operation: Delete on-select c) Entity:points 现在只显示一个点,因为vex每次只产生一个点, /第10步: 1)在外面建一个path组 23)group3 a) Group:path; b) Base Group: * 2)把当前点归入path组 setpointgroup(0,“path”,@ptnum,1); //@ptnum移入path组里 22)delete1 a) Group:path ;//改成保留path组的点 剩下的可以:可以把start换成多个点 =vex代码!== //---------------- <区域1>找到start周围指定半径范围内的点------------------ //----- “搜索半径”,“最大点数”两个变量---- float searchrad = 1.0; int maxpts = 32; //-----旧的角度变量old angle 设一个很高的值---- float oangle = 1000; //-----初始化变量 int nextpt = -1; //-------第1步:新建从start到end点的“全局方向 ” tgt--------- vector tgt = v@P - point(1,“P”,0); //当前点位置-“槽1”的点的位置,ptnum=0 //-------第2步:判断如果当前点(start)在active组里返回1;执行内部代码-------------- if(inpointgroup(0,"active",@ptnum)){ //--------第3步:求当前点(start)四周的“临近点”closepts (!active组里)-------- int closepts[] = pgfind(0,“!active”,v@P,searchrad,maxpts,searchrad); //在 “!active”组,搜索半径=searchrad,增加两个新增变量maxpts,searchrad,第二个searchrad是搜索精度divsize,大多数情况divsize跟radius相同, //------------------ <区域2>测量角度,找出最小角度的点------------------- //--------第4步: foreach循环遍历点列表里每个临近点cpt------------- foreach(int cpt; closepts){ //新变量countpoint=cpt //--------第5步:求当前点(start)与临近点的“局部方向”cptgt ---------- vector cptgt = v@P - point(0,“P”,cpt); //从当前点start到cpt(count point target)点 //--------第6步:用“三角函数” 求夹角angle(两个方向"tgt"和"cptgt"的)--------- float angle = acos(dot(normalize(tgt),normalize(cptgt))); // dot返回点积:两个向量并返回一个实数值标量 //--------第7步:找到最小的angle---------- //使用if语句,检查curent angle---分析:如果angle<前一个angle,它就被写进oangle-- if(angle oangle = angle; //-------第8步:更小的angle对应的id--------; , nextpt = cpt; } } //. -------第9步:把nextpt和当前点各自归入相应的组--------- setpointgroup(0,“active”,nextpt,1); nextpt就是下一个点添加进active, setpointgroup(0,“active”,@ptnum,0); //@ptnum(当前点id)移出active组 //. -------第10步:把当前点归入path组,在外面建一个path组-------- setpointgroup(0,“path”,@ptnum,1); //@ptnum移入path组里 } 今天就到这儿了,收功 教程翻译自entagma的网络教程 下一节:20170102 Special Guest - Ben Watts- Shortest Path Growth最短路径增长 本文图片全部原创,版权归原作者所有。