DDA、Bresenham直线画线算法,中点圆、中点椭圆算法&可视化(Python3实现)
本文主要技术:直线、圆、椭圆四种绘制算法,Python3(Matplotlib,PyQt5)
本文是笔者上计算机图形学课程时课内实验的报告,内容仅供参考。
1-实验目的及要求
- 实现直线、圆、椭圆的四种绘图算法,保证其在所有可能情况下给出正确结果;
- 封装计算程序,并设计图形界面,实现接收绘图参数输入和展示绘制实际图像的图形化绘图程序。
2-实验环境
本实验在Ubuntu16.04下完成,编程语言为Python3. 在此基础上,调用的非默认包包括Matplotlib和PyQt5,其中绘图选项和图像展示使用Matplotlib实现,而接受输入参数的输入框使用PyQt5实现。
在终端中输入如下指令,以配置上文所述的实验环境:
sudo apt-get install python3
sudo apt-get install python3-pip
pip3 install matplotlib
sudo apt-get install python3-pyqt5
执行上述指令即可完成环境配置。
3-实验内容和程序实现
绘图程序的项目结构(调用关系)如下图所示:
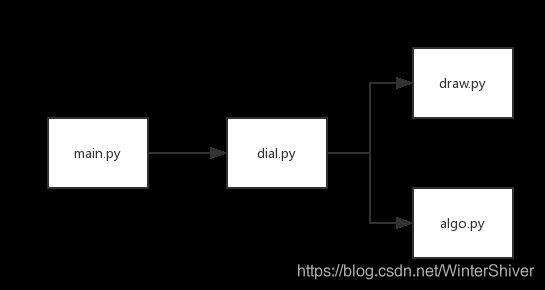
图3-1 整体项目结构
实验中使用的参数、常数和类型标记原本用单独的文件维护,但考虑到Python中常量不能直接跨文件传递(只能通过调用传递,低效且不便),所以后期放弃了这个设计,而是在每个文件中都重新定义常量。
main.py:主程序
main.py中定义了默认绘图窗口的排布,并定义了按下按键时的发生的事件。
if __name__=="__main__":
# Initialize
fig = plt.figure()
# Multiple Button
rax = plt.axes([0.65, 0.8, 0.25, 0.15])
# Draw
ax = plt.axes([0.15, 0.15, 0.6, 0.6])
fig.add_axes(ax)
drawAxis()
plt.show()
上述代码分别定义了按键框和坐标轴的位置和大小,并对其进行描绘,显现初始界面的布局。绘图界面的初始状态如下图所示:

图3-2 绘图初始界面
初始界面的窗口大小、坐标轴范围均可调整。
图示的按钮由matplotlib.widgets中的RadioButtons,即单选框来实现:
algoList = ("DDA", "Bresenham",
"Mid-Point Circle", "Mid-Point Ellipse")
radio = RadioButtons(rax, algoList)
radio.on_clicked(pressEvent)
def pressEvent(label):
app = QApplication(sys.argv)
if label == "DDA":
myshow = InputDialogDDA()
elif label == "Bresenham":
myshow = InputDialogBresenham()
...
myshow.show()
sys.exit(app.exec_())
pressEvent函数将选择框的四个按钮和四种算法的参数输入框相绑定,实现点击按钮输入参数的功能, 而保存参数和调用绘制函数的功能则由下文所述的参数框实现。
dial.py:参数输入框的定义
dial.py中定义的对象是四种算法参数接受框的实现,本质上是可以接收输入文本的窗口,通过PyQt5构建。以Bresenham算法的参数接收框为例,其中主要包括如下要素:
- 文本框,作用是显示提示文本。
labelBeginX = QLabel("Begin Point, X:")
- 下沉文本框,在显示提示文本的同时可以修改文本的值,因为文本框是窗口对象的一个成员变量,它显示的文本储存在窗口类中,是可以修改的。同时,对文本框施加下沉效果,提升观感。
self.bxLabel = QLabel("0")
self.bxLabel.setFrameStyle(QFrame.Panel|QFrame.Sunken)
- 按钮,在按下时执行对应的函数。此处执行的函数实现对话框弹出的效果,从对话框接受输入并修改属性值。
bxButton=QPushButton("Set X")
bxButton.clicked.connect(self.selectBxNumber)
def selectBxNumber(self):
number,ok = QInputDialog.getInt(
self,
"Input a Number",
"Please Input a Number:",
int(self.bxLabel.text()),
min = -CONST_INFTY,
max = CONST_INFTY,
step = 1)
if ok :
self.bxLabel.setText(str(number))
最后,绘制输入框界面,并合理排布文本框
最后,输入框通过按钮对接绘图函数,根据输入的参数绘制图形。
drawButton=QPushButton("Draw Now!")
drawButton.clicked.connect(self.drawNow)
def drawNow(self):
x1 = int(self.bxLabel.text())
y1 = int(self.byLabel.text())
x2 = int(self.exLabel.text())
y2 = int(self.eyLabel.text())
color = self.colorLabel.text()
pointList = Bresenham(x1, y1, x2, y2)
draw(TYPE_LINE, pointList, 0, 0, color)
draw.py:绘图函数的定义
draw.py定义了draw()函数及其子函数,用于在图形界面上画图。绘图技术由Matplotlib提供,以下简称为plt. 具体而言,draw()函数接收绘图点列,并根据指定的绘图对称方式在界面上逐点绘制图像。
draw()函数在plt的交互模式开启时绘图,首先调用drawAxis()绘制坐标轴,再根据对称方式调用
def draw(type, pointList, centerX, centerY, pointColor = "blue"):
# Axis Initialization
plt.ion()
drawAxis()
# Decide Type
if type == TYPE_LINE:
draw1(pointList, pointColor)
elif type == TYPE_CIRCLE:
draw8(pointList, centerX, centerY, pointColor)
elif type == TYPE_ELLIPSE:
draw4(pointList, centerX, centerY, pointColor)
plt.ioff()
plt.draw()
举无对称的情况为例,draw1()函数展现了逐点绘图的过程:在交互模式开启的情况下,从点列逐个取出点,用函数plt.scatter()绘制,并添加一定的时间间隔,以体现逐点绘制过程。
def draw1(pointList, pointColor):
for i in range(len(pointList)):
[x, y] = pointList[i]
plt.scatter(x, y, color = pointColor)
plt.pause(para.pauseTime())
algo.py:绘图算法实现
algo.py提供底层的算法实现。四种绘图算法用函数封装,接收绘图参数并以list类型返回待绘制的点列。在下面的部分详细说明。
4-数据结构和算法描述
对于DDA和Bresenham算法,以绘制斜率 m ∈ ( 0 , 1 ) m\in(0,1) m∈(0,1)的情况为例,算法的本质是将整数横坐标上的每一个点的纵坐标四舍五入确定为整数。Bresenham算法实际上优化了这个过程,避免执行 O ( n ) O(n) O(n)次的大浮点数计算和取整,而是将整数和小数分开储存:算法中计算的决策参数p实际对应当前绘制的整数坐标舍入时超出或不足的部分,所以可以根据p的正负对舍入进行判断。对于斜率为其他或绘制方向不同的情况,可以通过轴对称、中心对称和坐标对称来生成对应的点列。
中点圆算法中继承了上述的三处比较重要的思想:一是利用中间点的判断确定绘图点的整数坐标。中点圆算法依然判断半整数点所处的位置来确定绘制哪个点更合理,并把这个特性提炼成为绘制的决策参数。二是利用迭代代替重复计算。类似直线画线算法,中点圆算法中也为每次更新决策参数设计了复杂的机制,以尽量使用整数计算和整数判断,减少计算量。三是充分利用对称性。由圆的八对称性质,中点圆算法只需要计算角坐标 θ ∈ [ π 4 , π 2 ] \theta\in[\frac{\pi}{4},\frac{\pi}{2}] θ∈[4π,2π]的部分,而其他部分直接对称绘制。类似地,因为椭圆的性质弱化到四对称,所以中点椭圆算法分别绘制角坐标为 θ ∈ [ π 4 , π 2 ] \theta\in[\frac{\pi}{4},\frac{\pi}{2}] θ∈[4π,2π]和 θ ∈ [ 0 , π 4 ] \theta\in[0,\frac{\pi}{4}] θ∈[0,4π]的两个部分,再对称到其他位置。
以下以Bresenham算法为例结合程序说明。
def Bresenham(x1, y1, x2, y2):
pointList = []
if x1 == x2: # Special Case: Horizenal Line
if y1 <= y2:
return [[x1, y] for y in range(y1, y2 + 1)]
else:
pointList = [[x1, y] for y in range(y2, y1 + 1)]
pointList.reverse()
return pointList
elif abs(y2 - y1) <= abs(x2 - x1): # abs(slope) <= 1
return _Bresenham(x1, y1, x2, y2)
else: # abs(slope) >= 1: Axis Reverse
pointList = _Bresenham(y1, x1, y2, x2)
return [[p[1], p[0]] for p in pointList]
首先对直线绘制初步划定三种情况:当直线与y轴平行时直接绘制;当直线斜率的绝对值大于1时调换x,y轴,使方向变换后斜率小于1;在斜率的绝对值小于1时才真正用_Bresenham函数处理。
def _Bresenham(x1, y1, x2, y2): # abs(slope) <= 1
# Parameter of Drawing
slope = (y2 - y1) / (x2 - x1)
# Initialize
p = 2 * slope - 1
[x, y] = [x1, y1]
pointList = []
if x1 < x2:
if slope >= 0:
# Real Bresenham Algorithm
while True:
pointList.append([x, y])
if x == x2:
return pointList
if p <= 0:
[x, y, p] = [x + 1, y, p + 2 * slope]
else:
[x, y, p] = [x + 1, y + 1, p + 2 * slope - 2]
else: # Up-Down Symmetry
pointList = _Bresenham(x1, -y1, x2, -y2)
return [[p[0], -p[1]] for p in pointList]
else:# Left-Right Symmetry
pointList = _Bresenham(x2, y2, x1, y1)
pointList.reverse()
return pointList
在斜率的绝对值小于1时,利用x轴、y轴的轴对称(Up-Down Symmetry和Left-Right Symmetry)把绘制局限在斜率 m ∈ ( 0 , 1 ] m\in(0,1] m∈(0,1],从左到右绘制的情况。在此情况下,要对于每一个x坐标计算一个y坐标,而且每次确定y时y要么不变,要么增加1。
Bresenham算法通过维护一个决策参数p来确定y是否增加,p实际对应整数坐标舍入时超出或不足的部分:记 y k = m x k + b y_k=mx_k+b yk=mxk+b为实际的直线纵坐标, y ^ \hat{y} y^为舍入后的整数坐标,则有 p k = 2 y k + 1 − 2 y ^ k + 1 + 1 p_k=2y_{k+1}-2\hat{y}_{k+1}+1 pk=2yk+1−2y^k+1+1
在此情况下,只需要每次通过预判更新p,再由p指导y是否增加即可。这就是算法的主要思想。具体而言,p的更新由以下伪代码说明:
- p 0 = 2 m − 1 p_0=2m-1 p0=2m−1, x 0 = x 1 x_0=x_1 x0=x1
- while x k < x 2 x_k
xk<x2
if p k ≤ 0 p_k\leq0 pk≤0: y k + 1 = y k y_{k+1}=y_k yk+1=yk, p k + 1 = p k + 2 m p_{k+1}=p_k+2m pk+1=pk+2m
else: y k + 1 = y k + 1 y_{k+1}=y_k+1 yk+1=yk+1, p k + 1 = p k + 2 m − 2 p_{k+1}=p_k+2m-2 pk+1=pk+2m−2- x k + 1 = x k + 1 x_{k+1}=x_k+1 xk+1=xk+1
计算过程中的点列即为需要绘制的点列,将其记录返回即可。
5-调试过程和实验结果
运行主程序:
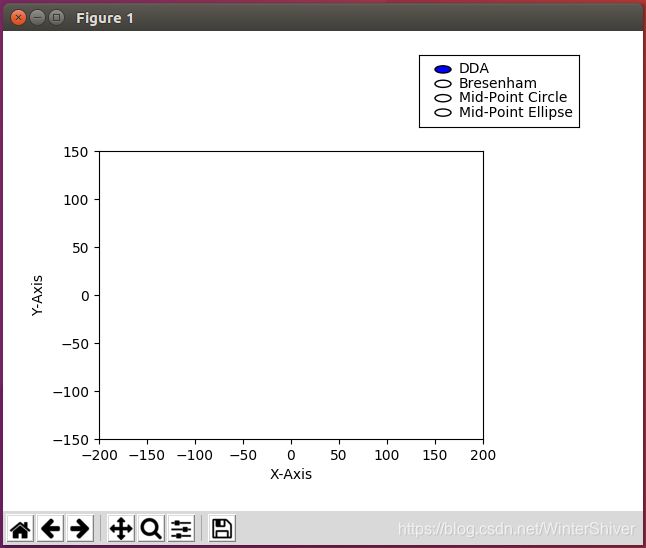
图5-1 绘图程序的主界面
主程序构造了绘图的初始图形界面,其中坐标轴已经绘制,并给出了绘图选项,等待接收输入。
通过鼠标单击绘图选项输入绘图参数:单击之后,将弹出形如图5-2的绘图窗口来接收输入。
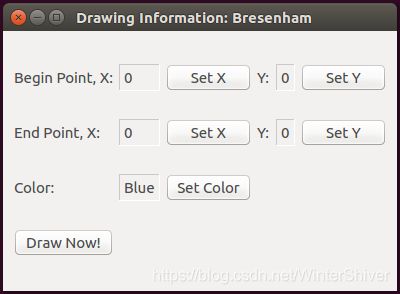
图5-2 接收绘图参数
接收绘图参数后,程序逐点绘制指定图形,并在界面上显现。效果如下所示:
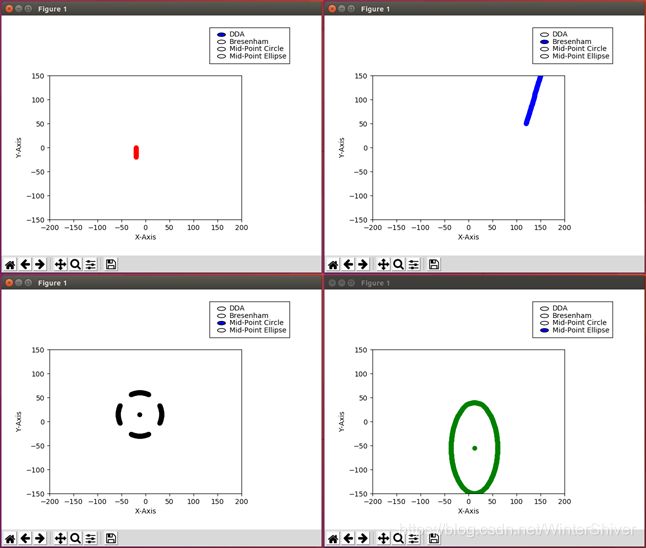
图5-3 直线、圆、椭圆的绘制结果