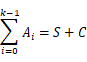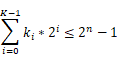如何在FPGA中实现高效的compressor加法树
引言
大规模的整数加法在数字信号处理和图像视频处理领域应用很多,其对资源消耗很多,如何能依据FPGA物理结构特点来有效降低加法树的资源和改善其时序特征是非常有意义的。本篇论文是基于altera公司的FPGA,利用其LUT特点,探索设计最大程度利用LUT以及改善时序的compressor树的结构。
1 半加器和全加器
半加器是两个输入bit相加,输出结果S和进位C。表达式为:
S=A^B![]()
C=A∙B![]()
全加器是三个bit相加,有进位参与,表达式为:
Si=Ai^Bi^Ci-1![]()
Ci=Ai∙Bi+Ai+Bi∙Ci-1![]()
Compressor树就是在全加器的基础上建立的,通过全加器的S和C结果相互连接形成多层树状结构,其相比于普通的进位加法树消耗更少资源。普通进位加法树是用两个或者三个加法模块连接成树,形成多层结构来计算多输入加法。放一张wallace树的经典文献中的图片来大致了解一下compressor树的结构。
图1.1 compressor树结构
2 Compressor树
Compressor树就是在图1.1中carry propagating adder以上的部分,其目的就是为了减少被加数个数,上图中降低到S和C两个后送到进位链加法器完成最后求和。这样就可以降低加法对资源的消耗。假设有如下加数:
Ak-1, Ak-2, …, A0![]()
Compressor树的结果就是:
Compressor树就是由以上的全加器构成的。全加器构成一个基本的并行计数器,并行计数器(Generalized parallel counters)GPC可以用一个元组表示:
KK-1, KK-2, …, K0;n![]()
其中Ki表示的是输入的被加数中处于同一位置的bit个数,如果用点来代表bit,那么下图中的bit0的个数有1,而bit1有2,bit2有3,…。假设一个GPC允许的最大输入bit数为M,这个条件是考虑到FPGA中LUT的结构,比如在altera的stratix等器件中,LUT是6输入的,为了更好的利用LUT资源,需要适配LUT输入。那么根据这个条件,可以得到以下的约束:
图2.1 (1, 4, 1, 5; 5)
第一个约束条件是所有列的bit数被限制在M以内,第二个条件是所能实现的最大数据范围。后边会根据这两个条件提出一个在FPGA上优化compressor树的算法。
用GPC来实现元组(1, 4, 1, 5; 5)为下图:
图2.2 实现元组(1, 4, 1, 5; 5)的GPC结构
从图中看出其延时包括一个FA的延时和4个进位链产生的延时。在FPGA中提供了高速的进位链,所以GPC很适合在FPGA中实现。因此在FPGA上利用好GPC可以降低加法树的级数。比如举个例子,如图2.3所示,计算两列数据和,如果使用华莱士树的方式,会采用两级电路,第一级用两个全加器,将三行数据降低到两行数据,最后再用一个进位链加法器实现最后数据相加。而如果使用GPC(3, 3; 4)仅仅用一级电路就能实现这三行数据的相加。
图2.3 compressor树构建方式:a)用连个全加器和进位链加法器 b)用一个(3, 3; 4)GPC
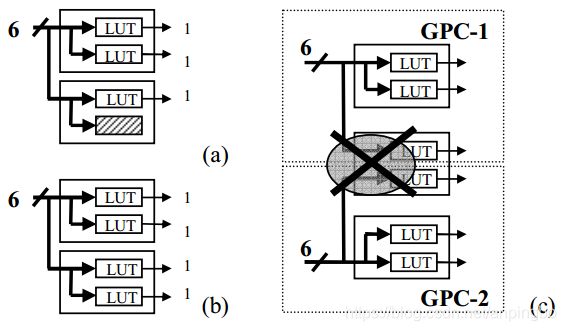
现在结合altera的器件结构来分析如何能更好的利用LUT来搭建一个GPC。Stratix器件中的adaptive logic module(ALM)包含两个6-LUT,这两个LUT共享输入,因此一个ALM模块可以实现6-2的功能。通过图2.4可以看出,如果将6输入3输出进行映射,会有一个LUT空置,利用率为75%。如果将6输入4输出映射到LUT,那么利用率为100%。如果将2个6输入3输出映射到2个ALM,这个无法实现,因为ALM中两个LUT共享输入则无法综合。
图2.4 (a)一个6-3GPC映射,只有75%利用率(b)6-4GPC映射,利用率100%(c)2个6-3映射到2个ALM不可实现
3 高效映射算法
为了提高LUT利用率,降低器件中逻辑使用面积,论文基于以上的两个约束以及altera LUT结构特点提出了GPC选择的算法。
首先我们定义两个概念,primitive GPC是满足以上约束的所有GPC集。比如对于M=6,n=3,一共有12个GPC。Covering GPC是指可以不被其它GPC实现的,即其实现是唯一的。比如(2, 2; 3)就不是一个covering GPC,因为其利用(2, 3; 3)GPC同样可以实现,只要将bit0对应的一个数置为0就行了。比如对于6-3GPC的covering GPC有{(0, 6; 3), (1, 5; 3), (2, 3; 3)}。而(3, 1; 3)是一个不够高效的GPC,因为其bit0只有一个bit有数,其可以绕过GPC直接输出。compressor ratio是输入对输出的比率,比如(2, 3; 3)的比率是5/3=1.66。
算法步骤如下:
- 首先依据M和n生成covering GPC;
- 产生一些列primitive GPC,compressor树将会由这些GPC来构建,但是最后将由对应的covering GPC来替代;
- 计算每个primitive GPC的compressor ratio并分类;
接下来的4-6步是一个不断迭代过程,每一次迭代生成一级GPC,直到达到k行和kbit每列的限制条件。
- 首先从所有求和列中选择一个bit数最多的列作为基准,然后再同时向前和向后进行搜索,比较前后两个列的compressor ratio,选择最大的作为将要用于GPC映射的列。不断重复这个过程直到所有列都完成搜索。
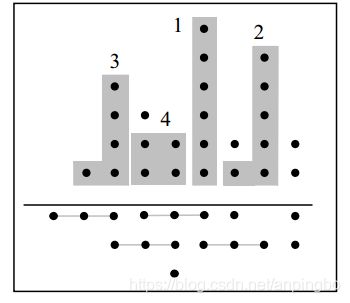
比如图3.1展示的是一个6-3GPC建立过程。
第一个GPC是有6个bit的列,可以用(0, 6; 3)GPC来表示;
第二个最高列是有5bit,可以用(1, 5; 3)表示,附带上旁边的一个bit;
第三个高列有4bit,可以用(1, 4; 3)GPC实现;
…。
这样共实现了4个GPC,余下的没有实现的bit使用GPC实现不能有效提高LUT利用率,直接传递到下一级。
图3.1 GPC生成过程
- 对步骤4生成的新bit重复步骤4,进行提取新的GPC;
- 当最终生成的bit行数小于k或者列数bit数小于k,迭代过程结束,这时上一级没有被分配GPC的bit传递到本级,通过一个进位链加法器将所有结果相加;
- 结果
论文比较了GPC和另外两种加法器实现方式的逻辑面积和资源对比,这另种加法器分别为:
1 ADD:由一个三输入加法器作为基本结构构建的加法树;
2 3GD:采用carry-save 加法器来实现,这种结构没有利用ALM中的进位链;
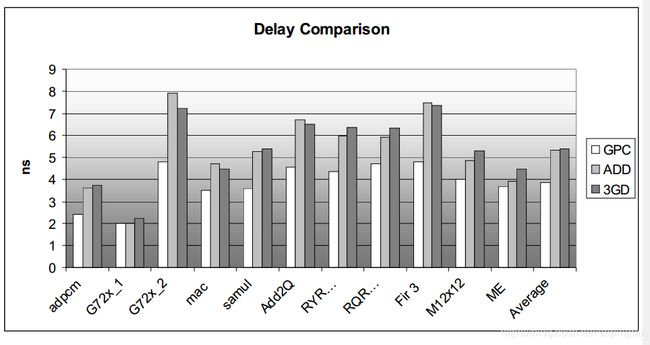
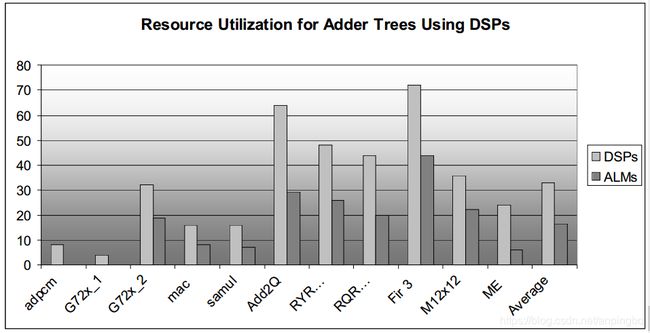
延时、逻辑面积、资源利用对比如下图所示:
图4.1 不同加法器实现方式的对比结果
总结
论文探索了利用FPGA的LUT和进位链结构来实现GPC,相比于ADD和3GD有更低的延时,而资源使用和ADD相差不大,比3GD小很多。这主要是源于ADD和GPC都使用了进位链。
[1]
- Hadi Parandeh-Afshar, P.B.a.P.I., Efficient Synthesis of Compressor Trees on FPGAs. IEEE Asia and South Pacific Design Automation Conference, 2008.