小波变换基础

小波变换基础

信号处理中的变换

在信号处理领域，存在很多变换，比如希尔伯特变换，短时傅里叶变换，Wigner 分布，Radon 变换和小波变换等。它们都实现了原始信号——时间信号的其他表示，即获得了信号在其他角度上（基上）的表示（系数）。比如最常用的傅里叶变换，其变换公式如下

根据欧拉公式：，可得

而由于任何周期函数都能使用不同的三角函数进行拟合，因此信号能够表示为

  

同时由于三角函数本身的正交性——不同频率的三角函数的乘积积分为零，因此对应  的变换结果就是对应频率上的信号强度。

傅里叶变换的重要地位也源于其实际的物理意义：变换结果为信号在对应频率上的强度。

其本质是信号在三角函数这族基（正交基）上的展开。而所有变换的本质都是度量测试信号与基信号的相似性，而对应基信号的参数就是对应变换的结果的参数。对应的级数展开就是对应变换结果与对应基信号的乘积的和。

小波基础

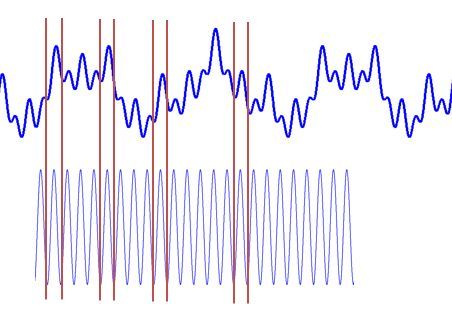
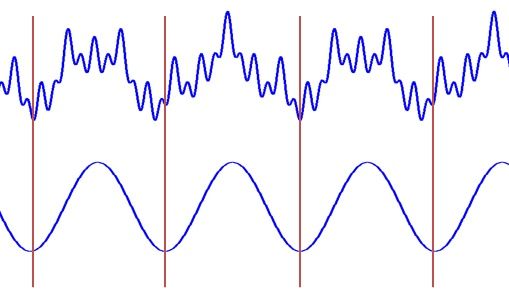
小波的原理理解和为什么要用小波可以参考：https://zhuanlan.zhihu.com/p/22450818 ，其中的一些图对于理解小波变换很有帮助。其中的基本内容概括起来就是以下几点：

1、傅里叶变换（ FT ）能够更好地分析信号的频率信息，但是由于 FT 必须对一段信号（持续一段时间）进行分析才能得到较准的频率结果，因此对于非平稳信号（信号的频率会不断变化），FT 只能得到这段时间内的频率分布，而并不能给出具体频率分量所在的时间。这就造成在时频上很不同的信号（频率上升和下降），FT 会得到相同的结果。

2、为改善 FT 对于时间的不敏感，提出了短时傅里叶变换 （ STFT ），即将这段信号加窗分成多段信号分别进行 FT 来对时间维分析结果进行改善。本质上，通过加窗 STFT 将大范围内的非平稳信号通过加窗分割为了多个小范围内的平稳信号，从而使得 FT 能够对非平稳信号进行有效地分析。但是其中涉及窗口大小的选择。如果窗口较大，时间分析的精度就会下降；而如果窗口较小，那么频率分析的精度就会下降。

3、其实频率和时间分辨率存在矛盾，理论上无法同时获得高的时间分辨率和高的频率分辨率（海森堡测不准原理）。因此小波变换通过多分辨率分析（Multi-Resolution Analysis, MRA）在高频部分给出好的时间分辨率，而在低频部分给出好的频率分辨率。这更加符合现实中高频信号通常持续时间较短，而低频信号持续时间较长的情况。实际中，小波变换将无限长的三角函数基换成了有限长的会衰减的小波基，并增加尺度（频率）和偏移（时间）维度，实现对信号时间和频率维的分析。

为进一步理解小波变换如何实现的多分辨率分析，必须了解尺度函数。这部分内容可以参阅（搜索）：小波变换和motion信号处理。

其中还推荐了几篇文章，这里也附在这里

1. THE WAVELET TUTORIAL
2. WAVELETS：SEEING THE FOREST AND THE TREES
3. A Really Friendly Guide to Wavelets
4. Conceptual wavelets

一维离散小波变换

这里以Haar小波为例：

原始采样信号：[6 4 8 7 5 9 3 2]

分解低通滤波器：[ 1  1]/sqrt(2)

分解高通滤波器：[-1 1]/sqrt(2)

变换过程：

1.用低通滤波器与原始像素矩阵做卷积得：[8 10 12 15 12 14 12 5]/sqrt(2)

下采样得：[10 15 14 5]/sqrt(2)    ----->    L

2.用高通滤波器与原始像素矩阵做卷积得：[-4 2 -4 1 2 -4 6 1]/sqrt(2)

下采样得：[2 1 -4 1]/sqrt(2)    ----->     H

逆变换过程：

重构低通滤波器：[1  1]/sqrt(2)

重构高通滤波器：[1 -1]/sqrt(2)

1.对L数组插值得：[0 10 0 15 0 14 0 5]/sqrt(2)

再用低通滤波器做卷积得：[10 10 15 15 14 14 5 5]/2

2.对H数组插值得：[0 2 0 1 0 -4 0 1]/sqrt(2)

再用高通滤波器做卷积得：[2 -2 1 -1 -4 4 1 -1]/2

两个数组求和得：[6 4 8 7 5 9 3 2] ，矩阵被还原了。

图像二维离散小波变换

其本质就是对行进行先进行一维离散小波变换，然后在对列进行一维小波变换，得到 LL 中包含图像的低频部分，HL 中包含水平方向的高频和垂直方向的低频（纵向的边界），LH 中包含水平方向的低频和垂直方向的高频（横向的边界），HH 中包含水平和垂直方向的高频（对角的边界）。

其具体实现方法（哈尔小波）可以简化为分别在水平和垂直方向取均值和做差来实现。

/*************************************************
Copyright:zhuchen
Author: zhuchen
Date:2016-01-10
Description:多级haar小波变换
**************************************************/


# include
# include

using namespace std;
using namespace cv;

int main() {
	Mat img = imread("lenna.bmp", 0);
	int Height = img.cols;
	int Width = img.rows;
	int depth = 3;    //定义分解深度
	int depthcount = 1;
	Mat tmp = Mat::ones(Width, Height, CV_32FC1);
	Mat wavelet = Mat::ones(Width, Height, CV_32FC1);
	Mat imgtmp = img.clone();
	imgtmp.convertTo(imgtmp, CV_32FC1);
	while (depthcount <= depth) {
		Width = img.rows / depthcount;
		Height = img.cols / depthcount;

		for (int i = 0; i < Width; i++) {
			for (int j = 0; j < Height / 2; j++) {
				tmp.at(i, j) = (imgtmp.at(i, 2 * j) + imgtmp.at(i, 2 * j + 1)) / 2;
				tmp.at(i, j + Height / 2) = (imgtmp.at(i, 2 * j) - imgtmp.at(i, 2 * j + 1)) / 2;
			}
		}
		for (int i = 0; i < Width / 2; i++) {
			for (int j = 0; j < Height; j++) {
				wavelet.at(i, j) = (tmp.at(2 * i, j) + tmp.at(2 * i + 1, j)) / 2;
				wavelet.at(i + Width / 2, j) = (tmp.at(2 * i, j) - tmp.at(2 * i + 1, j)) / 2;
			}
		}
		imgtmp = wavelet;
		depthcount++;
	}

	namedWindow("jpg", 0);
	wavelet.convertTo(wavelet, CV_8UC1);
	wavelet += 50;            //图像暗度过低，所以这里我加了50
	imshow("jpg", wavelet);
	waitKey(0);
	return 0;
}