影响我国GDP增长的主要因素（数据分析方法与R软件）

一、问题的提出

经济增长是我国宏观经济政策的目标之一，研究影响经济增长的因素对促进我国经济快速发展有着十分重要的意义。本次实验运用R软件编写代码拟合多元线性回归模型、选择最优模型，最终进行区间预测，定性的研究影响我国经济增长的主要因素。

二、试验的设计与数据收集过程

为了大致描绘改革开放以来我国经济的增长情况，原计划收集1978年至今的数据，但是全社会固定资产投资只有1980年之后的数据，所以最终只分析了自上个世纪八十年代以来的数据。影响国内生产总值GDP的因素有很多，本实验主要收集了1980-2018年进出口总额、金融机构资金来源流通中货币、社会消费品零售总额和全社会固定资产投资的数据，数据单位都为亿元，数据来源：国家统计局移动门户网站。

三、数据的描述性分析

用GDP、EM、MO、Consumption、Investment分别代表国内生产总值(亿元)、进出口总额(亿元)、金融机构资金来源流通中货币(亿元)、社会消费品零售总额(亿元)和全社会固定资产投资(亿元)。其中，国内生产总值GDP代表我国的经济增长状况，是因变量，其他四个变量是影响经济增长的因素，都是自变量。首先编写一个函数通过样本的数字特征对样本进行一些初步的定性分析。


查看导入的数据：

四、数据分析

查看变量之间的相关性：可以用cor函数得出变量之间的相关系数矩阵，或者用scatterplotMatrix函数，直接绘制散点图矩阵来查看变量之间的相关性。
由相关系数矩阵结果我们可以看到各个变量之间的相关系数都达到了0.9以上，是高度线性相关的，可以拟合线性回归模型。

scatterplotMatrix函数默认在非对角线区域绘制变量间的散点图，并添加平滑和线性拟合曲线。spread=FALSE表示删除了残差正负均方根在平滑曲线上的展开和非对称信息。

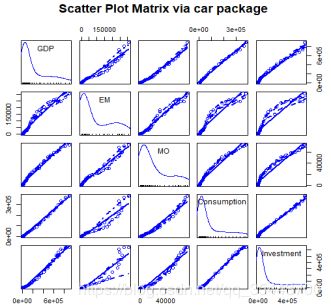
由变量间相关性实验结果，我们可以知道各个变量之间有正相关的线性关系，为了选择比较合适的解释变量，我们需要拟合以GDP为因变量、其他四个变量为自变量的多元回归模型。

用summary函数来查看模型的详细拟合结果：

Residuals列出了残差的最小值、四分之一分位数、中位数、四分之三分位数、最大值。Coefficients列出了每个自变量（包括截距项）的估计值、标准差、t值和P值（Pr(>|t|)）。可以看到在5%的显著性水平上，除了自变量MO不显著，其他自变量都是显著的。判断模型拟合效果的可决系数也叫判定系数R2的值，可以看到R2为0.995，非常接近于1，说明模型拟合效果很好。还有判断模型联合显著性的F统计量的值：F-statistic=1.808e+04,自由度为（4,34），p-value<2.2e-16，结果表面在1%的显著性水平下，模型是联合显著的。

计算方差分析表：

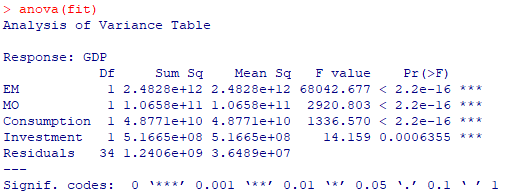
在确认回归模型之前要先进行假设检验，即回归模型的诊断。回归模型的诊断，最常用的的方法是使用plot函数。


ResidualsvsFitted图（左上）主要用于检验是否线性于参数，图中残差值和拟合值基本没有比较明显的关联，则说明自变量与因变量之间是线性关系。
NormalQ-Q图（右上）主要检验误差项的正态性，若满足正态性的假设，则图上的圆点应落在45度角的直线上；反之，则不满足正态性的假设。从图中结果来看，基本满足正态性的假设。
Scale-Location图（左下）主要检验误差的同方差性的假设，若水平线周围的点随机分布，则满足同方差假设；反之，则不满足。而观察此处结果，满足同方差性的假设。
ResidualsvsLeverage图（右下）主要用于观察数据中的单个值，不用于假设检验。

对于模型的最优选择问题，我们可以使用AIC来进行比较，它的原理是在可决系数与自变量的个数之间进行权衡，选择二者的最佳组合。AIC值越小，表明模型拟合效果越好。

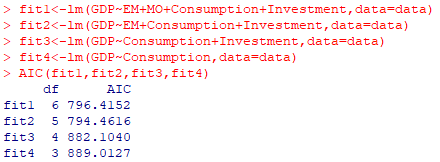
结果表明fit2的AIC值最小，拟合结果最好，即选择EM、Consumption、Investment三个变量为自变量的多元线性回归模型为最优模型。这与前面模型的详细拟合结果里MO的t检验结果不显著，而其他三个变量t检验结果显著刚好一致。

由以上实验结果表明选择影响GDP增长的因素主要有进出口总额、社会消费品零售总额以及全社会固定资产投资。重新拟合最优模型：


由此得出多元线性回归方程为：y=-1887+0.5565x1+2.263x2-2.283x3。
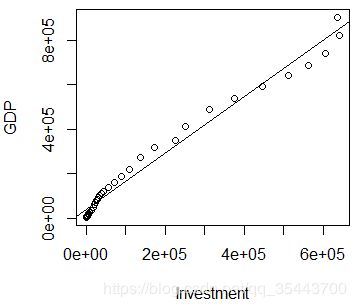
绘制自变量与因变量之间的散点图和拟合曲线：




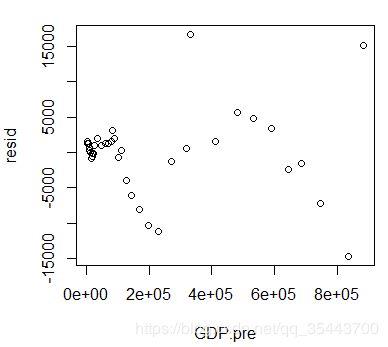
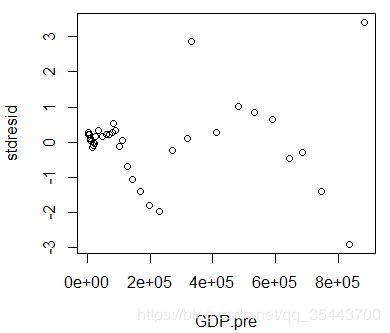
计算残差、标准化残差、计算预测值、画残差图、画残差QQ图：




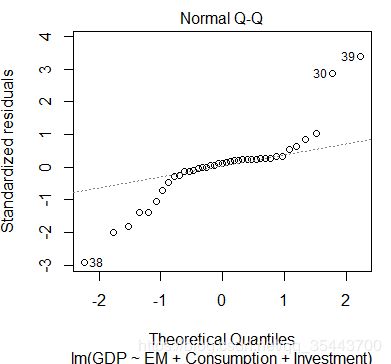
进行模型的预测，需要用到predict函数。实验数据为1980-2018年间的，假设2019年的EM为335000.00，Consumption=为400000.0，Investment为655000.00，可以预测到2019年的GDP的值为940344.7，95%的预测区间为（925188.7，955500.8）。

五、结论与讨论

通过本次实验得到了影响GDP增长的各种因素构成的多元线性回归方程：y=-1887+0.5565x1+2.263x2-2.283x3。该回归方程的截距项是-1887，EM每增加一个单位会引起GDP增加0.557个单位，Consumption每增加一个单位引起GDP增长2.263个单位，Investment每增加一个单位会引起GDP减少0.228个单位。也就是说，为了促进我国经济的快速发展，可以扩大对外开放程度来增加进出口总额，可以采取刺激消费、适当的减少投资从而促进经济增长。同时此次试验也可以在一定程度上对2019年的GDP进行预测，更好的掌握经济动向。

六、参考文献

[1]范金城, 梅长林. 2002. 数据分析. 北京: 科学出版社.
[2]薛毅, 陈立萍. 2007. 统计建模与R软件. 北京: 科学出版社.
[3]王斌会. 2010. 多元统计分析与R语言建模. 广州: 暨南大学出版社.
[4]李素兰.2017. 数据分析与R软件（第二版）.北京: 科学出版社.

附件1：数据

指标    国内生产总值 进出口总额	货币	社会消费品零售总额
2018年	900309.5	305008.13	73208	    380986.9
2017年	820754.3	278099.24	70645.6	    366261.6
2016年	740060.8	243386.46	68303.87	332316.3
2015年	685992.9	245502.93	63216.58	300930.8
2014年	641280.6	264241.77	60259.53	271896.1
2013年	592963.2	258168.89	58574.44	242842.8
2012年	538580	    244160.21	54659.77	214432.7
2011年	487940.2	236401.95	50748.46	187205.8
2010年	412119.3	201722.34	44628.17	158008
2009年	348517.7	150648.06	38245.97	133048.2
2008年	319244.6	179921.47	30218.96	114830.1
2007年	270092.3	166924.07	30334.32	93571.6
2006年	219438.5	140974.74	27072.62	79145.2
2005年	187318.9	116921.77	24031.67	68352.6
2004年	161840.2	95539.09	21468.3	    59501
2003年	137422	    70483.45	19745.99	52516.3
2002年	121717.4	51378.15	17278.03	48135.9
2001年	110863.1	42183.62	15688.8	    43055.4
2000年	100280.1	39273.25	14652.65	39105.7
1999年	90564.4	    29896.23	13455.5	    35647.9
1998年	85195.5	    26849.68	11204.15	33378.1
1997年	79715	    26967.24	10177.61	31252.9
1996年	71813.6	    24133.86	8802.01	    28360.2
1995年	61339.9	    23499.94	7885.34	    23613.8
1994年	48637.5	    20381.9	    7288.6	    18622.9
1993年	35673.2	    11271.02	5864.7	    14270.4
1992年	27194.5	    9119.62	    4336	    10993.7
1991年	22005.6	    7225.75	    3177.8	    9415.6
1990年	18872.9	    5560.12	    2644.87	    8300.1
1989年	17179.7	    4155.92	    2344.02	    8101.4
1988年	15180.4	    3821.79	    2134.03	    7440
1987年	12174.6	    3084.16	    1454.48	    5820
1986年	10376.2	    2580.37	    1218.36	    4950
1985年	9098.9	    2066.71	    987.83  	4305
1984年	7278.5	    1201.03	    792.11	    3376.4
1983年	6020.9	    860.15	    529.78	    2849.4
1982年	5373.4	    771.37	    439.12	    2570
1981年	4935.8	    735.34	    396.34	    2350
1980年	4587.6	    570.04	    346.2	    2140

附件2：代码

GDP<-c(4587.6,4935.8,5373.4,6020.9,7278.5,9098.9,10376.2,12174.6,15180.4,17179.7,18872.9,22005.6,27194.5,35673.2,48637.5,61339.9,71813.6,79715.0,85195.5,90564.4,100280.1,110863.1,121717.4,137422.0,161840.2,187318.9,219438.5,270092.3,319244.6,348517.7,412119.3,487940.2,538580.0,592963.2,641280.6,685992.9,740060.8,820754.3,900309.5)
EM<-c(570.00,735.34,771.37,860.15,1201.03,2066.71,2580.37,3084.16,3821.79,4155.92,5560.12,7225.75,9119.62,11271.02,20381.90,23499.94,24133.86,26967.24,26849.68,29896.23,39273.25,42183.62,51378.15,70483.45,95539.09,116921.77,140974.74,166924.07,179921.47,150648.06,201722.34,236401.95,244160.21,258168.89,264241.77,245502.93,243386.46,278099.24,305100.00)
MO<-c(346.20,396.34,439.12,529.78,792.11,987.83,1218.36,1454.48,2134.03,2344.02,2644.87,3177.80,4336.00,5864.70,7288.60,7885.34,8802.01,10177.61,11204.15,13455.50,14652.65,15688.80,17278.03,19745.99,21468.30,24031.67,27072.62,30334.32,30218.96,38245.97,44628.17,50748.46,54659.77,58574.44,60259.53,63216.58,68303.87,70645.60,73208.00)
Consumption<-c(2140.0,2350.0,2570.0,2849.4,3376.4,4305.0,4950.0,5820.0,7440.0,8101.4,8300.1,9415.6,10993.7,14270.4,18622.9,23613.8,28360.2,31252.9,33378.1,35647.9,39105.7,43055.4,48135.9,52516.3,59501.0,68352.6,79145.2,93571.6,114830.1,133048.2,158008.0,187205.8,214432.7,242842.8,271896.1,300930.8,332316.3,366261.6,380987.0)
Investment<-c(910.90,961.00,1230.40,1430.10,1832.90,2543.20,3120.60,3791.70,4753.80,4410.40,4517.00,5594.50,8080.10,13072.30,17042.10,20019.30,22913.50,24941.10,28406.20,29854.70,32917.73,37213.49,43499.91,55566.61,70477.40,88773.62,109998.20,137323.94,172828.40,224598.77,251683.77,311485.13,374694.74,446294.09,512020.65,561999.83,606465.66,641238.40,635636.00)

summarize <- function(x){
n <- length(x)
m <- mean(x)
v <- var(x)
s <- sd(x)
me <- median(x)
cv <- 100s/m
css <- sum((x-m)^2)
uss <- sum(x^2)
R <- max(x)-min(x)
R1 <- quantile(x,3/4)-quantile(x,1/4)
M3=quantile(x,1/4)(1/4)+me*(1/2)+ quantile(x,3/4)(1/4)
g1 <- n/((n-1)(n-2))sum((x-m)^3)/s3
g2 <- ((n(n+1))/((n-1)(n-2)(n-3))sum((x-m)^4)/s4- (3(n-1)^2)/((n-2)*(n-3)))
data.frame(N=n, Mean=m, Var=v, std_dev=s,Median=me, CV=cv, CSS=css, USS=uss,M3=M3,R=R, R1=R1, Skewness=g1, Kurtosis=g2, row.names=1)
}

data=data.frame(GDP=GDP,EM=EM,MO=MO,Consumption=Consumption,Investment=Investment)
data

cor(data)

scatterplotMatrix(data,spread=FALSE,main=“Scatter Plot Matrix via car package”)

fit<-lm(GDP~EM+MO+Consumption+Investment)
fit

summary(fit)

anova(fit)

par(mfrow=c(2,2))
plot(fit)
fit1<-lm(GDP~EM+MO+Consumption+Investment,data=data)
fit2<-lm(GDP~EM+Consumption+Investment,data=data)
fit3<-lm(GDP~Consumption+Investment,data=data)
fit4<-lm(GDP~Consumption,data=data)
AIC(fit1,fit2,fit3,fit4)

fitter<-lm(GDP~EM+Consumption+Investment,data=data)
summary(fitter)

coefficients(fitter)

ARsqured<-summary(fitter)$adj.r.squared
ARsqured

plot(GDP~EM)
abline(lm(GDP~EM))
plot(GDP~Consumption)
abline(lm(GDP~Consumption))
plot(GDP~Investment)
abline(lm(GDP~Investment))

resid<-residuals(fitter)
stdresid<-rstandard(fitter)
GDP.pre<-predict(fitter)
plot(GDP.pre,resid)
plot(GDP.pre,stdresid)
plot(fitter,2)

new<-data.frame(EM=(335000.00),Consumption=c(400000.0),Investment=c(655000.00))
lm.pred<-predict(fitter,new,interval=“prediction”,level=0.95)
lm.pred