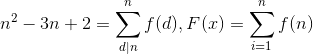杜教筛学习报告(随训练更新)

目录

关于杜教筛的简述

训练记录：

51nod1244 莫比乌斯函数之和

51nod1239 欧拉函数之和

bzoj3944 sum

hdu5608 Function

---

 

 

关于杜教筛的简述

看了skywalkert的博客大概明白了。

author: skywalkert 
original article: http://blog.csdn.net/skywalkert/article/details/50500009 
last update time : 2017-04-01

大体思路是如果能通过狄利克雷卷积构造一个更好计算前缀和的函数，且用于卷积的另一个函数也易计算，则可以简化计算过程。

构造函数后前 项的前缀和预处理出来，剩下的部分通过前面构造的函数进行递归。大概构造成：

这种形式，f(n)是待求前缀和，g(n)是构造的函数。然后进行递归。

特别注意！！！由于亚线性筛的复杂度低于O(n)所以一般数据范围是1e8-1e11，取模！！！一定注意取模！！！

前置技能：莫比乌斯反演，常用积性函数，线性筛

训练记录：

51nod1244 莫比乌斯函数之和

题意：求莫比乌斯函数的前缀和。

思路：由于数据范围是1e10，显然不能采用线性做法，采取杜教筛，构造一个函数满足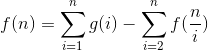，注意到莫比乌斯函数的性质,所以有,于是乎，我们构造g(n)=1.

然后式子就成了,然后预处理一下4e6范围的莫比乌斯函数的前缀和递归就完了，中间用map记录一下已计算的项减低复杂度。

复杂度：

#include 
using namespace std;
typedef long long ll;
const int N = 4641600;
const int inf = 0x3f3f3f3f;
const int mod = 1e6 + 3;
//const double pi = acos(-1.0);
const double eps = 1e-6;
const int inv = 5e8 + 4;
int gcd(int a,int b){return b ? gcd(b,a % b) : a;}
ll n,m;
int mu[N],prime[N],cnt;
bool vis[N];
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
void Mobius()
{
    cnt = 0;
    mu[1] = 1;mu[0] = 0;
    for(int i = 2; i < N; ++i){
        if(!vis[i]){
            prime[++cnt] = i;
            mu[i] = -1;
        }
        for(int j = 1; j <= cnt; ++j){
            if(i * prime[j] >= N) break;
            vis[i * prime[j]] = true;
            if(i % prime[j]== 0){
                mu[i * prime[j]] = 0;
                break;
            }
            mu[i * prime[j]] = -mu[i];
        }
        mu[i] += mu[i - 1];
    }
}
mapmp;
int work(ll jq)
{
    if(jq < N) return mu[jq];
    if(mp[jq]) return mp[jq];
    int res = 1;ll last;
    for(ll i = 2;i <= jq;i = last + 1){
        last = jq / (jq / i);
        res -= (last - i + 1) * work(jq / i);
    }
    mp[jq] = res;
    return res;
}
int main()
{
    Mobius();//cout << pow((ll)10000000000,2.0/ 3);
    n = read(),m = read();
    printf("%d\n",work(m) - work(n - 1));
    return 0;
}

---

51nod1239 欧拉函数之和

题意：求欧拉函数前缀和

思路：注意到欧拉函数的性质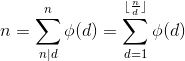,所以有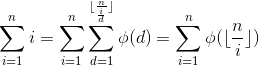,所以构造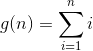,所以就变成了求解.

复杂度：

#include 
using namespace std;
typedef long long ll;
const int N = 4641600;
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + 7;
//const double pi = acos(-1.0);
const double eps = 1e-6;
const int inv = 5e8 + 4;
int gcd(int a,int b){return b ? gcd(b,a % b) : a;}
ll phi[N];
int prime[N],cnt;
bool isprime[N];
ll n;
inline ll add(ll x)
{
    return x >= mod ? x - mod : x;
}
inline ll sub(ll x)
{
    return x < 0 ? x + mod : x;
}
void get_phi()
{
   phi[1] = 1;
   for(int i = 2;i < N;++i){
       if(!isprime[i]){
             prime[++cnt] = i;
             phi[i] = i - 1;
        }
       for(int j = 1;j <= cnt && i * prime[j] < N;++j)
       {
          isprime[i * prime[j]] = 1;
          if(i % prime[j] == 0){
             phi[i * prime[j]] = phi[i] * prime[j];
             break;
          }
          else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
       }
   }
   for(int i = 2;i < N;++i) phi[i] = add(phi[i] + phi[i - 1]);
}

mapmp;
ll work(ll jq)
{
    if(jq < N) return phi[jq];
    if(mp[jq]) return mp[jq];
    ll res = jq % mod * ((jq + 1) % mod) % mod * inv % mod,last;
    for(ll i = 2;i <= jq;i = last + 1){
        last = jq / (jq / i);
        res = sub(res - (last - i + 1) * work(jq / i) % mod);
    }
    mp[jq] = res;
    return res;
}
int main()
{
    get_phi();
    scanf("%lld",&n);
    printf("%lld\n",work(n));
    return 0;
}

---

bzoj3944 sum

题意：求欧拉前缀和和莫比乌斯函数前缀和

思路：同上，注意开结构体避免栈溢出！！！

#pragma comment(linker, “/STACK:1024000000,1024000000”
#include 
using namespace std;
typedef long long ll;
const int N = 5e6 + 7;
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + 7;
//const double pi = acos(-1.0);
const double eps = 1e-6;
const int inv = 5e8 + 4;
int gcd(int a,int b){return b ? gcd(b,a % b) : a;}
ll phi[N];
int prime[N],cnt,mu[N];
bool isprime[N];
ll n;
void get_phi()
{
   phi[1] = 1;mu[1] = 1;mu[0] = 0;
   for(int i = 2;i < N - 2;++i){
       if(!isprime[i]){
             prime[++cnt] = i;
             phi[i] = i - 1;
             mu[i] = -1;
        }
       for(int j = 1;j <= cnt && i * prime[j] < N - 2;++j){
          isprime[i * prime[j]] = 1;
          if(i % prime[j] == 0){
             phi[i * prime[j]] = phi[i] * prime[j];
             mu[i * prime[j]] = 0;
             break;
          }
          phi[i * prime[j]] = phi[i] * (prime[j] - 1);
          mu[i * prime[j]] = -mu[i];
       }
       mu[i] += mu[i - 1];
   }
   for(int i = 2;i < N - 2;++i) phi[i] = phi[i] + phi[i - 1];
}
struct node{
    ll p;
    int m;
};
mapmp,mp1;
node work(ll jq)
{
    if(jq < N - 3) return (node){phi[jq],mu[jq]};
    if(mp[jq]) return (node){mp[jq],mp1[jq]};
    node res = (node){(jq & 1 ? jq : jq / 2) * (jq & 1 ? (jq + 1) / 2 : jq + 1),1},tmp;
    ll last;
    for(ll i = 2;i <= jq;i = last + 1){
        last = jq / (jq / i),tmp = work(jq / i);
        res.p -= (last - i + 1) * tmp.p;
        res.m -= (last - i + 1) * tmp.m;
    }
    if(!mp[jq]) mp[jq] = res.p;
    if(!mp1[jq]) mp1[jq] = res.m;
    return res;
}
int main()
{
    get_phi();
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%lld",&n);
        if(!n){
            printf("0 0\n");
            continue;
        }
        node r = work(n);
        printf("%lld %d\n",r.p,r.m);
    }
    return 0;
}

---

hdu5608 Function

题意：已知f(x)满足求F(x).

思路：看都整出想到莫比乌斯反演。令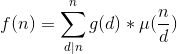,所以有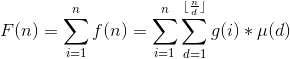,由前面莫比乌斯推的经验，我们直接构造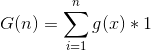,是不是突然清晰明了呢，这题就解决了。

//#pragma comment(linker, “/STACK:1024000000,1024000000”
#include 
using namespace std;
typedef long long ll;
const int N = 1e6 + 7;
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const int inv2 = 5e8 + 4;
//const double pi = acos(-1.0);
const double eps = 1e-6;
const int inv = 333333336;
int gcd(int a,int b){return b ? gcd(b,a % b) : a;}
int prime[N],cnt,mu[N];
ll g[N];
bool isprime[N];
ll n;
inline ll gao(ll x)
{
    return (x - 1) * (x - 2) % mod * x % mod * inv % mod;
}
void get_phi()
{
   mu[1] = 1;
   for(int i = 2;i < N;++i){
       if(!isprime[i]){
             prime[++cnt] = i;
             mu[i] = -1;
        }
       for(int j = 1;j <= cnt && i * prime[j] < N;++j){
          isprime[i * prime[j]] = 1;
          if(i % prime[j] == 0){
             mu[i * prime[j]] = 0;
             break;
          }
          mu[i * prime[j]] = -mu[i];
       }
       //mu[i] += mu[i - 1];
   }
   for(int i = 1;i < N;++i)
       for(int j = i;j < N;j += i)
           g[j] = ((g[j] + (ll)mu[j / i] * (i - 1) % mod * (i - 2) % mod) % mod + mod) % mod;
    for(int i = 2;i < N;++i) g[i] = (g[i] + g[i - 1]) % mod;
}
mapmp;
ll solve(ll pos)
{
    if(pos < N) return g[pos];
    if(mp[pos]) return mp[pos];
    ll res = gao(pos),last;
    for(ll i = 2;i <= pos;i = last + 1){
        last = pos / (pos / i);
        res = ((res - (last - i + 1) * solve(pos / i) % mod) % mod + mod) % mod;
    }
    mp[pos] = res;
    return res;
}
int main()
{
    get_phi();
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%lld",&n);
        printf("%lld\n",solve(n));
    }
    return 0;
}