森林与二叉树（数据结构）

题目描述

构造并实现森林的二叉树 ADT 和二叉树 ADT，森林 ADT 中应包括初始化、插入元素、删除元素，插入边，转换成二叉树，显示森林等基本操作，二叉 ADT 中应包括初始化、插入根、插入指定元素的左孩子或右孩子，转换成森林，显示二叉树等基本操作。

数据描述

第一行三个数 K, M, N。

• K : K∈{0,1}. 初始化ADT的类型, 0 表示接下来初始化森林, 1 表示初始化二叉树。
• M : M≤100. 初始化树的个数, 若 K=0, M 代表森林中树的个数. 若 K=1, M 一定为1。
• N : N≤5000. 初始化结点的个数, 若 K=0, N 表示森林中所有树的结点的数目之和, 若 K=1, N 表示二叉树中结点的个数。

接下来一行有 M 个数, 分别代表初始的根结点, 树中的结点均为正整数。
接下来 N 行, 表示森林、二叉树中的结点信息。

• 若初始为森林，每行的格式为 A B [nodes], 表示结点 A 拥有 B 个孩子结点, 孩子结点的集合为 nodes, i.e. 1 2 3 4 表示结点 1 拥有 2 个孩子, 分别为结点 3, 4。
• 若初始为二叉树，每行的格式为 A l r, 表示结点 A 的左孩子是 l, 右孩子是 r, 若是某个孩子不存在, 则其为值为 -1。

接下来一行一个数 Q (Q≤100), 表示接下来操作的个数。
接下来 Q 行, 每行的格式为 op [op_nums], 表示对当前森林/二叉树的操作, 下面是各种操作的格式:

• 1 father node 表示为森林中树的结点 father 插入一个孩子结点 node ，若 father 为 -1 , 表示插入的是孤立结点。 注意同一父亲的孩子从左至右按大小升序保存。
• 2 father node 表示删除森林中的结点 node , 其中 father 是 node 的父亲结点，father 若为 -1 ，代表删除根结点。若待删除的结点 node 有孩子, 则其所有孩子结点在删除后成为新的树, 保留其原有的子树结构。
• 3 a b 表示在森林中的根结点 a, b 间插入一条边, 其中 a 为 b 结点的父亲。
• 4 森林、二叉树转换, 若当前为森林，则将森林转为二叉树，若当前为二叉树，则将二叉树转为森林。当森林转换二叉树时, 将编号最小的根结点作为合并后的根结点, 其余根结点按从小到大合并。二叉树转森林时，无须恢复原有的树结构。
• 5 pos father node 表示为二叉树的 father 结点插入一个孩子 node , pos 的范围为{0, 1}, 0 表示插入的是 右孩子 , 1 表示插入的是 左孩子 . 数据保证 father 待插入的位置没有孩子。
• 6 显示森林/二叉树。显示二叉树时，输出一行二叉树的前序遍历序列的异或值。显示森林时，按森林根大小的顺序升序输出一行森林中各棵树的结点遍历序列的异或值，元素间用空格分隔。

Sample input & output

Sample input1

0 2 10
6 10 
6 0
10 3 2 8 5
2 1 9
8 0
5 3 4 3 1
4 0
9 0
3 1 7
7 0
1 0
10
6
6
6
1 -1 11
1 11 12
1 6 13
6
6
4
6

Sample output1

6 13 
6 13 
6 13 
11 13 7 
11 13 7 
1

Sample input2

1 1 15
7
1 3 9
2 -1 14
3 10 2
4 -1 12
5 -1 -1
6 -1 -1
7 1 4
8 -1 -1
9 -1 -1
10 11 5
11 -1 6
12 13 15
13 -1 8
14 -1 -1
15 -1 -1
8
5 1 5 16
6
6
6
6
6
4
6

Sample output2

16
16
16
16
16
4 18 9 15

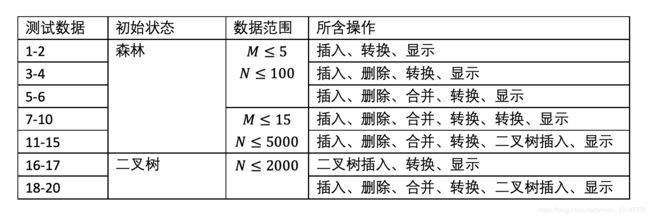
数据范围

思路

• 这个题，我森林用的二叉树来存的（左儿子右兄弟），森林类作为二叉树的派生类，这样就省去了森林转二叉树的过程，二叉树转森林也比较方便。
• 2号删除操作和3号连接操作都需要调整二叉树的结构，具体代码注释中有。
• 需要注意指针问题，容易指乱
• 森林还有另外一种存法，就是一个父结点拥有一个孩子数组，这种方法推荐数组使用vector，因为这样删除操作和插入操作都比较方便，避免了手动移动数组。

完整代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

const int maxn=5110;
struct binaryTreeNode//二叉树结点
{
    int element;
    binaryTreeNode *leftChild,*rightChild;
    binaryTreeNode() {leftChild=rightChild=nullptr; element=0;}
    binaryTreeNode(const int& theElement){
        element=theElement;
        leftChild=rightChild=nullptr;
    }
    binaryTreeNode(const int& theElement,binaryTreeNode *theLeftChild,binaryTreeNode *theRightChild){
        element=theElement;
        leftChild=theLeftChild;
        rightChild=theRightChild;
    }
};
class linkedBinaryTree//二叉树类
{
public:
    linkedBinaryTree(int _root=0){
        leaf=new binaryTreeNode*[maxn];
        for (int i=0; i<maxn; i++) leaf[i]=nullptr;
    }
    void init(int _root){
        leaf[_root]=new binaryTreeNode(_root);
        root=leaf[_root];
    }
    void insert(int father,int node,int lr);
    void insert_l_r(int father,int left,int right);
    int showTheBinaryTree(binaryTreeNode *t);
    void preorder(binaryTreeNode *t,int &ans);
    binaryTreeNode* getTheRoot(){return root;}
    void output(binaryTreeNode* t);
    binaryTreeNode* binaryTree_to_forest();
    void copy1(binaryTreeNode *node);
    void to_be_forest(binaryTreeNode *t);
protected:
    binaryTreeNode* root;
    binaryTreeNode** leaf;
};
void linkedBinaryTree::copy1(binaryTreeNode *node)
{
    if(node!=nullptr){
    if(leaf[node->element]==nullptr) leaf[node->element]=node;
        copy1(node->leftChild);
        copy1(node->rightChild);
    }
}
void linkedBinaryTree::to_be_forest(binaryTreeNode *t)
{
    root=t;
    copy1(root);
}
binaryTreeNode* linkedBinaryTree::binaryTree_to_forest()
{
    if(root->element!=0){//如果是一棵崭新的二叉树
        leaf[0]=new binaryTreeNode(0);//新建立一个0号结点
        leaf[0]->leftChild=root;
        root=nullptr;
    }
    return leaf[0];
}
void linkedBinaryTree::insert(int father, int node, int lr)
{
    if(leaf[father]==nullptr) leaf[father]=new binaryTreeNode(father);
    leaf[node]=new binaryTreeNode(node);
    if(lr) leaf[father]->leftChild=leaf[node];
    else leaf[father]->rightChild=leaf[node];
}
void linkedBinaryTree::insert_l_r(int father, int left, int right)
{
    if(leaf[father]==nullptr) leaf[father]=new binaryTreeNode(father);
    if(left!=-1) {
        if(leaf[left]==nullptr) leaf[left]=new binaryTreeNode(left);
        leaf[father]->leftChild=leaf[left];
    }
    if(right!=-1){
        if(leaf[right]==nullptr) leaf[right]=new binaryTreeNode(right);
        leaf[father]->rightChild=leaf[right];
    }
}
int linkedBinaryTree::showTheBinaryTree(binaryTreeNode *t)
{
    int ans=0;
    preorder(t,ans);
    return ans;
}
void linkedBinaryTree::preorder(binaryTreeNode *t, int &ans)
{
    if(t!=nullptr){
        ans^=t->element;
        preorder(t->leftChild,ans);
        preorder(t->rightChild,ans);
    }
}
void linkedBinaryTree::output(binaryTreeNode *t)
{
    if(t!=nullptr){
        cout<<t->element<<' ';
        if(t->leftChild!=nullptr) cout<<t->leftChild->element<<' ';
        else cout<<-1<<' ';
        if(t->rightChild!=nullptr) cout<<t->rightChild->element<<endl;
        else cout<<-1<<endl;
        output(t->leftChild);
        output(t->rightChild);
    }
}
class Forest : public linkedBinaryTree//派生森林类
{
public:
    ~Forest(){
        for (int i=0; i<maxn; i++)
            if(leaf[i]!=nullptr && leaf[i]->element==i)
                delete leaf[i];
        delete[] leaf;
    };
    void insert(int father,int node);
    void init(int size,int *a);
    bool erase(int father,int node);
    void showTheForest();
    bool link(int first,int second);
    binaryTreeNode* forest_to_binaryTree();
    void to_be_binaryTree(binaryTreeNode* t);
};
void Forest::to_be_binaryTree(binaryTreeNode *t)//根据大小重新链接各个根结点
{
    root=t;
    copy1(root);
    binaryTreeNode* tempgrandson=nullptr;
    binaryTreeNode* tempnode=root->leftChild;
    if(tempnode!=nullptr && tempnode->rightChild!=nullptr){
        tempgrandson=tempnode->rightChild;
        tempnode->rightChild=nullptr;
        while(tempgrandson!=nullptr){
            tempnode=tempgrandson;
            tempgrandson=tempgrandson->rightChild;
            tempnode->rightChild=nullptr;
            Forest::insert(0,tempnode->element);
        }
    }
}
binaryTreeNode* Forest::forest_to_binaryTree()
{
    binaryTreeNode* temp=root;
    root=nullptr;
    return temp->leftChild;
}
void Forest::showTheForest()
{
    binaryTreeNode* templeaf=root->leftChild;
    while(templeaf!=nullptr){
        int temp=showTheBinaryTree(templeaf->leftChild)^templeaf->element;
        cout<<temp<<' ';
        templeaf=templeaf->rightChild;
    }
}
bool Forest::erase(int father,int node)
{
    if(father==-1) father=0;//删除根结点
    binaryTreeNode* tempnode=leaf[father]->leftChild;//初始化为father的大儿子，最终存储为要删除的结点
    binaryTreeNode* tempgrandson=nullptr;
    if(leaf[father]->leftChild==nullptr){//如果要删除的父亲点没有儿子,即node不存在
        return false;//删除失败
    }
    if(leaf[father]->leftChild->element==node){//删除的是大儿子
        binaryTreeNode* tempnode2=leaf[father]->leftChild;
        leaf[father]->leftChild=tempnode->rightChild;
        tempnode=tempnode2;
    }
    else {//删除的不是大儿子
        while(tempnode->rightChild!=nullptr && tempnode->rightChild->element!=node)
            tempnode=tempnode->rightChild;
        if(tempnode->rightChild==nullptr){//找不到，删除失败
            return false;
        }
        //tempnode->rightChild是要删除的结点
        binaryTreeNode* tempnode2=tempnode->rightChild;
        tempnode->rightChild=tempnode->rightChild->rightChild;
        tempnode=tempnode2;
    }
    //tempnode->leftChild这一串将要都成为新的树,tempnode是要删除的点
    binaryTreeNode* tempnewnode=tempnode;
    if(tempnode->leftChild!=nullptr){
        tempgrandson=tempnode->leftChild->rightChild;
        tempnode->leftChild->rightChild=nullptr;
        Forest::insert(0,tempnode->leftChild->element);
        while(tempgrandson!=nullptr){
            tempnode=tempgrandson;
            tempgrandson=tempgrandson->rightChild;
            tempnode->rightChild=nullptr;
            Forest::insert(0,tempnode->element);
        }
    }
    delete tempnewnode;
    return true;

}
void Forest::insert(int father, int node)
{
    if(leaf[father]==nullptr) leaf[father]=new binaryTreeNode(father);
    if(leaf[node]==nullptr) leaf[node]=new binaryTreeNode(node);//开新结点
    if(father==-1) father=0;
    if(leaf[father]->leftChild==nullptr) leaf[father]->leftChild=leaf[node];//左儿子还有空位置
    else {//已经有一个儿子了，剩下的需要化作father左儿子的右兄弟
        binaryTreeNode* templeaf=leaf[father]->leftChild;
        if(templeaf->element>node){//插入大儿子
            leaf[father]->leftChild=leaf[node];
            leaf[node]->rightChild=templeaf;
        }
        else {//不是大儿子
            while(templeaf->rightChild!=nullptr && templeaf->rightChild->element<node)
                templeaf=templeaf->rightChild;
            binaryTreeNode* templeaf2=templeaf->rightChild;
            templeaf->rightChild=leaf[node];
            leaf[node]->rightChild=templeaf2;
        }
    }
}
void Forest::init(int size, int *a)//初始化森林
{
    sort(a+1,a+size+1,greater<int>());//从大到小排序，每次插入更快
    leaf[0]=new binaryTreeNode(0);//森林的根设置为0
    root=leaf[0];
    for (int i=1; i<=size; i++)
        Forest::insert(0,a[i]);
}
bool Forest::link(int first, int second)
{
    binaryTreeNode* tempfirstleaf=root->leftChild;
    binaryTreeNode* tempsecondleaf=root->leftChild;
    //先找到first
    if(tempfirstleaf->element!=first){
        while(tempfirstleaf->rightChild!=nullptr && tempfirstleaf->rightChild->element!=first)
            tempfirstleaf=tempfirstleaf->rightChild;
        if(tempfirstleaf->rightChild==nullptr)//找不到first
            return false;
        tempfirstleaf=tempfirstleaf->rightChild;
    }
    //此时找到了first，开始找second，并断开联系
    if(tempsecondleaf->element==second){//大儿子就是second
        root->leftChild=root->leftChild->rightChild;
        tempsecondleaf->rightChild=nullptr;
    }
    else{
        while(tempsecondleaf->rightChild!=nullptr && tempsecondleaf->rightChild->element!=second)
            tempsecondleaf=tempsecondleaf->rightChild;
        if(tempsecondleaf->rightChild==nullptr) //找不到second
            return false;
        binaryTreeNode * tempnode2=tempsecondleaf->rightChild;
        tempsecondleaf->rightChild=tempsecondleaf->rightChild->rightChild;
        tempsecondleaf=tempnode2;
        tempsecondleaf->rightChild=nullptr;
    }
    Forest::insert(tempfirstleaf->element,tempsecondleaf->element);
    return true;
}
void outputplus(int k,linkedBinaryTree bt,Forest ft)
{
    cout<<"Show:"<<endl;
    if(k) bt.output(bt.getTheRoot());
    else ft.output(ft.getTheRoot());
    cout<<"End"<<endl;
}
int main()
{
    int K,M,N,Q; cin>>K>>M>>N;//K==0为森林，1为二叉树
    linkedBinaryTree binaryTree;
    Forest forest;

    int a[5001];
    if(K){//初始化二叉树
        int root; cin>>root;
        binaryTree.init(root);
    }
    else {//初始化森林
        for (int i=1; i<=M; i++) cin>>a[i];
        forest.init(M,a);
    }
    if(K==0){
        for (int i=1; i<=N; i++){//输入N行的节点父子信息
            int A,B;
            cin>>A>>B;//A节点有B个子节点
            for (int j=1; j<=B; j++){
                int x; cin>>x;
                forest.insert(A,x);
            }
            //outputplus(K,binaryTree,forest);
        }
    }
    else {
        for (int i=1; i<=N; i++){
            int A,l,r;
            cin>>A>>l>>r;
            binaryTree.insert_l_r(A,l,r);
        }
    }
    cin>>Q;
    for (int i=1; i<=Q; i++){
        int op; cin>>op;
        if(op==1){//为森林中树的结点father插入一个孩子结点node，若father为-1, 表示插入的是孤立结
            int father,node; cin>>father>>node;
            forest.insert(father,node);
        }
        else if(op==2){//删除森林中的结点node, 其中father是node的父亲结点，father若为-1，代表删除根结点
            int father,node; cin>>father>>node;
            forest.erase(father,node);
        }
        else if(op==3){//在森林中的根结点 a, b 间插入一条边, 其中 a 为 b 结点的父亲
            int aa,b; cin>>aa>>b;
            forest.link(aa,b);
        }
        else if(op==4){//森林<->二叉树转换
            if(K) {//二叉树转化为森林
                K=0; forest.to_be_binaryTree(binaryTree.binaryTree_to_forest());
            }
            else {//森林转化为二叉树
                K=1; binaryTree.to_be_forest(forest.forest_to_binaryTree());
            }
        }
        else if(op==5){//为二叉树的father结点插入一个孩子node, pos的范围为{0, 1}, 0 表示插入的是左孩子, 1 表示插入的是右孩子
            int father,pos,node; cin>>pos>>father>>node;
            binaryTree.insert(father,node,pos);
        }
        else if(op==6){//显示森林/二叉树
            if(K) cout<<binaryTree.showTheBinaryTree(binaryTree.getTheRoot());
            else forest.showTheForest();
            putchar('\n');
            //outputplus(K,binaryTree,forest);
        }
    }
    return 0;
}