Min220

【论文系列】光流/ LK光流/ FlowNet/ FlowNet2

今天重点介绍光流

首先介绍光流的idea inspiration，传统光流的估计方法，再介绍用CNN解决光流的思路--FlowNet以及FlowNet2（个人认为只是利用stack方式堆叠FlowNetS和FlowNetC，其中更出彩的可能在数据集与更适应的数据训练方法，当然，精度和速度的效果也更为出色，解决了小displacement的估计）。Let's START!

光流

第一次读光流的文章是很久以前，当时有个印象很深的例子，就是当你坐火车的时候往窗外开，原本固定的刚体的物体，由于相对参考系的运动，仿佛变成了一条条川流的线，如同光在流动。而且，不同距离的物体，例如近处的相邻铁轨，远处的天和云，不远处的房屋，其运动的速度不是完全一样的，也就是说，我们可以通过不同的视觉感觉速度，而判断这个物体的远近。

光流（optical flow）最早在1940s由Gibson的The Perception of the Visual World.提出的，其定义是，由物体/相机的运动引起的在连续帧之间的视在运动模式。它是一个矢量2D场，每个矢量是一个位移矢量，代表点从第一帧到第二帧的运动。

光流需要满足的条件假设：

物体的像素强度在连续帧之间不会改变
相邻像素间有相似的运动

---------------------------------------------------

推导：

考虑在第一帧的像素点, $\left ( dx,dy \right )$ 为在下一帧中的运动的位移，所以该点经过运动后在第二帧为 $I \left ( x+dx,y+dy,t+dt \right )$ 。考虑到假设条件一，“物体的像素强度在连续帧之间不会改变”，有：

$I\left ( x ,y ,t \right )= I\left ( x+dx,y+dy,t+dt \right )$

将， $I\left ( x+dx,y+dy,t+dt \right )$ 泰勒展开：

$I\left ( x+dx,y+dy,t+dt \right ) = I\left ( x ,y ,t \right ) +\frac{\partial I}{\partial x}*dx+\frac{\partial I}{\partial y}*dy+\frac{\partial I}{\partial t}*dt+H.O.T.$

故有：

$\frac{\partial I}{\partial x}*dx+\frac{\partial I}{\partial y}*dy+\frac{\partial I}{\partial t}*dt = 0 \ \overset{\div dt} {\rightarrow}\ \ \frac{\partial I}{\partial x}*\frac{ dx}{ dt}+\frac{\partial I}{\partial y}*\frac{dy}{ dt}+\frac{\partial I}{\partial t} = 0$

其中 $\frac{ dx}{ dt},\ \frac{dy}{ dt}$ ，各代表其在x y方向的运动速度，可以看成 u，v。 $u= \frac{ dx}{ dt},\ v= \frac{dy}{ dt}$

这样我们就得到了光流方程

$f_{x}u+f_{y}v+f_{t}=0\ \ \ \leftarrow (f_{x}=\frac{\partial I}{\partial x}\, \ f_{y}=\frac{\partial I}{\partial y}\ \ f_{t}=\frac{\partial I}{\partial t})$

在这个光流方程中 $f_{x},\, f_{y}$ 代表的是图像在(x ,y,t )这一点的梯度， $f_{t}$ 是两帧图像块之间差值，均为已知。我们需要求解的u，v，那么如何求解呢？这里引入L-K光流法和L-K金字塔光流法。

L-K光流法

-------------------------------------------

稀疏光流法： L-K光流

利用L-K法解决光流，充分利用了光流的第二个假设条件，即，相邻像素间有相似的运动。需要注意的是，L-K光流法解决的是小位移情况，所以后文将会介绍L-K金字塔光流法来搞定大位移的光流问题。

由光流方程我们可知，现需求解两个未知数u&v。

L-K方法是找一个3*3的patch，利用相邻像素间有相似的运动，所以假定这九个点都有相同的位移。这样我们就可以得到方程组：

$\left\{\begin{matrix}f_{x1}u+f_{y1}v+f_{t1}=0 \\ f_{x2}u+f_{y2}v+f_{t2}=0 \\.... \\f_{x9}u+f_{y9}v+f_{t9}=0 \end{matrix}\right. \ \ \rightarrow \begin{bmatrix} f_{x1}&f_{y1} \\ f_{x2}&f_{y2} \\ ... \\ f_{x9}& f_{y9} \end{bmatrix} \cdot \begin{bmatrix} u\\ v \end{bmatrix} =- \begin{bmatrix} f_{t1}\\ f_{t2} \\ ... \\ f_{t9} \end{bmatrix}$
九个方程解两个未知数，超定，可以用最小二乘法来得出近似解。 $A\cdot \overrightarrow{x} =\overrightarrow{b}$

$\overrightarrow{x}= (A^{T}A)^{-1}A^{T}(-\overrightarrow{b}) \rightarrow \begin{bmatrix} u\\v \end{bmatrix} = \begin{bmatrix} \sum f_{xi}^{2} &\sum f_{xi}f_{yi} \\ \sum f_{xi}f_{yi}& \sum f_{yi}^{2} \end{bmatrix}^{-1} \begin{bmatrix} -\sum f_{xi} f_{ti} \\ -\sum f_{yi} f_{ti} \end{bmatrix}$

由此，我们解得x，但是观察

$\left ( A^{T} A\right )= \begin{bmatrix} \sum f_{xi}^{2} &\sum f_{xi}f_{yi} \\ \sum f_{xi}f_{yi}& \sum f_{yi}^{2} \end{bmatrix}$ ，并不一定总是可逆的！(充要条件 $\pmb{ \left | G \right | \neq 0\Leftrightarrow G \ is \ invertible }$ ）

在图像中沿着两个方向都有像素变化的区域（角点，这个式子也很像harris corner的响应式），一般对应的 $\left ( A^{t} A\right )$ 是可逆的，但是对于在灰度变化很小的区域，一般 $\left ( A^{t} A\right )$ 是不可逆的。这限制了LK光流法的适用范围，所以我们称之为稀疏光流法（并不是所有光流都能被计算出来）

在光流跟踪中，由于可逆的充要条件 $\pmb{ \left | G \right | \neq 0\Leftrightarrow G \ is \ invertible }$ ，也就是要求，矩阵G的最小特征值要足够大，满足这个要求的像素点才易于光流跟踪。）

-------------------------------------------

稠密光流法：迭代求解L-K光流

这里对上面的证明，再重新梳理一遍，并用迭代的方式求解光流d；连续帧 $I_{1},I_{2}$ ，对于 $I_{1}$ 中的像素点 $a = [x_{a},y_{a}]^{T}$ ,需要在 $I_{2}$ 中找到其对应的像素点 $b, \ b = a + d = [x_{a}+dx,y_{a}+dy]^{T}$ ,使得其灰度值差别最小（光流假设条件一：物体的像素强度在连续帧之间不会改变）。我们把图像在 $a = [x_{a},y_{a}]^{T}$ 处的运动位移 $d = [dx, dy]^{T}$ 称之为在a处的光流。又由条件二知道，相邻像素间光流相同，引入大小为 $w_{x},w_{y}$ 的相同光流邻域。

则求解转换为使下述目标函数的最小值优化为题：

$\varepsilon \left ( d \right ) = \varepsilon(d_{x},d_{y}) = \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}}\left ( I_{1}(x,y) - I_{2}(x+dx,y+dy) \right )^{2}$

一般来说，如果 $\epsilon \left ( d \right )$ 是一个数学形式很简单的函数，可以用解析形式来求——令目标函数的导数为0：

将 $I_{2}(x+dx,y+dy)$ 一阶泰勒展开，得到：

$\frac{\partial \epsilon \left ( d \right )}{\partial d} \approx -2 \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}}\left ( I_{1}(x,y) - I_{2}(x,y) -\begin{bmatrix} \frac{\partial I_{2}}{\partial x}&\frac{\partial I_{2}}{\partial y} \end{bmatrix}\begin{bmatrix} dx\\dy \end{bmatrix} \right )*\begin{bmatrix} \frac{\partial I_{2}}{\partial x}&\frac{\partial I_{2}}{\partial y} \end{bmatrix}$

由于 $d = [dx, dy]^{T}$ 足够小，有 $\begin{bmatrix} \frac{\partial I_{2}}{\partial x}&\frac{\partial I_{2}}{\partial y} \end{bmatrix} =\begin{bmatrix} \frac{\partial I_{1}}{\partial x}&\frac{\partial I_{1}}{\partial y} \end{bmatrix}$ ，且令 $\delta I=I_{1}(x,y)-I_{2}(x,y)$ ， $\bigtriangledown I =\begin{bmatrix} \frac{\partial I_{1}}{\partial x}&\frac{\partial I_{1}}{\partial y} \end{bmatrix}^{T}$ ，则有：

又 $\left( \bigtriangledown I^{T} d-\delta I \right )$ 为标量，有

$\begin{bmatrix} \frac{1}{2} \frac{\partial \varepsilon \left ( d \right ) }{\partial d} \end{bmatrix}^{T} \approx \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}} \left ( \bigtriangledown I^{T} d-\delta I \right )\bigtriangledown I \\ = \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}} \begin{bmatrix} f_{x}^{2} &f_{x}f_{y} \\ f_{x}f_{y} & f_{y}^{2} \end{bmatrix} d - \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}}\begin{bmatrix} \delta I \cdot f_{x}\\ \delta I\cdot f_{y} \end{bmatrix}$

再令

$G= \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}} \begin{bmatrix} f_{x}^{2} &f_{x}f_{y} \\ f_{x}f_{y} & f_{y}^{2} \end{bmatrix} ,\ \ b = \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}}\begin{bmatrix} \delta I \cdot f_{x}\\ \delta I\cdot f_{y} \end{bmatrix}$

因为我们最终是求得在使得导数=0下d的值， $d = G^{-1}b$ 。现在以迭代方式求解：

代表迭代次数（ $K \geq 1$ ），对于第k次迭代， $K\geq k\geq 2$ ，第k-1次迭代已经提供了初始值 $d^{k-1} = \begin{bmatrix} dx^{k-1} & dy^{k-1} \end{bmatrix}^{T}$ 并把该值作为图像 $I_{k}$ 处的运动位移初始值，移动后的点落在图像 $I_{k+1}$ ，则有 $I_{k+1} (x,y)= I_{k}(x+dx^{k-1},y+dy^{k-1})$ ，之后重复之前推导的内容： $\eta^{k}=\begin{bmatrix} \eta_{x}^{k}& \eta_{x}^{k} \end{bmatrix} ^{T}$ ，使得下面的目标函数最小：

$\varepsilon^{k} \left ( \eta ^{k} \right ) = \varepsilon^{k} (\eta_{x}^{k}, \eta_{x}^{k}) = \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}}\left ( I_{1}(x,y) - I_{k}(x+\eta_{x}^{k},y+\eta_{y}^{k}) \right )^{2}$

最终可以得到 $\eta_{x}^{k}=G^{-1}b_{k}$ (*这里的G在迭代计算中始终保持不变， $G= \sum_{x=x_{a}-w_{x}}^{x_{a}+w_{x}} \sum_{y=y_{a}-w_{y}}^{y_{a}+w_{y}} \begin{bmatrix} f_{x}^{2} &f_{x}f_{y} \\ f_{x}f_{y} & f_{y}^{2} \end{bmatrix}$ )而 $b_{k}$ 每次需要重新计算。

第k次迭代的结果 $d_{k}=d_{k-1}+\eta_{k}$ 。当迭代次数达到设定次数，或者计算得到的 $\eta^{k}$ 达到阈值，迭代计算结束。

金字塔光流法

我们知道L-K光流法中的几个假设都是强假设，当连续帧物体的运动位移较大（运动速度较快时）算法误差较大，如何解决？缩小图像尺寸，我们就可以使得运动像素变小。金字塔分层解决光流方法应用而生。简答来说，上层金字塔（低分辨率）图像中的一个像素可以代表下层的两个像素。利用金字塔的结构，可以自上而下修正光流运动位移。

步骤：

1.金字塔建立。首先，对两帧建立高斯金字塔，最低分辨率图在最顶层，原始图片在底层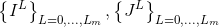： $\left \{ I^{L} \right \}_{L=0,...,L_{m}}, \left \{ J^{L} \right \}_{L=0,...,L_{m}}$ 。为了保证每层分解得到的图像尺寸都是整数，所以需要在正式处理之前，通过resize对原图像（包括前后两帧图像）的尺寸进行调整。

图像的金字塔化包括两个步骤：

①利用低通滤波器（lowpass filter）平滑图像。

防止图像降采样后发生锯齿现象。一般使用高斯滤波器，所以也称高斯金字塔

②对平滑图像进行抽样，从而得到一系列尺寸缩小的图像

可以对原始图像调整宽高以满足整除 $2^{L}$ ，也可以用公式确定新图像的宽高： $n_{x}^{L}\leq \frac{n_{x}^{L-1}+1}{2}, n_{y}^{L}\leq \frac{n_{y}^{L-1}+1}{2}$ 。 $n_{x}^{L} ,n_{y}^{L}$ 代表第L层图像的宽和高。

2.计算每层图像的光流，先计算顶层光流，从顶层（Lm层）开始，对于每一层L，通过最小化每个点的领域范围内的匹配误差和，得到顶层图像中每个点的光流。（g为上一层传递的初始值，d为光流位移与初始值的残差，即g+d=光流）

最小化该式→： ${\color{Red} \varepsilon^{L} \left ( d^{L} \right ) = \varepsilon^{L}(d_{x}^{L},d_{y}^{L}) = \sum_{x=x_{a}^{L}-w_{x}}^{x_{a}^{L}+w_{x}} \sum_{y=y_{a}^{L}-w_{y}}^{y_{a}^{L}+w_{y}}\left ( I^{L}(x,y) - J^{L}(x+g_{x}^{L}+dx^{L},y+g_{y}^{L}+dy^{L}) \right )^{2}}$

具体步骤如下：

①计算对于当前图像 $I^{L}$ 中像素点u对应的位置： $u^{L}=\begin{bmatrix} u^{L}_{x} & u^{L}_{y} \end{bmatrix}=\frac{u}{2^{L}}$ (图像缩放1/2)。

②计算图像 $I^{L}$ 在x方向的梯度： $f_{x}^{L}(x,y) = \frac{I^{L}(x+1,y)-I^{L}(x-1,y)}{2}\ ,u_{x}^{L}=x\ \&\ u_{y}^{L}=y$

③计算图像 $I^{L}$ 在y方向的梯度： $f_{y}^{L}(x,y) = \frac{I ^{L}(x ,y+1)-I^{L}(x,y-1)}{2}\ ,u_{x}^{L}=x\ \&\ u_{y}^{L}=y$

④计算空间矩阵G：

$G= \sum_{x=u_{x}^{L}-w_{x}}^{x=u_{x}^{L}+w_{x}} \sum_{y= u_{y}^{L}-w_{y}}^{ y=u_{y}^{L}+w_{y}} \begin{bmatrix} f_{x}^{L^{2}} &f_{x}^{L}f_{y}^{L} \\ f_{x}^{L}f_{y}^{L} & f_{y}^{L^{2}} \end{bmatrix}$

⑤迭代获取LK初始值g，最顶层的光流估计值设为0， $g^{L_{m}} = \begin{bmatrix} 0& 0 \end{bmatrix}^{T}$ ，其余层的光流估计值为： $g^{L-1} = 2 (g^{L}+d^{L})$

⑥计算图像差异：

$b = \sum_{x=u_{x}^{L}-w_{x}}^{x=u_{x}^{L}+w_{x}} \sum_{y= u_{y}^{L}-w_{y}}^{ y=u_{y}^{L}+w_{y}} \begin{bmatrix} \delta I^{k} \cdot f_{x}\\ \delta I^{k} \cdot f_{y} \end{bmatrix}, \\ where\ \delta I^{k} = I^{L}(x,y)- J^{L}(x+g_{x}^{L}+dx^{k-1},y+g_{y}^{L}+dy^{k-1})$

⑦计算残差向量 $\eta_{x}^{k}=G^{-1}b_{k}$ 。

⑧计算光流： $d^{k} = g^{k}+\eta ^{k}$ ，第L层的光流优化值 $d^{L}= d^{k}$

⑨提供下一层的光流计算的初始值，

$g^{L-1} = 2 (g^{L}+d^{L})$ 。

（假设图像的尺寸每次缩放为原来的1/2。共缩放了Lm层，第0层为原图。设已知原图的位移为d，则每层的位移为: $d^{L}=\frac{d}{2^{L}}$ ）

反馈直到底层(准确值=估计值+残差)

$d = g^{0}+d^{0}$

其实可以看出，最终的光流值，就是所哟偶层的分段光流d的叠加：

$d=\sum_{L=0}^{L_{m}} 2^{L}d^{L}, d^{L}\ is \ the \ optical \ flow \ of \ the \ L\ Level$

最终得到图像J中的点坐标。

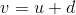光流金字塔实际操作中一些需要注意的点：

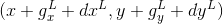$(x+g_{x}^{L}+dx^{L},y+g_{y}^{L}+dy^{L}) \right )$ 往往不是整数坐标，需要双线性插值。
滤波、求梯度时，需要注意图像边界处的像素点的关于像素越界的处理
v的坐标在J图像外被判定为错误点，但当v在J内时，匹配也不一定正确，需要滤除该方法计算得到的误匹配，常用解决方案是基于RANSAC计算两帧图像的变换矩阵。

至此，三个点推下来，相信你已经对光流有了比较深刻的理解了，接下来，我们将看如何利用CNN解决光流问题。

FlowNet

------------------------------------

文章下载地址：http://lmb.informatik.uni-freiburg.de/Publications/2015/DFIB15/
实现代码地址：http://lmb.informatik.uni-freiburg.de/resources/binaries/

FlowNet，开创了利用CNN来进行光流估计的先河。光流估计需要的两个条件：“needs precise per-pixel localization”，“requires finding correspondences between two input images”指向了利用CNN解决光流会面临的问题——要学习一个什么样的特征表达和如何匹配两图之间不同位置上的特征。作者提出的大致思路如下图所示：

首先，用两张图片作为输入，利用一个收缩部分（contracting part）压缩可用的信息，然后再利用一个放大部分（expanding part）将图像和光流特征图都恢复到full image resolution级别。并且在收缩部分，作者提出了两种网络结构FlowNetS(imple) 和FlowNetC(orrelation)，其区别在于FlowNetC中加入了一个新层——correlation layers——用来进行patch之间的乘性匹配（每两个patch都要一一匹配，后文细说），这个显式关联层，可以利用多层级多尺度和抽象的能力去学习强的特征来匹配（在FlowNet中没有完全发挥它的作用，是数据集和训练策略的问题，FlowNet2有提到，并且有更好地应用FlowNetC）。

网络结构

作者采用端到端的训练方式，整个网络结构中只用卷积层联系起来（读了上篇pooling博文的同学知道，没有连接层，就不用在意图片的输入大小。）在contracting part使用了池化操作使得计算更简单，网络不容易过拟合并且能够在输入图像大区域地聚集信息。但是Pooling会让网络分辨率降低，所以作者又加入了expanding part来refine收缩结果使得光流map最终可以以一个高像素图呈现。

收缩部分

收缩部分提出两个框架——FlowNetSimple 和 FlowNet Corr

FlowNetS

FlowNetS的思路很简单，我们就套用CNN在学习输入输出关系上很擅长的优点：我把一对图片的通道连接起来，网络结构图中可以看到输入的data层的channel是6输入，让网络自己去学习怎样处理图像对来获得光流移动信息，如上图所示，没有其他的多余操作。

整个收缩部分FlowNetS一共有九个卷积层，其中的六个stride（步长）为2。每一层后还有一个非线性的ReLU操作。卷积操作的filter大小随着网络的深入而递减。

FlowNetC

第二种方法是，将两张图片分开，两张图片经过同样的处理进行特征提取（我个人把卷积当做一个特征提取的过程），得到各自的feature map，再通过correlation layer使得这两张特征图在更高的特征级别（卷积后）上联系（匹配），再继续进行特征提取。整个过程就像图像匹配——提取特征+匹配特征，这里作者的匹配特征应用的方式是the correlation layers。

The correlation layers

既然要匹配“特征”了，那就是找最像的过程（别忘了光流的假设条件一：物体的像素强度在连续帧之间不会改变，所以找到最像像素的点对，motion就有了）。FlowNet作者的想法是，那我就把所有patch的对比结果都拿来做个map吧，继续在这个map上学习，我就能学到光流的。于是作者就先提出一个correlation（patchs相关性定义）：

描述一下这个公式，x1，x2是两张图的两个patch的中心坐标，二维， $x_{1}=\begin{bmatrix} a_{1} &b_{1} \end{bmatrix}, x_{2}=\begin{bmatrix} a_{2} &b_{2} \end{bmatrix}$ 。 $f_{1}, f_{2}$ 各自代表图像卷积后的feature map。每个patch的大小为K=2k+1，所以整个公式类似卷积核在图片上的卷积：以x1为中心的patch和以x2为中心的patch，对应位置相乘然后相加，但它的weight不可训练。

到这里，大家就会觉得如果两两patch都要算，会不会太麻烦？两块之间c*K*K的复杂度，考虑到光流本身是有一定的范围的，所以作者用两个小tips来解决计算的问题：

我假定光流是有最大displacement的，设定一个最大displacement范围d，超出x1中心d范围的patch，我不再做correlation比较。
加一个步长，s1和s2分别针对x1和x2，不用D范围（D=2d+1）都去进行计算。

于是乎，计算量得到减小，从correlation layers出来的结果维度为 $c(x_{1},x_{2}) = c(a_{1},b_{1},a_{2},b_{2}) = w*h*D^{2}$ 。

$for \ each \ point\ x1\ in \ f_{1}\ c(x_{1},*) = 1*1*D^{2}, the \ size \ of \ f_{1}=w*h \\so \c(x_{1},x_{2}) = c(a_{1},b_{1},a_{2},b_{2}) = w*h*D^{2}$

放大部分

放大部分主要由“upconvolutional layers”组成，主要进行unpooling和convolution操作。整个refinement过程如上图所示：作者在feature map上做反卷积（绿色箭头），同时将由收缩部分得到的feature map（灰色箭头）以及上采样得到的光流粗预测结果（红色箭头）连接起来(如果有的话)进行新的光流预测。每一步提升两倍的分辨率，重复四次，预测出来的光流的分辨率是输入图片的分辨率的1/4。如果想要继续提升分辨率，双线性插值没有什么明显地提升，可以用variational refinement。

至此，网络结构大概就已经被梳理好了，具体的其他细节，可以对照原文查看。

--------------------------------------------------------

数据集制作

这是本文的第二个贡献，作者通过拼接前景和背景制造的仿真数据集Flying Chairs使得网络能够有充分数据进行训练。具体做法、考量内容，本文不关注。此外，作者也比较了其他几个光流数据集的光流类型，数据集特点，有兴趣可以详读。

评价指标

EPE是一种对光流预测错误率的一种评估方式，代表所有像素点的gound truth和预测出来的光流之间差别距离（欧氏距离）的平均值，越低越好。

数据集表现：

Sintel Clean ： FlowNetC比FlowNetS要好。
Sintel Final：FlowNetS比FlowNetC要好。
Flyingchair：Flownet优于其他方法，FlowNetC比FlowNetS要好：
Kitti：Flownet表现一般，FlowNetS比FlowNetC要好。

FlowNetC比FlowNetS比较

数据集的表现上各有千秋，但是FlowNetC有过拟合的问题所以才导致有些数据集上的表现不够好。（可以继续看在FlowNet2上如何进行训练的改进。）相比FlowNetS，FlowNetC应该可以在真实数据集上有更好的表现，所以坚信C网络在保存信息上的优势，加以更丰富的数据和合理的训练方法，可以得到更好的结果。

因为我们在计算correlation的时候，为了减少计算的复杂度，所以我们设立了max displacement d，这使得，有一些超出d范围的光流motion没能被很好地学习以及在数据集中被测试出来，所以FlowNetC在large displacement上的表现比FlowNetS要差，比如在kitti数据集上，动态物体多，displacement大。

本文贡献：

CNN预测光流先河。虽然我们也能大概感觉到，作为第一个利用CNN解决光流的工作，作者的思路可以算是尝试性的（但一定尝试了多种方法），FlowNetS结构如其名的simple..C相比S添加了correlation layers。所以我相信在利用深度学习方面一定有更好的网络结构和切入点来解决光流问题，只是大家暂时被障目所以暂时还没有找到...
FlyingChairs数据集。数据集真的是个好东西，深度学习上数据集多重要就不说了，自己的数据集还能够很好地说明你的实验效果，能够多加引用...当然制作起来也是...比较耗费精力。

FlowNet2

接下来进入FlowNet2的世界。

横空出世的FlowNet，证明了的确可以用CNN完成对光流的估计，然而，对于small displacement问题和在真实数据集上的表现，FlowNet要逊色于传统方法。FlowNet的不足，是有原因的：例如对训练数据的需求，例如没有充分发挥FlowNetC中显式关联层correlation layers的作用，例如训练策略是否存在一些不足？可不可以结合FlowNetS和FlowNetC?这里，FlowNet2更关注训练数据和训练策略，为解决FlowNet的不足给出了答案。

依据摘要，文章的主要贡献有三：

本文提出了新的训练策略和新的训练数据。并且实验证明，这些的确可以影响实验结果。作者首先是发现如果单独使用越复杂的数据，将导致越差的结果。然后作者还发现，多个数据集的训练策略可以显著提高实验结果，使得correlation layer真正派上用场。
作者将FlowNetC和FlowNetS进行堆叠而得到新的网络 instead of promoting a new architecture, 。并且在网络中，对第二帧图像施加warp操作，使得localization更精确。并非通过调节stack的深度和单个成分的大小，得到许多网络变种来控制网络精度和计算资源中的平衡，速度范围在8fps~140fps。
提出一个专治small displacement的子网络和数据集，弥补上一版的不足。基于此数据集的特定网络只是对于真实世界中小运动有着良好的效果。为了对于任意位移都能达到最佳的性能，添加了一个网络来融合前面堆叠网络和小位移网络。

FlowNet2继承了FlowNet的优点：large displacement上表现很好（传统方法的劣势），光流域里的极小细节也能正确估计，还有对于特定场景里学习先验的潜力和运行速度快。同时，还能搞定small displacement和光流噪声问题，加速real-world中的应用发展。上个对比图，更清晰的边界，更平滑的结果。

数据集策略

1.数据集质量要高，这是监督训练成功的关键。

2.不同属性的训练的数据的出场顺序也很重要。

如此一来，FlowNetC比FlowNetS效果要好。最好的训练效果的顺序和数据集是：先在Chairs数据集上训练，然后仔仔Things3D上fine-tuning。

本文的三个学习率训练策略：

不同的学习率训练策略+不同的数据集训练顺序得出的不同结果：

--------------------------------------------------------

Stacking Networks

1.Stacking Two Networks for Flow Refinement堆叠两个网络：

输入两张图片只用FlowNetS网络堆叠，添加warp或不添加warp。

得到如下观察：

1）如果只堆叠网络不warp，堆叠网络易过拟合，在Sintel数据集上结果更差

2）stack和warp同时使用比较好。warp的确可以提高精度

3）Net1层加intermediate loss效果更好

4）固定第一个网络在warp操作之后训练第二个网络可以得到最佳的结果。

堆叠网络大小是原始网络的两倍，易过拟合。解决办法是网络一个接一个的训练。

实验结果如下

2.Stacking Multiply Diverse Networks堆叠不同种网络：FlowNetS+FlowNetC

这一节主要是进行不同种类和大小的网络的堆叠。设第一个网络为bootstrap网络，第二个网络用不同权重的新网络（运行时间上不会增加，但训练资源会增加）。这种情况下，作者认为顶层网络，可以在不同的步骤中表征不同的任务——这样，通过固定现有网络再一个接一个的添加新网络，stack针对某一任务就可以在更小的数据集上训练了。

同时，可以通过对通道数的减少从而对网络进行精简，最佳精简的尺寸是3/8。用大小写来区分网络中到底用了多少通道数。CSS比C要好，通道数更少网络参数少，速度快。

【论文系列】光流/ LK光流/ FlowNet/ FlowNet2_第14张图片

3/8的来历

---------------------------------------------

Small displacement network

作者想要捕获小运动的同时不丢失大运动→但是亚像素级motion上，噪声影响了光流的估计。→这是FlowNet本身的结构固有问题造成的→作者设计了网络图中右下角的FlowNet-SD，用以下改进解决：

修改filter的大小，7*7，5*5都用成3*3，更小，更平滑。
FlowNetS的第一层的stride=2变为1
在上采样前加了卷积层用了平滑噪声
重新做了数据集ChairsSDHom

-----------------------------------------------

最后的一些实验结果

做完这些总结之后，再回头看，并没有觉得FlowNet有多惊艳，但是第一个就是第一个，开天辟地，FlowNet2更像一篇工程性的文章，这里修修，那里改改，堆叠网络，做各种实验，隔了几年之后的FlowNet2，效果的确很好，背后的工作和努力肯定是值得人肯定的，但我还是坚信...光流有更合适的其他深度学习网络结构可以解决....卷积只是在做类似金字塔的工作，但是你有足够的数据量可以学习，金字塔不能保存这个权重信息，切入点暂时也没想法，期待未来读到更惊艳的文章吧！

参考博客：

https://my.oschina.net/u/3702502/blog/1815343
Mega_Li 的博客 https://blog.csdn.net/lwx309025167/article/details/80012199?utm_source=blogxgwz0
FlowNet——爆米花好美啊的博客 https://blog.csdn.net/u013010889/article/details/71189271
FlowNet2——lvhhh 的博客 https://blog.csdn.net/lvhao92/article/details/72899761
FlowNet2——bea_tree 的博客https://blog.csdn.net/bea_tree/article/details/67049373

你可能感兴趣的:(CV/统计,理论&算法,深度学习,论文系列)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
LocalDateTime 转 String igotyback java 开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类 qt 开发语言 sdl2 linux
需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
每日一题——第八十九题互联网打工人no1 C语言程序设计每日一练 c语言
题目：在字符串中找到提取数字，并统计一共找到多少整数，a123xxyu23&8889，那么找到的整数为123，23，8889//思想：#include#include#includeintmain(){charstr[]="a123xxyu23&8889";intcount=0;intnum=0;//用于临时存放当前正在构建的整数。boolinNum=false;//用于标记当前是否正在读取一个整
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
2019-08-08 65454
东莞家庭聚会出行旅游去哪里玩住？想起来有很久没有和家里人聚会啦，这次组织家人来到威廉古堡别墅轰趴，一大家子27个人，在别墅订了一天办，玩的非常的开心，小孩子玩游戏机，也很放心不会丢，我们就在唱歌、打麻将、打桌球一系列的活动，还准备小次等小孩生日在别墅举办，还可以给孩子做一个生日的策划
读书||陶新华《教育中的积极心理学》1—28 流水淙淙2022
读一本好书，尤如和一位高尚者对话，亦能对人的精神进行洗礼。但是若不能和实践结合起来，也只能落到空读书的状态。读书摘要与感想1、塞利格曼在《持续的幸福》一书中提出了幸福2.0理论，提出幸福由5个元素决定——积极情绪、投入的工作和生活、目标和意义、和谐的人际关系、成就感。2、人的大脑皮层在进行智力活动时，都伴有皮下中枢活动，对这些活动进行体验请假，并由此产生了情感解读。人的情绪情感体验总是优先于大脑的
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
MYSQL面试系列-04 king01299 面试 mysql 面试
MYSQL面试系列-0417.关于redolog和binlog的刷盘机制、redolog、undolog作用、GTID是做什么的？innodb_flush_log_at_trx_commit及sync_binlog参数意义双117.1innodb_flush_log_at_trx_commit该变量定义了InnoDB在每次事务提交时，如何处理未刷入（flush）的重做日志信息（redolog）。它
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
数据仓库——维度表一致性墨染丶eye 背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕，完整连接为：数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看，当一系列星型模型共享一组公共维度时，所涉及的维度称为一致性维度。当维度表存在不一致时，短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别，因为维度的差别，分析工作涉及的领域从简单到复杂，但是都是通过复杂的报表来弥补设计
Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redis bootstrap 数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
果然只有离职的时候，才有人敢说真话！ return2ok
今天公司出了神贴。今天中午吃饭，同事问我看了论坛上的神贴了吗？什么帖子？我问。同事显得很惊讶，你居然没看，现在那个帖子可能会成为年度最佳帖子。这么厉害？我等不及了，饭没吃完就快速的奔向办公室，打开公司论坛，我要一睹这个帖子的神奇。写这帖子的童鞋胆儿真肥。这哪里是一个帖子，这是很多个帖子，组成了一个系列。某人从公司文化、管理、人事、项目管理等多个方面分析了公司的概况，并抨击了公司的各种弊端，并提出了
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
女儿考研完报考雅思捡拾流年
是否我过于焦虑？会不会无形间让女儿觉得压力太大了啊。2022年对于我们家来说是不平常的一年。女儿今年大四，为了准备考研，暑假也没回家，年初去了学校到了年末才回家。女儿自己一个人面对考研，没有参加培训，大四学校作业论文等课业也多，她同时也是很努力复习考研的。在疫情开放很多羊的时期，女儿终于顺顺利利参加12月24、25号的考研，我们和家人都觉得女儿回家来要好好休息调养。可女儿回到家，我再查阅考研信息，
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
红手套节马小媛为中国城市环卫者公益发声：今天我手红疏狂君
#红手套节#公益活动，线头公益以及同多方资源的共同努力我们邀请到了线头公益大使马小媛马小媛，1993年5月3日出生于江苏省南京市，中国内地新生代女演员。2015年马小媛参演网剧《余罪》，饰演警校校花安嘉璐的闺蜜。2016年马小媛主演系列电影《丽人保镖》中女一号林欢馨，正式出道。此后，马小媛陆续接演了电视剧《警花与警犬2》，在网剧《你美丽李美丽》中担任女主角李美丽。拂晓，当你还在睡梦中时，这座城跟你
推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
多线程之——ExecutorCompletionService 阿福德
在我们开发中，经常会遇到这种情况，我们起多个线程来执行，等所有的线程都执行完成后，我们需要得到个线程的执行结果来进行聚合处理。我在内部代码评审时，发现了不少这种情况。看很多同学都使用正确，但比较啰嗦，效率也不高。本文介绍一个简单处理这种情况的方法：直接上代码：publicclassExecutorCompletionServiceTest{@TestpublicvoidtestExecutorCo
Java面试题精选：消息队列(二) 芒果不是芒 Java面试题精选 java kafka
一、Kafka的特性1.消息持久化：消息存储在磁盘，所以消息不会丢失2.高吞吐量：可以轻松实现单机百万级别的并发3.扩展性：扩展性强，还是动态扩展4.多客户端支持：支持多种语言（Java、C、C++、GO、）5.KafkaStreams（一个天生的流处理）:在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制：Kafka进行生产或者消费的时候会
用Python实现读取统计单词个数程序媛了了 python 游戏 java
完整实例代码：fromcollectionsimportCounterdefpythonit():danci={}withopen("pythonit.txt","r",encoding="utf-8")asf:foriinf:words=i.strip().split()forwordinwords:ifwordnotindanci:danci[word]=1else:danci[word]+=
数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列 C语言
文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
张芝华49天共修 - 草稿李娟AINI
祈禱、靜心、源代碼編程、觀想發願四根支柱，運用靈性能量的助力，讓夢想和渴望在最大向度中輕鬆實現。共修群指定书籍:1.能断金刚麦克格西2.新世界：灵性的觉醒埃克哈特·托尔3.爱是一切的答案芭芭拉迪安吉莉思4.完美的爱,不完美的关系约翰•威尔伍德5.爱的业力法则麦克格西6.漫画《金刚经》蔡志忠7.蔡志忠典藏国学漫画系列(套装共6册)作业:全部在共修群里完成，并请保存好自己的作业。l一周三次共修觉察作业
sql统计相同项个数并按名次显示朱辉辉33 java oracle
现在有如下这样一个表： A表 ID Name time ------------------------------ 0001 aaa 2006-11-18 0002 ccc 2006-11-18 0003 eee 2006-11-18 0004 aaa 2006-11-18 0005 eee 2006-11-18 0004 aaa 2006-11-18 0002 ccc 20
Android+Jquery Mobile学习系列-目录白糖_ JQuery Mobile
最近在研究学习基于Android的移动应用开发，准备给家里人做一个应用程序用用。向公司手机移动团队咨询了下，觉得使用Android的WebView上手最快，因为WebView等于是一个内置浏览器，可以基于html页面开发，不用去学习Android自带的七七八八的控件。然后加上Jquery mobile的样式渲染和事件等，就能非常方便的做动态应用了。从现在起，往后一段时间，我打算
如何给线程池命名 daysinsun 线程池
在系统运行后，在线程快照里总是看到线程池的名字为pool-xx，这样导致很不好定位，怎么给线程池一个有意义的名字呢。参照ThreadPoolExecutor类的ThreadFactory，自己实现ThreadFactory接口，重写newThread方法即可。参考代码如下： public class Named
IE 中"HTML Parsing Error:Unable to modify the parent container element before the 周凡杨 html 解析 error readyState
错误： IE 中"HTML Parsing Error:Unable to modify the parent container element before the child element is closed" 现象：同事之间几个IE 测试情况下，有的报这个错，有的不报。经查询资料后，可归纳以下原因。
java上传 g21121 java
我们在做web项目中通常会遇到上传文件的情况，用struts等框架的会直接用的自带的标签和组件，今天说的是利用servlet来完成上传。我们这里利用到commons-fileupload组件，相关jar包可以取apache官网下载：http://commons.apache.org/ 下面是servlet的代码： //定义一个磁盘文件工厂 DiskFileItemFactory fact
SpringMVC配置学习 510888780 spring mvc
spring MVC配置详解现在主流的Web MVC框架除了Struts这个主力外，其次就是Spring MVC了，因此这也是作为一名程序员需要掌握的主流框架，框架选择多了，应对多变的需求和业务时，可实行的方案自然就多了。不过要想灵活运用Spring MVC来应对大多数的Web开发，就必须要掌握它的配置及原理。　　一、Spring MVC环境搭建：（Spring 2.5.6 + Hi
spring mvc-jfreeChart 柱图(1) 布衣凌宇 jfreechart
第一步：下载jfreeChart包，注意是jfreeChart文件lib目录下的，jcommon-1.0.23.jar和jfreechart-1.0.19.jar两个包即可；第二步：配置web.xml; web.xml代码如下 <servlet> <servlet-name>jfreechart</servlet-nam
我的spring学习笔记13-容器扩展点之PropertyPlaceholderConfigurer aijuans Spring3
PropertyPlaceholderConfigurer是个bean工厂后置处理器的实现，也就是BeanFactoryPostProcessor接口的一个实现。关于BeanFactoryPostProcessor和BeanPostProcessor类似。我会在其他地方介绍。PropertyPlaceholderConfigurer可以将上下文（配置文件）中的属性值放在另一个单独的标准java P
java 线程池使用 Runnable&Callable&Future antlove java thread Runnable callable future
1. 创建线程池 ExecutorService executorService = Executors.newCachedThreadPool(); 2. 执行一次线程，调用Runnable接口实现 Future<?> future = executorService.submit(new DefaultRunnable()); System.out.prin
XML语法元素结构的总结百合不是茶 xml 树结构
1.XML介绍1969年 gml (主要目的是要在不同的机器进行通信的数据规范)1985年 sgml standard generralized markup language1993年 html(www网)1998年 xml extensible markup language
改变eclipse编码格式 bijian1013 eclipse 编码格式
1.改变整个工作空间的编码格式改变整个工作空间的编码格式，这样以后新建的文件也是新设置的编码格式。 Eclipse->window->preferences->General->workspace-
javascript中return的设计缺陷 bijian1013 JavaScript AngularJS
代码1： <script> var gisService = (function(window) { return { name:function () { alert(1); } }; })(this); gisService.name(); &l
【持久化框架MyBatis3八】Spring集成MyBatis3 bit1129 Mybatis3
pom.xml配置 Maven的pom中主要包括： MyBatis MyBatis-Spring Spring MySQL-Connector-Java Druid applicationContext.xml配置 <?xml version="1.0" encoding="UTF-8"?> &
java web项目启动时自动加载自定义properties文件 bitray java Web 监听器相对路径
创建一个类 public class ContextInitListener implements ServletContextListener 使得该类成为一个监听器。用于监听整个容器生命周期的，主要是初始化和销毁的。类创建后要在web.xml配置文件中增加一个简单的监听器配置，即刚才我们定义的类。 <listener> <des
用nginx区分文件大小做出不同响应 ronin47
昨晚和前21v的同事聊天，说到我离职后一些技术上的更新。其中有个给某大客户(游戏下载类)的特殊需求设计，因为文件大小差距很大——估计是大版本和补丁的区别——又走的是同一个域名，而squid在响应比较大的文件时，尤其是初次下载的时候，性能比较差，所以拆成两组服务器，squid服务于较小的文件，通过pull方式从peer层获取，nginx服务于较大的文件，通过push方式由peer层分发同步。外部发布
java-67-扑克牌的顺子.从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的.2-10为数字本身，A为1，J为11，Q为12，K为13，而大 bylijinnan java
package com.ljn.base; import java.util.Arrays; import java.util.Random; public class ContinuousPoker { /** * Q67 扑克牌的顺子从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。 * 2-10为数字本身，A为1，J为1
翟鸿燊老师语录 ccii 翟鸿燊
一、国学应用智慧TAT之亮剑精神A 1. 角色就是人格就像你一回家的时候，你一进屋里面，你已经是儿子，是姑娘啦，给老爸老妈倒怀水吧，你还觉得你是老总呢？还拿派呢？就像今天一样，你们往这儿一坐，你们之间是什么，同学，是朋友。还有下属最忌讳的就是领导向他询问情况的时候，什么我不知道，我不清楚，该你知道的你凭什么不知道
[光速与宇宙]进行光速飞行的一些问题 comsci 问题
在人类整体进入宇宙时代，即将开展深空宇宙探索之前，我有几个猜想想告诉大家仅仅是猜想。。。未经官方证实 1：要在宇宙中进行光速飞行，必须首先获得宇宙中的航行通行证，而这个航行通行证并不是我们平常认为的那种带钢印的证书，是什么呢？下面我来告诉
oracle undo解析 cwqcwqmax9 oracle
oracle undo解析2012-09-24 09:02:01 我来说两句作者：虫师收藏我要投稿 Undo是干嘛用的？ &nb
java中各种集合的详细介绍 dashuaifu java 集合
一，java中各种集合的关系图 Collection 接口的接口对象的集合 ├ List 子接口 &n
卸载windows服务的方法 dcj3sjt126com windows service
卸载Windows服务的方法在Windows中，有一类程序称为服务，在操作系统内核加载完成后就开始加载。这里程序往往运行在操作系统的底层，因此资源占用比较大、执行效率比较高，比较有代表性的就是杀毒软件。但是一旦因为特殊原因不能正确卸载这些程序了，其加载在Windows内的服务就不容易删除了。即便是删除注册表中的相应项目，虽然不启动了，但是系统中仍然存在此项服务，只是没有加载而已。如果安装其他
Warning: The Copy Bundle Resources build phase contains this target's Info.plist dcj3sjt126com ios xcode
http://developer.apple.com/iphone/library/qa/qa2009/qa1649.html Excerpt: You are getting this warning because you probably added your Info.plist file to your Copy Bundle
2014之C++学习笔记（一） Etwo C++Etwo Etwo iterator 迭代器
已经有很长一段时间没有写博客了，可能大家已经淡忘了Etwo这个人的存在，这一年多以来，本人从事了AS的相关开发工作，但最近一段时间，AS在天朝的没落，相信有很多码农也都清楚，现在的页游基本上达到饱和，手机上的游戏基本被unity3D与cocos占据，AS基本没有容身之处。so。。。最近我并不打算直接转型
js跨越获取数据问题记录 haifengwuch jsonp json Ajax
js的跨越问题，普通的ajax无法获取服务器返回的值。第一种解决方案，通过getson，后台配合方式，实现。 Java后台代码： protected void doPost(HttpServletRequest req, HttpServletResponse resp) throws ServletException, IOException { String ca
蓝色jQuery导航条 ini JavaScript html jquery Web html5
效果体验：http://keleyi.com/keleyi/phtml/jqtexiao/39.htmHTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <title>jQuery鼠标悬停上下滑动导航条 - 柯乐义<
linux部署jdk,tomcat,mysql kerryg jdk tomcat linux mysql
1、安装java环境jdk: 一般系统都会默认自带的JDK,但是不太好用，都会卸载了，然后重新安装。 1.1）、卸载：（rpm -qa :查询已经安装哪些软件包； rmp -q 软件包：查询指定包是否已
DOMContentLoaded VS onload VS onreadystatechange mutongwu jquery js
1. DOMContentLoaded 在页面html、script、style加载完毕即可触发，无需等待所有资源（image/iframe）加载完毕。（IE9+） 2. onload是最早支持的事件，要求所有资源加载完毕触发。 3. onreadystatechange 开始在IE引入，后来其它浏览器也有一定的实现。涉及以下 document , applet, embed, fra
sql批量插入数据 qifeifei 批量插入
hi，自己在做工程的时候，遇到批量插入数据的数据修复场景。我的思路是在插入前准备一个临时表，临时表的整理就看当时的选择条件了，临时表就是要插入的数据集，最后再批量插入到数据库中。 WITH tempT AS ( SELECT item_id AS combo_id, item_id, now() AS create_date FROM a
log4j打印日志文件如何实现相对路径到项目工程下 thinkfreer Web log4j 应用服务器日志
最近为了实现统计一个网站的访问量，记录用户的登录信息，以方便站长实时了解自己网站的访问情况，选择了Apache 的log4j,但是在选择相对路径那块卡主了，X度了好多方法(其实大多都是一样的内用，还一个字都不差的)，都没有能解决问题，无奈搞了2天终于解决了，与大家分享一下需求：用户登录该网站时，把用户的登录名,ip,时间。统计到一个txt文档里，以方便其他系统调用此txt。项目名
linux下mysql-5.6.23.tar.gz安装与配置笑我痴狂 mysql linux unix
1.卸载系统默认的mysql [root@localhost ~]# rpm -qa | grep mysql mysql-libs-5.1.66-2.el6_3.x86_64 mysql-devel-5.1.66-2.el6_3.x86_64 mysql-5.1.66-2.el6_3.x86_64 [root@localhost ~]# rpm -e mysql-libs-5.1

【论文系列】光流/ LK光流/ FlowNet/ FlowNet2

光流

L-K光流法

稀疏光流法： L-K光流

稠密光流法：迭代求解L-K光流

金字塔光流法

光流金字塔​​​​​实际操作中​​一些需要注意的点：

FlowNet

网络结构

FlowNet2

Stacking Networks

参考博客：

你可能感兴趣的:(CV/统计,理论&算法,深度学习,论文系列)

光流金字塔实际操作中一些需要注意的点：