猫眼面经汇总

• 一、Java
  • Collections
  • hashset源码
  • hashmap源码
  • hashset和hashmap的区别
  • hashmap、hashtable原理，1.7,1.8的区别
  • haspmap的底层实现put操作，扩容机制
  • currenthashmap如何解决线程安全,1.7版本以及1.8版本的不同
  • arraylist默认大小，如何扩展的
  • 什么情况下会有线程安全的问题，怎么解决
  • synchronized和reetrantlock锁
  • cas
  • volatitle
  • 线程池
  • 创建线程的方法
  • java的线程和操作系统的线程什么关系
  • 优先级队列，如何处理
  • hash冲突的解决方式，如何判断各个方式的优劣
  • 乐观锁 和悲观锁
  • 如何实现让一个线程等待其他线程完成后在执行
  • AQS同步器框架，countdowmlatch，cyclebarrier，semaphore，读写锁
  • 线程池的参数，各种线程池
  • string ，stringbuild，stringbuffer区别，string内部结构
  • 拆箱装箱的原理
  • Lambda表达式
  • 如何实现list和map
  • 锁以及锁的底层实现
  • 队列和栈由什么实现的
  • 重写和重载
• 二、JVM
  • 说说垃圾回收，回收算法
  • jvm内存分区
  • CMS垃圾收集器
  • 类加载机制和双亲委派模型，以及为什么要实现双亲委派模型
  • 虚拟机调优参数
• 三、数据结构与算法
  • 链表反转
  • 跳楼梯
  • 不用乘法实现乘法
  • 一个字符串找里面是否有重复的字符
  • 数组的最大连续子串和
  • 快排的思想，为什么是O(N)，每次的基准选择哪个
  • 最好情况下时间复杂度最低的是那种排序
  • 分层打印二叉树
  • 非递归方式实现二叉树的层序遍历
  • 非递归方式实现二叉树的中序遍历
  • 二叉树后序遍历
  • 如何判断链表有环
  • 冒泡排序，如何优化
  • 合并两个有序数组
  • 给一串数字，建最大堆，以及建堆的时间复杂度，然后就让手撕堆排序的代码
  • 找两字符串中都存在的元素
• 四、操作系统
  • 死锁产生的条件
  • 产生死锁后如何解决
  • 线程和进程的区别
  • 进程间的通信
  • 作业调度算法
• 五、网络
  • osi，为什么是7层？
  • tcp三次握手
  • tcp四次挥手
  • 为什么三次握手和四次挥手
  • http发送的包里面有什么
  • TCP/IP五层结构，每次层分别有哪些协议
  • TCP和UDP的区别
  • 如果网络情况不好，三次握手怎么保证认证
  • tcp拥塞控制机制，慢开始，拥塞避免，快重传，快恢复
  • 浏览器输入网址按下回车后执行的全过程
  • HTTP与HTTPS区别
  • session和cookie
• 六、数据库
  • 对于redis的认识
  • mysql索引了解
  • 数据库三大范式
  • 解释脏读，幻读，可重复读
  • redis是单线程还是多线程，分布式锁
  • 数据库隔离级别，每层级别分别用什么方法实现
  • 三级封锁协议,共享锁排它锁，mvcc多版本并发控制协议，间隙锁
  • b+树和b数的区别，b+数的具体结构
  • innnodb和myisam的区别，各自的b数索引叶子节点分别存储什么
  • 全文索引，索引什么时候会失效
  • 索引的优化，最左前缀原则
  • 事务的特性
• 七、设计模式
  • 会那些设计模式
• 八、框架
  • springboot介绍一下
  • @SpringBootApplication
  • aop和ioc理解和原理
  • 反射，cglib代理，动态代理，如何实现
  • springboot的启动流程
  • spring中bean的生命周期
  • springmvc执行流程
• 九、智力题
  • 甲有n个白球，m个黑球，乙有无数个黑球。从甲抽两个球，都是白的，放回甲，一白一黑，从乙拿出黑给甲，都是黑，放回一个给甲。问甲中最后剩下一白一黑的概率

 

一、Java

Collections

java.util.Collections 是一个包装类（工具类/帮助类）。它包含有各种有关集合操作的静态多态方法。此类不能实例化，就像一个工具类，用于对集合中元素进行排序、搜索以及线程安全等各种操作，服务于Java的Collection框架。

常用方法：

1. sort(Collection)方法的使用(含义：对集合进行排序)。
2. reverse()方法的使用(含义：反转集合中元素的顺序)。
3. shuffle(Collection)方法的使用(含义：对集合进行随机排序)。
4. fill(List list,Object o)方法的使用(含义：用对象o替换集合list中的所有元素)
5. copy(List m,List n)方法的使用(含义：将集合n中的元素全部复制到m中,并且覆盖相应索引的元素)。
6. min(Collection),min(Collection,Comparator)方法的使用(前者采用Collection内含自然比较法，后者采用Comparator进行比较)。
7. max(Collection),max(Collection,Comparator)方法的使用(前者采用Collection内含自然比较法，后者采用Comparator进行比较)。
8. indexOfSubList(List list,List subList)方法的使用(含义：查找subList在list中首次出现位置的索引)。
9. lastIndexOfSubList(List source,List target)方法的使用与上例方法的使用相同
10. rotate(List list,int m)方法的使用(含义：集合中的元素向后移m个位置，在后面被遮盖的元素循环到前面来)。移动列表中的元素，负数向左移动，正数向右移动
11. swap(List list,int i,int j)方法的使用(含义：交换集合中指定元素索引的位置)
12. binarySearch(Collection,Object)方法的使用(含义：查找指定集合中的元素，返回所查找元素的索引)。
13. replaceAll(List list,Object old,Object new)方法的使用(含义：替换批定元素为某元素,若要替换的值存在刚返回true,反之返回false)。

hashset源码

hashmap源码

HashMap源码解析（JDK1.8）

hashset和hashmap的区别

hashmap、hashtable原理，1.7,1.8的区别

HashMap源码解析（JDK1.8）

haspmap的底层实现put操作，扩容机制

HashMap源码解析（JDK1.8）

currenthashmap如何解决线程安全,1.7版本以及1.8版本的不同

ConcurrentHashMap源码解析（JDK1.8）

arraylist默认大小，如何扩展的

ArrayList默认大小为10，扩容为原先数组大小的1.5倍，再判断新数组容量是否够用和长度是否大于最大值，再调用Arrays.copyOf复制到新数组上。

    /**
     * 扩容，以确保它可以至少持有由参数指定的元素的数目
     *
     * @param minCapacity 所需的最小容量
     */
    private void grow(int minCapacity) {
        // 获取到ArrayList中elementData数组的内存空间长度
        int oldCapacity = elementData.length;
        // 扩容至原来的1.5倍
        int newCapacity = oldCapacity + (oldCapacity >> 1);
        // 再判断一下新数组的容量够不够，够了就直接使用这个长度创建新数组，
        // 不够就将数组长度设置为需要的长度
        if (newCapacity - minCapacity < 0)
            newCapacity = minCapacity;
        //若预设值大于默认的最大值检查是否溢出
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        // 调用Arrays.copyOf方法将elementData数组指向新的内存空间时newCapacity的连续空间
        // 并将elementData的数据复制到新的内存空间
        elementData = Arrays.copyOf(elementData, newCapacity);
    }

什么情况下会有线程安全的问题，怎么解决

互斥同步：推荐使用 synchronized 关键字进行同步, 在 concurrent包中有ReentrantLock类, 实现效果差不多. 还是推荐原生态的synchronized.

非阻塞同步：需要硬件指令完成.常用的指令有:

Test-and-Set

Fetch-and-Increment

Swap

Compare-and-Swap (CAS)

Load-Linked/Store-Conditional (LL/SC)

典型的应用在 AtomicInteger 中

无同步方案：将变量保存在本地线程中，就不会出现多个线程并发的错误了。

java中主要使用的就是ThreadLocal这个类。

synchronized和reetrantlock锁

cas

volatitle

volatile是变量修饰符，其修饰的变量具有可见性，Java的做法是将该变量的操作放在寄存器或者CPU缓存上进行，之后才会同步到主存，使用volatile修饰符的变量是直接读写主存，volatile不保证原子性，同时volatile禁止指令重排。

线程池

创建线程的方法

• 继承Thread类创建线程类，重写run方法，run方法就是代表线程需要完成的任务，调用线程对象的start()来启动该线程，线程类已经继承了Thread类，所以不能再继承其他父类。
• 实现Runnable接口创建线程类，定义Runnable实现类，重写run方法
• 实现Callable接口，重写call()方法，call()作为线程的执行体，具有返回值
• 线程池，使用线程池产生线程对象java.util.concurrent.ExecutorService、java.util.concurrent.Executors

java的线程和操作系统的线程什么关系

优先级队列，如何处理

hash冲突的解决方式，如何判断各个方式的优劣

1. 开放定址法
2. 链地址法
3. 再哈希法
4. 建立一个公共溢出区

乐观锁 和悲观锁

悲观锁：假定会发生并发冲突，则屏蔽一切可能违反数据完整性的操作

乐观锁：假定不会发生并发冲突，只在数据提交时检查是否违反了数据完整性（不能解决脏读问题）

如何实现让一个线程等待其他线程完成后在执行

1. 通过一个线程安全的全局变量来控制, 每个其他线程执行结束该全局变量减一, 该线程判断全局变量为0时再向下执行
2. 该线程分别其他子线程的对象, 然后对其他线程执行wait方法, 释放对其他线程对象的占用，其他线程在执行结束后, 获取自己线程对象的锁, 执行notify方法, 唤醒该线程
3. join方法
4. 使用 CountDownLatch

AQS同步器框架，countdowmlatch，cyclebarrier，semaphore，读写锁

线程池的参数，各种线程池

string ，stringbuild，stringbuffer区别，string内部结构

拆箱装箱的原理

在装箱的时候自动调用的是Integer的valueOf(int)方法。而在拆箱的时候自动调用的是Integer的intValue方法。

    public static Integer valueOf(int i) {
        if (i >= IntegerCache.low && i <= IntegerCache.high)
            return IntegerCache.cache[i + (-IntegerCache.low)];
        return new Integer(i);
    }
    public int intValue() {
        return value;
    }

Lambda表达式

Lambda 表达式，也可称为闭包。Lambda 允许把函数作为一个方法的参数（函数作为参数传递进方法中）。使用 Lambda 表达式可以使代码变的更加简洁紧凑。

如何实现list和map

锁以及锁的底层实现

队列和栈由什么实现的

重写和重载

二、JVM

说说垃圾回收，回收算法

jvm内存分区

程序计数器:记录正在执行的虚拟机字节码指令的地址（如果正在执行的是本地方法则为空）。

Java虚拟机栈:每个 Java 方法在执行的同时会创建一个栈帧用于存储局部变量表、操作数栈、常量池引用等信息。每一个方法从调用直至执行完成的过程，就对应着一个栈帧在 Java 虚拟机栈中入栈和出栈的过程。

本地方法栈:与 Java 虚拟机栈类似，它们之间的区别只不过是本地方法栈为本地方法服务。

Java堆:几乎所有对象实例都在这里分配内存。是垃圾收集的主要区域（"GC 堆"），虚拟机把 Java 堆分成以下三块：

• 新生代
• 老年代
• 永久代

新生代又可细分为Eden空间、From Survivor空间、To Survivor空间，默认比例为8:1:1。

方法区：方法区（Method Area）与Java堆一样，是各个线程共享的内存区域。Object Class Data(类定义数据)是存储在方法区的，此外，常量、静态变量、JIT编译后的代码也存储在方法区。

运行时常量池：运行时常量池是方法区的一部分。Class 文件中的常量池（编译器生成的各种字面量和符号引用）会在类加载后被放入这个区域。除了在编译期生成的常量，还允许动态生成，例如 String 类的 intern()。这部分常量也会被放入运行时常量池。

直接内存：直接内存（Direct Memory）并不是虚拟机运行时数据区的一部分，也不是Java虚拟机规范中定义的内存区域，但是这部分内存也被频繁地使用，而且也可能导致OutOfMemoryError 异常出现。避免在Java堆和Native堆中来回复制数据。

CMS垃圾收集器

类加载机制和双亲委派模型，以及为什么要实现双亲委派模型

虚拟机调优参数

三、数据结构与算法

链表反转

将当前节点和下一节点保存起来，然后将当前节点反转。

    public ListNode ReverseList(ListNode head) {
        //head为当前节点，如果当前节点为空的话，那就什么也不做，直接返回null
        ListNode pre = null;//pre为当前节点的前一节点
        ListNode next = null;//next为当前节点的下一节点
        //需要pre和next的目的是让当前节点从pre.head.next1.next2变成pre<-head next1.next2
        //即pre让节点可以反转所指方向，但反转之后如果不用next节点保存next1节点的话，此单链表就此断开了
        //所以需要用到pre和next两个节点
        //1.2.3.4.5
        //1<-2<-3 4.5
        //做循环，如果当前节点不为空的话，始终执行此循环，此循环的目的就是让当前节点从指向next到指向pre
        while (head != null) {
            //先用next保存head的下一个节点的信息，保证单链表不会因为失去head节点的原next节点而就此断裂
            next = head.next;
            //保存完next，就可以让head从指向next变成指向pre了
            head.next = pre;
            //head指向pre后，就继续依次反转下一个节点
            //让pre，head，next依次向后移动一个节点，继续下一次的指针反转
            pre = head;
            head = next;
        }
        //如果head为null的时候，pre就为最后一个节点了，但是链表已经反转完毕，pre就是反转后链表的第一个节点
        //直接输出pre就是我们想要得到的反转后的链表
        return pre;
    }

利用递归走到链表的末端，然后再更新每一个节点的next值 ，实现链表的反转。

    public ListNode ReverseList(ListNode head) {
        //如果链表为空或者链表中只有一个元素 
        if (head == null || head.next == null) return head;
        //先递归找到到链表的末端结点，从后依次反转整个链表
        ListNode reverseHead = ReverseList(head.next);
        //再将当前节点设置为后面节点的后续节点 
        head.next.next = head;
        head.next = null;
        return reverseHead;
    }

跳楼梯

package Recursion;

/**
 * 一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
 */
public class Solution04 {
    public static void main(String[] args) {
        Solution04 solution04 = new Solution04();
        System.out.println(solution04.JumpFloor_2(3));

    }

    /**
     * 直接用递归
     * * 对于第n个台阶来说，只能从n-1或者n-2的台阶跳上来，所以
     * F(n) = F(n-1) + F(n-2)
     * f(1)=1
     * f(2)=2
     *
     * @param target 台阶数
     * @return 跳法
     */
    public int JumpFloor(int target) {
        if (target <= 1) {
            return 1;
        }
        if (target <= 2) {
            return 2;
        } else {
            return JumpFloor(target - 1) + JumpFloor(target - 2);
        }
    }

    /**
     * 用迭代的方法，用两个变量记录f(n-1) f(n-2)
     *
     * @param target 台阶数
     * @return 跳法
     */
    public int JumpFloor_2(int target) {
        int one = 1, two = 2, fN = 0;
        if (target <= 0) {
            return 0;
        } else if (target == 1) {
            return 1;
        } else if (target == 2) {
            return 2;
        } else {
            for (int i = 3; i <= target; i++) {
                fN = one + two;
                one = two;
                two = fN;
            }
            return fN;
        }
    }
}

不用乘法实现乘法

一个字符串找里面是否有重复的字符

数组的最大连续子串和

package Array;

/**
 * 连续子数组的最大和
 * 在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？
 * 例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。(子向量的长度至少是1)
 */

public class Solution01 {
    public static void main(String[] args) {
        int[] arr = {6,-3,-2,7,-15,1,2,2};
        System.out.println(FindGreatestSumOfSubArray(arr));
    }
    public static int FindGreatestSumOfSubArray(int[] array) {
        if(array.length==0)
            return 0;
        int sum = array[0];//保存每组的和
        int maxSum = array[0];//连续子数组最大和
        //动态规划
        for(int i = 1;i

快排的思想，为什么是O(N)，每次的基准选择哪个

    /**
     * 快速排序
     *
     * @param array
     * @param _left
     * @param _right
     */
    private static void quickSort(int[] array, int _left, int _right) {
        int left = _left;//
        int right = _right;
        int pivot;//基准线
        if (left < right) {
            pivot = array[left];
            while (left != right) {
                //从右往左找到比基准线小的数
                while (left < right && pivot <= array[right]) {
                    right--;
                }
                //将右边比基准线小的数换到左边
                array[left] = array[right];
                //从左往右找到比基准线大的数
                while (left < right && pivot >= array[left]) {
                    left++;
                }
                //将左边比基准线大的数换到右边
                array[right] = array[left];
            }
            //此时left和right指向同一位置
            array[left] = pivot;
            quickSort(array, _left, left - 1);
            quickSort(array, left + 1, _right);
        }
    }

最好情况下时间复杂度最低的是那种排序

分层打印二叉树

package Tree;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

/**
 * 从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。
 * 思路：
 * 按层次输出二叉树
 * 访问根节点，并将根节点入队。
 * 当队列不空的时候，重复以下操作。
 * 1、弹出一个元素。作为当前的根节点。
 * 2、如果根节点有左孩子，访问左孩子，并将左孩子入队。
 * 3、如果根节点有右孩子，访问右孩子，并将右孩子入队。
 */
public class Solution8 {

    public static void main(String[] args) {
        int[] array = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        Solution8 solution8 = new Solution8();
        TreeNode treeNode = solution8.createBinaryTreeByArray(array, 0);
        for (ArrayList list :
                solution8.Print(treeNode)) {
            System.out.println(list);
        }
    }


    /**
     * 层次遍历
     *
     * @param pRoot 根节点
     * @return arrayLists
     */
    ArrayList> Print(TreeNode pRoot) {
        //存放结果
        ArrayList> arrayLists = new ArrayList<>();
        if (pRoot == null) {
            return arrayLists;
        }
        //使用队列，先进先出
        Queue queue = new LinkedList<>();
        //存放每行的列表
        ArrayList arrayList = new ArrayList<>();
        //记录本层打印了多少个
        int start = 0;
        //记录下层打几个
        int end = 1;
        queue.add(pRoot);
        while (!queue.isEmpty()) {
            TreeNode temp = queue.remove();
            //添加到本行的arrayList
            arrayList.add(temp.val);
            start++;
            //每打印一个节点，就把此节点的下一层的左右节点加入队列，并记录下一层要打印的个数
            if (temp.left != null) {
                queue.add(temp.left);
            }
            if (temp.right != null) {
                queue.add(temp.right);
            }
            //判断本层打印是否完成
            if (start == end) {
                //此时的queue中存储的都是下一层的节点，则end即为queue大小
                end = queue.size();
                start = 0;
                //把arrayList添加到结果列表arrayLists中
                arrayLists.add(arrayList);
                //重置arrayList
                arrayList = new ArrayList<>();
            }
        }

        return arrayLists;
    }



    private TreeNode createBinaryTreeByArray(int[] array, int index) {
        TreeNode tn = null;
        if (index < array.length) {
            int value = array[index];
            tn = new TreeNode(value);
            tn.left = createBinaryTreeByArray(array, 2 * index + 1);
            tn.right = createBinaryTreeByArray(array, 2 * index + 2);
            return tn;
        }
        return tn;
    }


    public class TreeNode {
        int val = 0;
        TreeNode left = null;
        TreeNode right = null;

        public TreeNode(int val) {
            this.val = val;
        }
    }
}

非递归方式实现二叉树的层序遍历

• 思路：
• 访问根节点，并将根节点入队。
• 当队列不空的时候，重复以下操作。
• 1、弹出一个元素。作为当前的根节点。
• 2、如果根节点有左孩子，访问左孩子，并将左孩子入队。
• 3、如果根节点有右孩子，访问右孩子，并将右孩子入队。

    public void levelOrder(TreeNode root) {
        //使用队列，先进先出
        Queue queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode temp = queue.poll();
            System.out.print(temp.val + "  ");
            if (temp.left != null) {
                queue.offer(temp.left);
            }
            if (temp.right != null) {
                queue.offer(temp.right);
            }
        }
    }

非递归方式实现二叉树的中序遍历

二叉树后序遍历

如何判断链表有环

剑指Offer-链表中环的入口结点

package LinkedList;

import java.util.HashSet;

public class Solution24 {

    /**
     * 假设x为环前面的路程，a为环入口到相遇点的路程， c为环的长度
     * 当快慢指针相遇的时候： 此时慢指针走的路程为Sslow = x + m * c + a
     * 快指针走的路程为Sfast = x + n * c + a
     * 2 Sslow = Sfast
     * 2 * ( x + m*c + a ) = (x + n *c + a)
     * 从而可以推导出： x = (n - 2 * m )*c - a = (n - 2 *m -1 )*c + c - a
     * 即环前面的路程 = 数个环的长度（为可能为0） + c - a
     * 什么是c - a？这是相遇点后，环后面部分的路程。
     * 所以，我们可以让一个指针从起点A开始走，让一个指针从相遇点B开始继续往后走， 2个指针速度一样，
     * 那么，当从原点的指针走到环入口点的时候（此时刚好走了x） 从相遇点开始走的那个指针也一定刚好到达环入口点。
     * 所以两者会相遇，且恰好相遇在环的入口点。
     * 时间复杂度：O(n)
     * 空间复杂度：O(1)
     *
     * @param pHead
     * @return
     */
    public ListNode EntryNodeOfLoop_2(ListNode pHead) {
        if (pHead == null || pHead.next == null || pHead.next.next == null)
            return null;
        ListNode fast = pHead.next.next;
        ListNode slow = pHead.next;
        //先判断有没有环
        while (fast != slow) {
            if (fast.next != null && fast.next.next != null) {
                fast = fast.next.next;
                slow = slow.next;
            } else {
                //没有环
                return null;
            }
        }

        fast = pHead;//把fast指向头节点
        //有环
        while (fast != slow) {
            fast = fast.next;
            slow = slow.next;
        }
        return fast;
    }

    /**
     * 利用HashSet元素不能重复
     *
     * @param pHead
     * @return
     */
    public ListNode EntryNodeOfLoop(ListNode pHead) {
        HashSet hashSet = new HashSet<>();
        while (pHead != null) {
            if (!hashSet.add(pHead)) {
                return pHead;
            }
            pHead = pHead.next;
        }
        return null;
    }

    public class ListNode {
        int val;
        ListNode next = null;

        ListNode(int val) {
            this.val = val;
        }
    }
}

冒泡排序，如何优化

排序算法-冒泡排序

    /**
     * 冒泡排序
     *
     * @param array
     */
    private static void bubbleSort(int[] array) {
        if (array == null || array.length == 0 || array.length == 1)
            return;
        for (int i = 0; i < array.length - 1; i++) {
            for (int j = 0; j < array.length - 1 - i; j++) {//注意数组边界
                if (array[j] > array[j + 1]) {
                    int temp = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = temp;
                }
            }
        }
    }
    
    private static void bubbleSort(int[] array) {
        if (array == null || array.length == 0 || array.length == 1)
            return;
        boolean flag = true;//发生了交换就为true, 没发生就为false，第一次判断时必须标志位true
        int k = array.length - 1;
        int pos = 0;//pos变量用来标记循环里最后一次交换的位置
        for (int i = 0; i < array.length - 1; i++) {
            flag = false;//每次开始排序前，都设置flag为未排序过
            for (int j = 0; j < k; j++) {//注意数组边界
                if (array[j] > array[j + 1]) {
                    int temp = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = temp;
                    flag = true;//表示交换过数据;
                    pos = j;
                }
            }
            k = pos;
            //判断标志位是否为false，如果为false，说明后面的元素已经有序，就直接return
            if (flag == false)
                return;
        }
    }

合并两个有序数组

Leetcode#88. Merge Sorted Array（合并两个有序数组）

package Array;

/**
 * 88. Merge Sorted Array（合并两个有序数组）
 * 给定两个有序整数数组 nums1 和 nums2，将 nums2 合并到 nums1 中，使得 num1 成为一个有序数组。
 */
public class Solution88 {
    public static void main(String[] args) {
        Solution88 solution88 = new Solution88();

        solution88.merge();
    }

    /**
     * 从两个数组中的末尾开始进行合并，先找两个数组中较大的移动到正确的位置，将那个移动的位置值向前移动一个位置，再进行同样的操作，直到所有的元素处理完。
     *
     * @param nums1
     * @param m
     * @param nums2
     * @param n
     */
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m - 1;
        int j = n - 1;
        int index = m + n - 1;
        while (i >= 0 && j >= 0) {
            if (nums1[i] > nums2[j]) {
                nums1[index--] = nums1[i--];
            } else {
                nums1[index--] = nums2[j--];
            }
        }
        while (j >= 0) {
            nums1[index--] = nums2[j--];
        }
    }
}

给一串数字，建最大堆，以及建堆的时间复杂度，然后就让手撕堆排序的代码

找两字符串中都存在的元素

四、操作系统

死锁产生的条件

• 互斥：每个资源要么已经分配给了一个进程，要么就是可用的。
• 占有和等待：已经得到了某个资源的进程可以再请求新的资源。
• 不可抢占：已经分配给一个进程的资源不能强制性地被抢占，它只能被占有它的进程显式地释放。
• 环路等待：有两个或者两个以上的进程组成一条环路，该环路中的每个进程都在下一个进程所占有的资源。

产生死锁后如何解决

• 鸵鸟策略
• 死锁检测与死锁恢复
• 死锁预防
• 死锁避免

线程和进程的区别

进程：进程是操作系统资源分配的基本单位。每个进程都有独立的代码和数据空间（进程上下文），进程间的切换会有较大的开销，一个进程包含1–n个线程。

线程：线程是CPU独立调度的基本单位。同一类线程共享代码和数据空间，每个线程有独立的运行栈和程序计数器(PC)，线程切换开销小。

线程和进程的生命周期：新建、就绪、运行、阻塞、死亡

进程间的通信

• 消息传递
  • 管道
  • 消息队列
  • 套接字
• 共享内存

作业调度算法

五、网络

osi，为什么是7层？

OSI七层网络模型	对应网络协议
应用层	HTTP、TFTP、FTP、NFS、WAIS、SMTP
表示层	Telnet、Rlogin、SNMP、Gopher
会话层	SMTP、DNS
传输层	TCP、UDP
网络层	IP、ICMP、ARP、RARP、AKP、UUCP
数据链路层	FDDI、Ethernet、Arpanet、PDN、SLIP、PPP
物理层	IEEE 802.1A、IEEE 802.2到IEEE 802.11

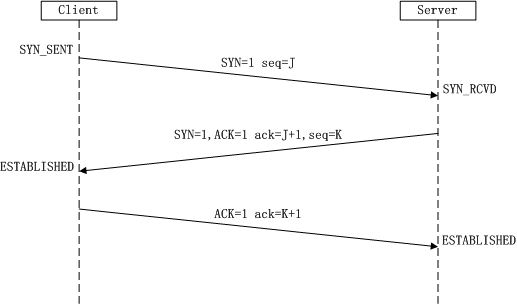
tcp三次握手

所谓三次握手（Three-Way Handshake）即建立TCP连接，就是指建立一个TCP连接时，需要客户端和服务端总共发送3个包以确认连接的建立。整个流程如下图所示：

1. 第一次握手：Client将标志位SYN置为1，随机产生一个值seq=J，并将该数据包发送给Server，Client进入SYN_SENT状态，等待Server确认。
2. 第二次握手：Server收到数据包后由标志位SYN=1知道Client请求建立连接，Server将标志位SYN和ACK都置为1，ack=J+1，随机产生一个值seq=K，并将该数据包发送给Client以确认连接请求，Server进入SYN_RCVD状态。
3. 第三次握手：Client收到确认后，检查ack是否为J+1，ACK是否为1，如果正确则将标志位ACK置为1，ack=K+1，并将该数据包发送给Server，Server检查ack是否为K+1，ACK是否为1，如果正确则连接建立成功，Client和Server进入ESTABLISHED状态，完成三次握手，随后Client与Server之间可以开始传输数据了。

tcp四次挥手

TCP三次握手和四次挥手

为什么三次握手和四次挥手

Server在LISTEN状态下，收到建立连接请求的SYN报文后，可以直接把ACK和SYN放在一个报文里发送给Client。而关闭连接时，当收到对方的FIN报文时，仅仅表示对方不再发送数据了但是还能接收数据，己方也未必全部数据都发送给对方了，所以己方可以立即close，也可以发送一些数据给对方后，再发送FIN报文给对方来表示同意现在关闭连接，因此，己方ACK和FIN一般都会分开发送。

http发送的包里面有什么

TCP/IP五层结构，每次层分别有哪些协议

计算机网络体系结构

TCP和UDP的区别

TCP和UDP的区别

如果网络情况不好，三次握手怎么保证认证

tcp拥塞控制机制，慢开始，拥塞避免，快重传，快恢复

浏览器输入网址按下回车后执行的全过程

域名解析 --> 发起TCP的3次握手 --> 建立TCP连接后发起http请求 --> 服务器响应http请求，浏览器得到html代码 --> 浏览器解析html代码，并请求html代码中的资源（如js、css、图片等） --> 浏览器对页面进行渲染呈现给用户

HTTP与HTTPS区别

session和cookie

六、数据库

对于redis的认识

mysql索引了解

数据库三大范式

解释脏读，幻读，可重复读

redis是单线程还是多线程，分布式锁

单线程

数据库隔离级别，每层级别分别用什么方法实现

• 未提交读（READ UNCOMMITTED）：事务中的修改，即使没有提交，对其它事务也是可见的。最低级别，任何情况都无法保证。
• 提交读（READ COMMITTED）：一个事务只能读取已经提交的事务所做的修改。换句话说，一个事务所做的修改在提交之前对其它事务是不可见的。可避免脏读的发生。
• 可重复读（REPEATABLE READ）：保证在同一个事务中多次读取同样数据的结果是一样的。可避免脏读、不可重复读的发生。
• 可串行化（SERIALIXABLE）：强制事务串行执行。可避免脏读、不可重复读、幻读的发生。

在MySQL数据库中，支持上面四种隔离级别，默认的为REPEATABLE READ(可重复读)。

三级封锁协议,共享锁排它锁，mvcc多版本并发控制协议，间隙锁

b+树和b数的区别，b+数的具体结构

innnodb和myisam的区别，各自的b数索引叶子节点分别存储什么

全文索引，索引什么时候会失效

索引的优化，最左前缀原则

事务的特性

七、设计模式

会那些设计模式

单例模式，工厂模式，代理模式，装饰器模式

八、框架

springboot介绍一下

SpringBoot就是对各种框架的整合，让框架集成在一起更加简单，简化了开发过程、配置过程、部署过程、监控过程。

@SpringBootApplication

aop和ioc理解和原理

IOC:控制反转也叫依赖注入，IOC利用java反射机制。所谓控制反转是指，本来被调用者的实例是有调用者来创建的，这样的缺点是耦合性太强，IOC则是统一交给spring来管理创建，将对象交给容器管理，你只需要在spring配置文件总配置相应的bean，以及设置相关的属性，让spring容器来生成类的实例对象以及管理对象。在spring容器启动的时候，spring会把你在配置文件中配置的bean都初始化好，然后在你需要调用的时候，就把它已经初始化好的那些bean分配给你需要调用这些bean的类。

AOP是对OOP的补充和完善。AOP利用的是代理，分为CGLIB动态代理和JDK动态代理。OOP引入封装、继承和多态性等概念来建立一种对象层次结构。OOP编程中，会有大量的重复代码。而AOP则是将这些与业务无关的重复代码抽取出来，然后再嵌入到业务代码当中。实现AOP的技术，主要分为两大类：一是采用动态代理技术，利用截取消息的方式，对该消息进行装饰，以取代原有对象行为的执行；二是采用静态织入的方式，引入特定的语法创建“方面”，从而使得编译器可以在编译期间织入有关“方面”的代码，属于静态代理。

反射，cglib代理，动态代理，如何实现

springboot的启动流程

spring中bean的生命周期

springmvc执行流程

1. 客户端发送HTTP请求到服务器
2. SpringMVC的核心DispatcherServlet将请求交给HandlerMapping处理
3. HandlerMapping通过查询机制找到处理当前请求的Handler
4. DispatcherServlet将请求交给这个Handler处理
5. Handler处理完成后返回一个ModleAndView对象，这个对象包含视图逻辑名和数据对象
6. 返回的视图逻辑名会通过视图解析器解析成真正的视图，并交给DispatcherServlet处理
7. DispatcherServlet将请求分派给真正的视图对象，并反映到客户端

九、智力题

甲有n个白球，m个黑球，乙有无数个黑球。从甲抽两个球，都是白的，放回甲，一白一黑，从乙拿出黑给甲，都是黑，放回一个给甲。问甲中最后剩下一白一黑的概率