动态规划总结——背包dp(基于LeetCode题目)
题目汇总
这类问题阔以说是笔试最常出现的题目了(线性dp也挺常见,啥最长上升子序列啥啥的)。
这类问题如果不是太难基本上阔以套模板的。
抽象一下
就是有一个收益尽可能大的目标,有一个其他消耗,在允许的消耗范围内使得收益最大。
子问题也很好想,就是某个消耗限制下最大的收益。
这类问题分为01背包,多重背包,完全背包。
01背包就是同个有价值的消耗都只有一个。
多重背包每个有价值的消耗有有限个(可以转换为01背包)。
完全背包就是每个有价值的消耗有无穷个。

这是一个01背包问题。那个数组里的就是消耗。
价值: 就是消耗和为s的最大情况
消耗: 选择数的运算结果
这道题有意思地方在于所有的消耗都得选一种情况(+-)。
dp定义:
因为中间结果有负数的情况用数组的话不方便调整,那使用map吧
dp[n][inx] :当前n个数字内,价值为inx的总数量。
转移方程:
dp[n][inx] = dp[n-1][inx-当前消耗]+dp[n-1][inx-当前消耗]
初始化:
dp[0][nums[0]] += 1;dp[0][-nums[0]] += 1;
hhhhh可想而知的很慢,不过能过
class Solution {
public int findTargetSumWays(int[] nums, int S) {
Map<Bind<Integer>,Integer> map = new HashMap();
int sum1 = Arrays.stream(nums).sum();
map.put(new Bind(0,nums[0]),1);
map.put(new Bind(0,-nums[0]),map.getOrDefault(new Bind(0,-nums[0]),0)+1);
for(int i=1;i<nums.length;i++){
for(int j=sum1;j>=-sum1;j--){
map.put(new Bind(i,j),map.getOrDefault(new Bind(i-1,j-nums[i]),0)+map.getOrDefault(new Bind(i-1,j+nums[i]),0));
}
}
Integer ans = map.get(new Bind(nums.length-1,S));
return ans==null?0:ans;
}
}
class Bind<T>{
T t1;
T t2;
public Bind(T t1,T t2){
this.t1 = t1;
this.t2 = t2;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Bind<?> bind = (Bind<?>) o;
return Objects.equals(t1, bind.t1) &&
Objects.equals(t2, bind.t2);
}
@Override
public int hashCode() {
return Objects.hash(t1, t2);
}
}
用数组来搞其实也不麻烦啦,就多几个边界判断而已,将0点往前移动sum1即可。
class Solution {
public int findTargetSumWays(int[] nums, int S) {
int sum1 = Arrays.stream(nums).sum();
if((S>=0&&sum1<S)||(S<0&&-sum1>S)){
return 0;
}
int[][] dp = new int[nums.length][sum1*2+1];
dp[0][nums[0]+sum1] += 1;
dp[0][-nums[0]+sum1] += 1;
//System.out.println(Arrays.toString(dp[0]));
for(int i=1;i<nums.length;i++){
for(int j=sum1+sum1;j>=0;j--){
if(j+nums[i]<dp[0].length){
dp[i][j] += dp[i-1][j+nums[i]];
}
if(j-nums[i]>=0){
dp[i][j] += dp[i-1][j-nums[i]];
}
}
//System.out.println(Arrays.toString(dp[i]));
}
return dp[nums.length-1][S+sum1];
}
}
还可以用滚动数组压缩一下空间。
想要知道m个1,n个0至多能匹配多少个串子。
可以逆向考虑要匹配完全部串至少需要多少个0和1.
再取出m个1和n个0时的情况即可。
定义:
dp[i][j] :i个0,j个1至多可以匹配多少个串。
转移方程:
若某串有x个0,y个1
dp[i][j] =
if(i>=x&&y>=j)
max(dp[i-x][j-y]+1,dp[i][j]);
else
dp[i][j];
初始化:
0个0和0个1的情况下只能匹配0个串。
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m+1][n+1];
for(String s:strs){
int zero = count(s,'0');
int one = count(s,'1');
for(int i=m;i>=zero;i--){
for(int j=n;j>=one;j--){
dp[i][j] = Math.max(dp[i-zero][j-one]+1,dp[i][j]);
}
}
}
return dp[m][n];
}
private int count(String s,char t){
return Arrays.stream(s.split("")).
map(x->x.charAt(0)).
mapToInt(x->x==t?1:0).sum();
}
}
定义:
dp[i] : i元最少可以由几枚硬币兑换
转移方程:
dp[i] = min(dp[i-coin[k]]+1,dp[i][j]);
初始化:
因为是求最少的数量所以初始化为一个绝对大于真实数量的值即可
class Solution {
public static int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];
Arrays.fill(dp,amount+1);
dp[0] = 0;
for(int i=1;i<=amount;i++){
for(int j=0;j<coins.length;j++){
if(coins[j]<=i){
dp[i] = Math.min(dp[i-coins[j]]+1,dp[i]);
}
}
}
return dp[amount]==amount+1?-1:dp[amount];
}
}
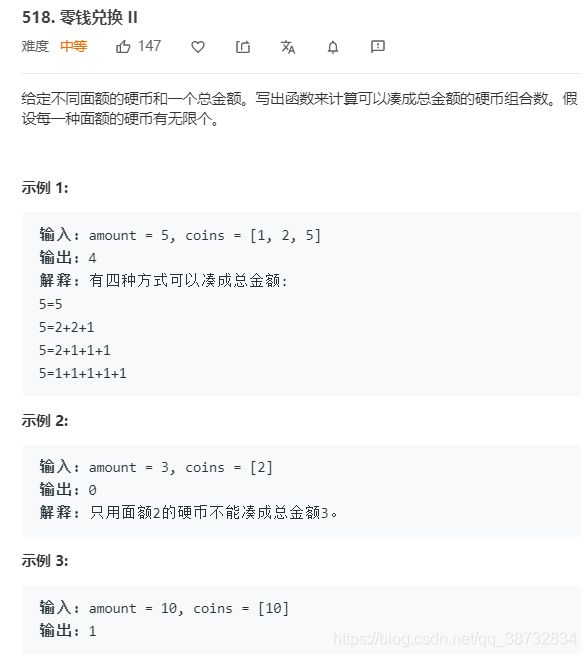
这个问题变成了有几种兑换方式。其实还是那么回事嘛
定义:
dp[i]:i元金额下有几种兑换方式
转移方程:
dp[i] += dp[i-coins[j]]
初始化:
dp[0]=1;0元只有一种啥也不拿的方式
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
dp[0] =1;
for(int j=0;j<coins.length;j++){
for(int i= coins[j];i<=amount;i++){
dp[i] += dp[i-coins[j]];
}
}
return dp[amount];
}
}
之前有想过一下循环嵌套的顺序,一个思考方向是将不能重复的循环放于外层,这道题的情况下,两种都能重复,但是得出的结果全全然不一样,不一样的原因是一种是一种是排列数也就是说每一步都可以在硬币中选择(内层循环为硬币的选择),另一种一种则是组合数(这些硬币在不同大小的金额限制下重复选择过多次,所以也不存在什么在外层不能重复用了),一次将它能在的位置都写进去,不关心顺序只在乎能不能用到(每个金额对于每个硬币只会出现一次自然就不会重复计数)。

这道题的意思可以转换为选定x个数能够组合成的和(sum1)里有没有正好能是总数组和的1/2的。
定义:
dp[i][j]:i个数字中是否有组成和为j的数
状态转移方程
dp[i][j] = dp[i-1][j-nums[k]]||dp[i][j]
初始化:
dp[0][0] =true;//0个数字结果肯定为0啊
class Solution {
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
if((sum&1)==1){
return false;
}
int h = (sum>>1)+1;
boolean[][] dp = new boolean[nums.length][h];
dp[0][0] = true;
if(nums[0]<h){
dp[0][nums[0]] = true;
}
for(int i =1;i<nums.length;i++){
for(int j= 0;j<h;j++){
dp[i][j] = dp[i-1][j];
if(j>=nums[i]){
dp[i][j] = dp[i][j]||dp[i-1][j-nums[i]];
}
if(dp[i][h-1]){
return true;
}
}
}
return false;
}
}